Answer:
Given:
Find:
Probability of rain in days and what happen as
Solution:
Consider the experiment that generates today's weather. Hence possible outcomes can be divided into 2 disjoint events: rain and no rain (A day can either be rainy or not, hence this division contains all possible outcomes).
Hence
Now using the law of total probability, we write
|
| (1) |
But
Note: To proof the above, we can utilize a simple state transition diagram as follows
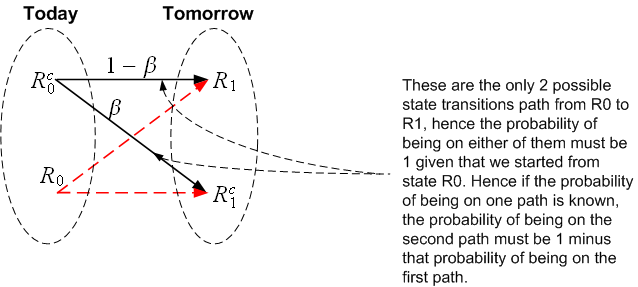
Now, substitute (2) into (1) and given that and
and
, then (1)
becomes
|
| (3) |
Now we can recursively apply the above to find probability of rain on the day after tomorrow. Let
and
, hence the above (1) becomes
|
| (4) |
Now using (3) for and given that
(This probability does not change, since we are
told only today's weather is relevant), and given that
and that
,
then (4) becomes
We see that as we continue with the above process, terms will be generated with the form
(something) and (something)
, where the powers
are getting larger and larger as
gets
larger. But since
, hence all these terms go to zero. So we only need to look at the terms which do not
contain a product of
and product of
Hence the above reduces
There is a pattern here, to see it more clearly, I generated more for
using a small
piece of code and removed all terms of higher powers of
as described above, and I get the following
table
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
Hence the pattern can be seen as the following
Where for even
and
for odd
, and
means to round to nearest lower integer
and
means to round upper.
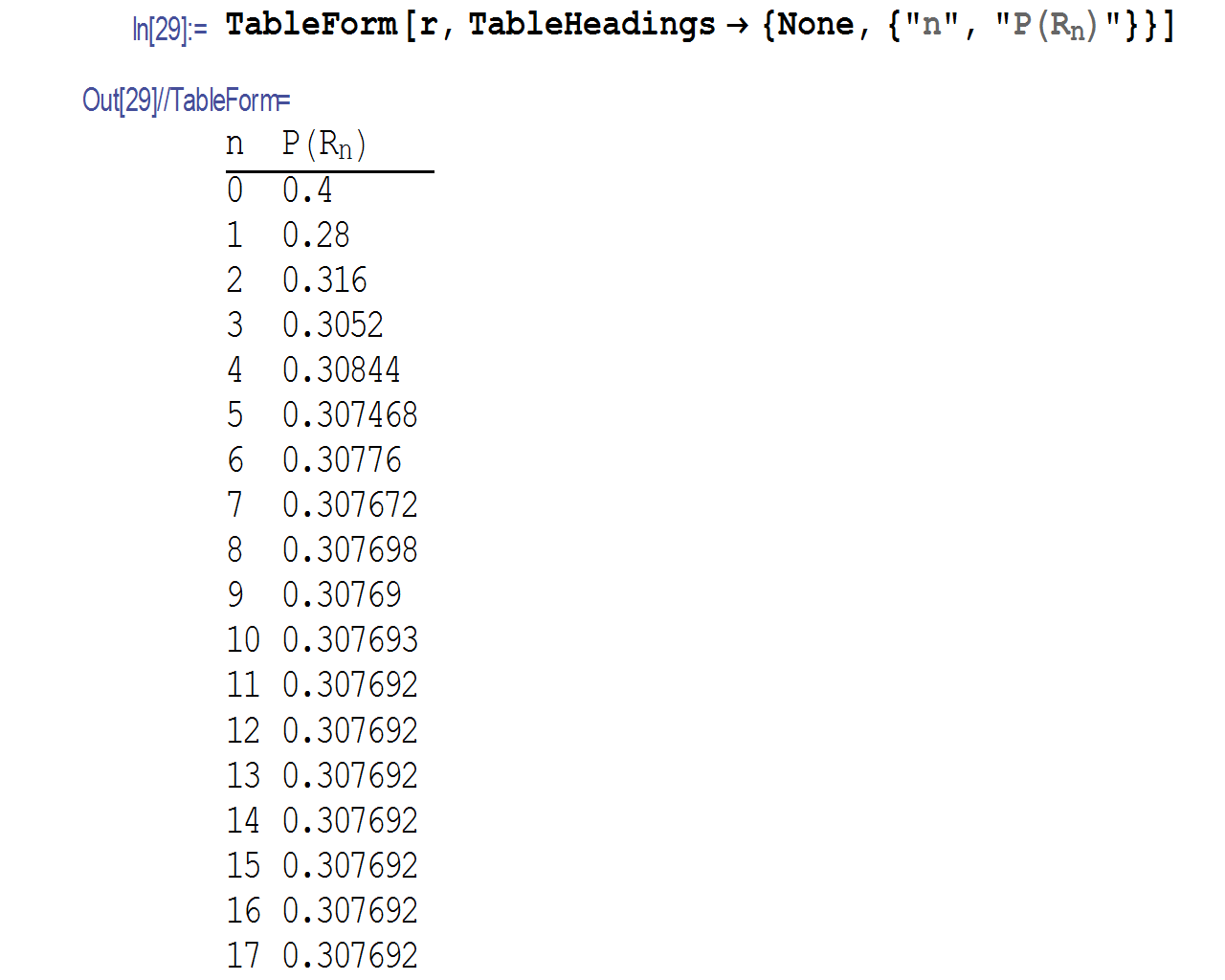
The above is valid for very large .
As will reach a fixed value (I first though it will always go to 1, but that turned out not
to be the case). I could not find an exact expression for
as
, but I wrote a small program
which simulates the above, and generates a table. Here is a table for few values as
gets large, these are all
for
notice that
fluctuates up and down from one day to the next as it converges
to its limit.
Given: Conditional probabilities exist
Show:
Solution:
Since Conditional probabilities exist, then we know that the following is true
Let and
hence the above becomes
Now apply the same idea to the last term above. In other words, we write
We repeat the process until we obtain
Hence, putting all the above together, we write
The above is what is required to show (terms are just rewritten is reverse order from the problem statement, rearranging, we obtain
QED

Given:
Axioms of probability:
Show that
Solution:
There are 4 possible cases.
Case 1: If are disjoint then
by set theory. Now apply the probability operator on
both sides we obtain that
Now, by Axiom 3, hence the above becomes
Case 2: If then
by set theory. Now apply the probability operator on both sides we
obtain that
But since
and so
by axiom 2. Hence the above
becomes
|
| (0) |
Case 3: This is the same as case 2, just exchange and
case 4: Since, by set theory
Then apply Probability operator on both sides
But by set theory is disjoint from
, then by axiom 3 the above becomes
|
| (1) |
Similarly, by set theory
Then apply Probability operator on both sides
But is disjoint from
, by set theory, then by axiom 3 the above becomes
|
| (2) |
Now by set theory
Apply the probability operator on the above
But and
are disjoint by set theory, then above can be written using axiom 3
as
|
| (3) |
Add (1)+(2)
subtract the above from (3)
Cancel terms (Arithmetic)
or (algebra)
Since is an event in
then
by axiom 2, hence the above can be written
as
|
| (4) |
conclusion: We have looked at all 4 possible cases, and found that or
, hence
Note: I tried, really tried, to find a method which would require me to use the hint given in the problem
that if , then
but I did not need to use such a relationship in the above. But I still
show a proof for this identity below
Given: , Show
proof:
by set theory
by applying probability to each side.
But are disjoint by set theory, hence
by axiom 3.
Hence , or
But by axiom 2, , hence
, QED
Given: binomial r.v., i.e.
Find the mode. This is the value
for
which
is maximum
The mode is where is maximum. Consider 2 terms, when
, and
, hence
will be increasing when
But
Hence
so is getting larger when
or
So as long as , pmf is increasing. Since
is an integer, then we need the largest integer such
that it is
, hence

Given:
members are affected independently
Find: probability 2 individuals are affected in population of size 100,000
part(a)
In Binomial random variable we ask: How many are infected in a trial of length given that the
probability of being infected in each trial to be
Here we view each trial as testing an individual.
Consider it a 'hit' if the individual is infected. The number of trials is
, which is
, and
.
Therefore, how many are infected in population of 100000
Hence the probability of getting hits is, using binomial r.v. is (
in this case)
or numerically
(b)Using Poisson r.v. Poisson is a generalization of Binomial. X is the number of successes in infinite number
of trials, but with the probability of success in each one trial going to zero in such a way that .We
compute
Hence here how many are infected as
gets very large and
, the probability of infection in each
individual goes very small in such a way to keep
fixed at a parameter
. Since here
is large and
is
small, we approximate binomial to Poisson using
Hence
ps. computing a numerical value for the above, shows that using Binomial model, we obtain

and using Poisson model
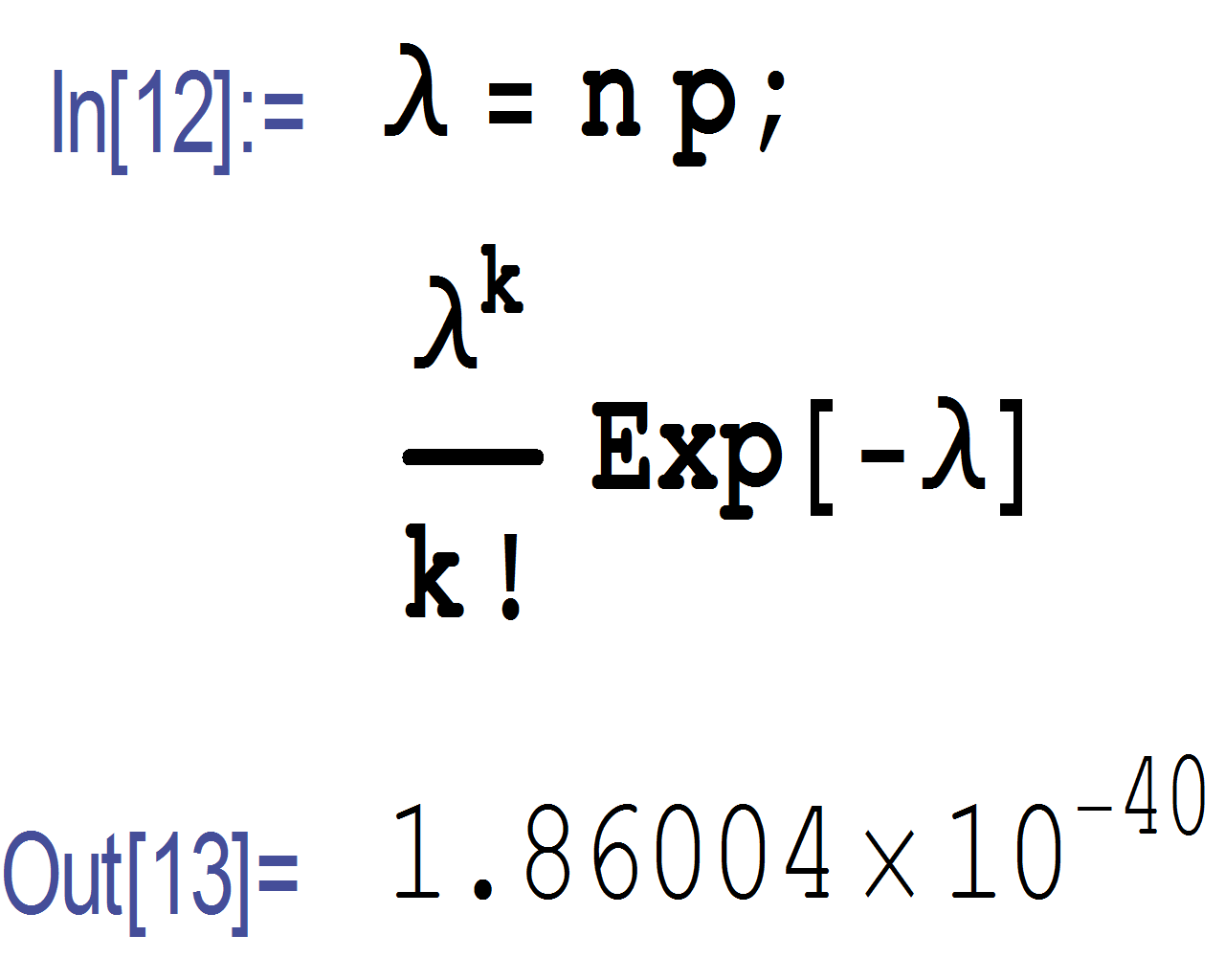
I am not sure, these are such small values, this means there is almost no chance of finding 2 individuals infected in a population of 100,000? I would have expected to see a much higher probability than the above. I do not see what I am doing wrong if anything.