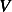 be the space of continuously differentiable functions
be the space of continuously differentiable functions 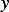 such that
such that 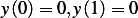 . On this space
consider the functional
. On this space
consider the functional
Let 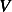 be the space of continuously differentiable functions
be the space of continuously differentiable functions 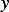 such that
such that 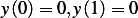 . On this space
consider the functional
. On this space
consider the functional
![∫ 1
J (y) = [y′(x)]2+ q[y(x)]2− 2fy(x) dx
0](in5x.png)
where 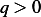 and
and 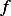 are given constants.
are given constants.
(a) Show that  achieves a minimum at
achieves a minimum at  iff
iff
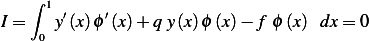
for all 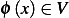
(b)Show that if 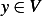 is twice continuously differentiable and satisfies this optimality condition then
is twice continuously differentiable and satisfies this optimality condition then 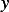 satisfies the differential equation
satisfies the differential equation 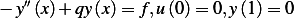
(c)Conversely show that if 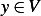 is twice continuously differentiable, and satisfies the differential equation
above, then
is twice continuously differentiable, and satisfies the differential equation
above, then 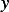 satisfies the optimality condition of part (a)
satisfies the optimality condition of part (a)
.
Let ![1
A = {y∈ C [0,1],y(0)= y(1)= 0}](in17x.png) , and let
, and let ![1
Ay = {ϕ ∈ C [0,1],ϕ (0)= ϕ (1 )= 0}](in18x.png) . The set
. The set 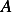 is called
the set of admissible functions (from which the function which will minimize the functional will be found),
and
is called
the set of admissible functions (from which the function which will minimize the functional will be found),
and 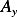 is called the set of admissible directions. We require also that
is called the set of admissible directions. We require also that 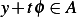 where
where 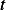 is some small
scalar.
is some small
scalar.
Since this is an IFF, then we need to show the forward and the backward case. Start with the forwards case:
Given: 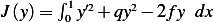 show that
show that
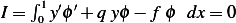 then
then 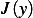 is minimum
is minimum Consider
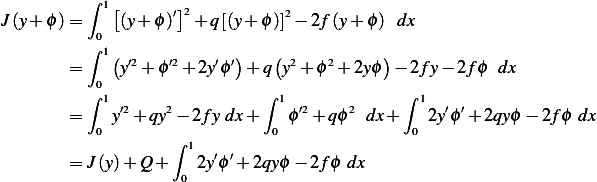
Where 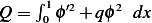
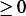 since
since 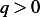 and the other functions are squared. Hence this
implies from the above that if
and the other functions are squared. Hence this
implies from the above that if 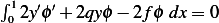 then
then 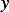 is a minimizer of
is a minimizer of 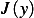 . In other
words
. In other
words
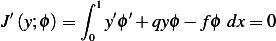
(This is because any change from 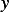 along any of the admissible directions
along any of the admissible directions 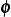 will result in a functional
will result in a functional
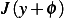 which is larger than it was at
which is larger than it was at 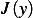 ).
).
Now to show the backward case:
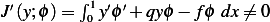 then
then 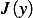 is not a minimum.
is not a minimum. Assume for some 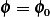 we have
we have 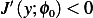
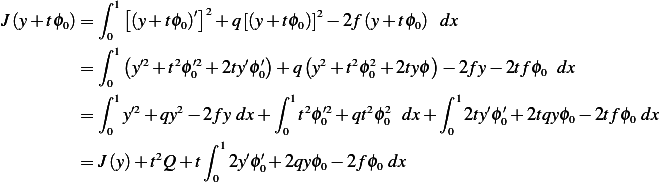
Where 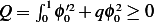 .Hence we have
.Hence we have
![[ ∫ 1 ′ ′ ]
J(y+ tϕ0)= J(y)+ t 2 y ϕ0+ qyϕ0− fϕ0 dx + tQ
0](in44x.png)
Now, no matter how large 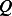 is, we can make
is, we can make 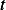 small enough so that
small enough so that 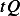 is smaller than the absolute
value of
is smaller than the absolute
value of 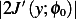 .
.  But since
But since 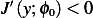 , then
, then ![[ ∫ ]
2 10 y′ϕ′0+ qyϕ0− fϕ0 dx + tQ](in51x.png) will be a
negative quantity. Hence, since
will be a
negative quantity. Hence, since 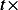 negative quantity is also negative quantity, then we conclude
that
negative quantity is also negative quantity, then we conclude
that
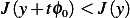
Hence 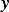 is not a minimizer of
is not a minimizer of 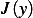 . So no matter which
. So no matter which 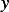 we hope it is our minimum, we can find an
admissible direction
we hope it is our minimum, we can find an
admissible direction 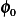 such that if move very slightly away from this
such that if move very slightly away from this 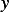 in this admissible direction, we find
that
in this admissible direction, we find
that 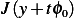 is smaller (this will always be the case if
is smaller (this will always be the case if 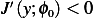 )
)
Given ![y ∈ C2[0,1]](in61x.png) , and
, and 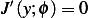 for all admissible directions
for all admissible directions 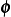 . Show that
. Show that 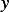 satisfies the differential
equation
satisfies the differential
equation 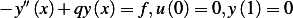
Since 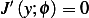 , in other words
, in other words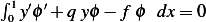 . Then now we do integration by
parts.
. Then now we do integration by
parts.
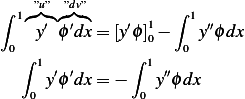
Since  Now substitute the above back into
Now substitute the above back into 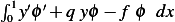 and take
and take 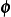 as
common factor, we obtain
as
common factor, we obtain
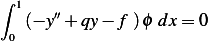
Now we apply the fundamental theory of variational calculus (which Lemma 3.13 is special case) and
argue that since 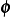 is arbitrary admissible direction, then for the above to be zero for every
is arbitrary admissible direction, then for the above to be zero for every 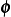 , we must
have
, we must
have
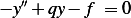
or
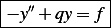
Given ![y ∈ C2[0,1]](in78x.png) and
and 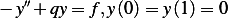 show that
show that 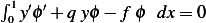
Let 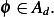 Now
Now
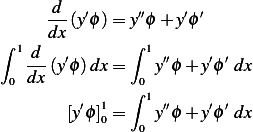
But ![[y′ϕ]1= 0
0](in83x.png) since
since 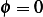 at both ends. Hence the above becomes
at both ends. Hence the above becomes
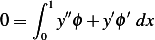
But 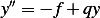 since
since 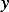 satisfies the differential equation. Hence the above becomes
satisfies the differential equation. Hence the above becomes
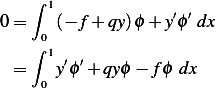
Which is the optimality condition (weak form) of part (a) we are asked to show.