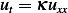 of the form
of the form 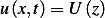 where
where 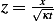
problem:
Find all solutions to the heat equation 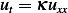 of the form
of the form 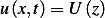 where
where 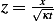
answer:
We have that 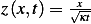 , hence
, hence 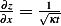 and
and 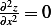 and
and 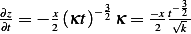
Now
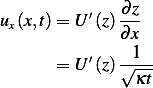
and
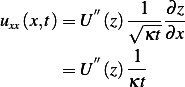
and
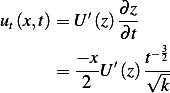
Plug in the above expressions into the PDE we obtain
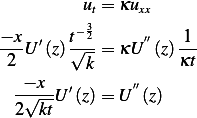
But 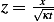 , hence the above becomes
, hence the above becomes
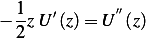
or
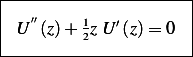
Let 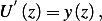 hence the above becomes
hence the above becomes
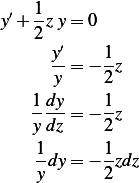
Integrate both sides
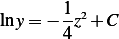
Hence
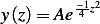
But since 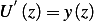 , then
, then
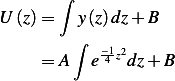
I think now I need to write the above in terms of 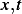 again. Fix time, and change
again. Fix time, and change 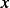 and so we have
and so we have
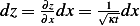 and the above integral becomes
and the above integral becomes
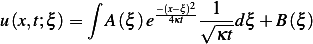
for any  location along the space dimension
location along the space dimension 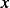 , where
, where 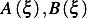 are functions that depend on the
value
are functions that depend on the
value 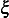
problem:
Use the energy method to prove the uniqueness for the problem
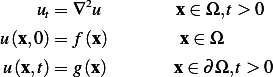
Solution
First note that 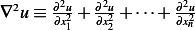 i.e. the Laplacian.
i.e. the Laplacian.
Proof by contradiction. Assume there is no unique solution. Let 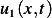 and
and 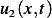 be 2
different solutions to the above PDE. Let
be 2
different solutions to the above PDE. Let 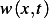 be the difference between these 2 solutions. i.e.
be the difference between these 2 solutions. i.e.
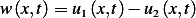 , hence
, hence 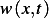 must satisfy the following conditions: it must be zero at the
boundaries
must satisfy the following conditions: it must be zero at the
boundaries 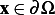 for all time, and also it must be zero inside
for all time, and also it must be zero inside  initially. Hence
initially. Hence

Now if we can show that 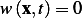 for
for 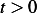 inside
inside  , then this would imply that
, then this would imply that 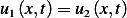 ,
showing a contradiction, hence completing the proof.
,
showing a contradiction, hence completing the proof.
i.e. we need to show that 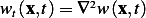 yields a solution
yields a solution 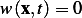 for
for 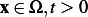
Using the energy argument, we write
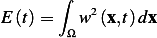
First we note that 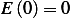 since
since 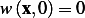 from the initial conditions above.
from the initial conditions above.
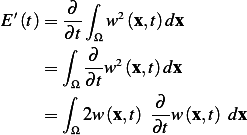
But 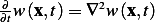 from the PDE itself, hence the above becomes
from the PDE itself, hence the above becomes
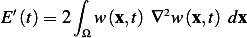 | (1) |
But from Green first identity which states the following
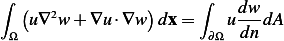
Replace  by
by 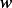 in the above, we obtain
in the above, we obtain
Comparing (1) and (2) we see that LHS of (2) is 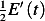 Hence the above become
Hence the above become
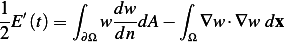
But 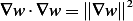 , so the above becomes
, so the above becomes
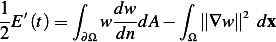
But 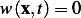 on
on 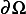 for
for 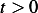 , since this is the boundary conditions. Hence the above
becomes
, since this is the boundary conditions. Hence the above
becomes
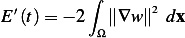
Therefore we showed that 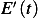 is
is 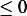 since
since 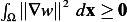
So energy inside  is nonincreasing with time. But since
is nonincreasing with time. But since 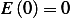 then
then 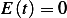 (since energy can not
be negative, this is the only choice left).
(since energy can not
be negative, this is the only choice left).
Therefore, from 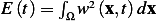 , we conclude that
, we conclude that 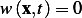 everywhere in
everywhere in  for
for 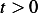 since
since
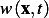 is continuous in both its arguments.
is continuous in both its arguments.
Hence we conclude since 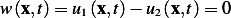 then
then 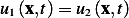 , then the PDE solution is
unique.
, then the PDE solution is
unique.
problem:
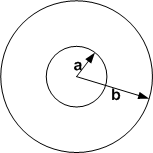
In absence of sources derive the diffusion equation for radial motion in the plane 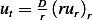 from first
principles. That is, take an arbitrary domain between circles
from first
principles. That is, take an arbitrary domain between circles 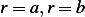 and apply conservation law for the
density
and apply conservation law for the
density 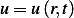 assuming the flux is
assuming the flux is 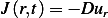 . Assume no sources.
. Assume no sources.
Answer:
First note that the density 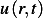 is measured in quantity per unit volume.
is measured in quantity per unit volume.
Consider a cross sectional area through circle 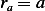 . This area is
. This area is 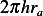 where
where 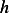 is the width of the
strip.
is the width of the
strip.
Let 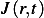 be the flux at
be the flux at  at time
at time 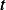 , measured in quantity per unit area per unit time.
, measured in quantity per unit area per unit time.
Hence amount  that passes though cross sectional area at
that passes though cross sectional area at 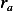 , per unit time, is
, per unit time, is 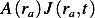 where
where
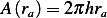
Similarly, amount  that passes though cross sectional area at
that passes though cross sectional area at 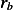 , per unit time, is
, per unit time, is 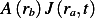 where
where
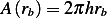
Hence the net amount that flows, per unit time, between 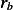 and
and 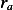 is
is 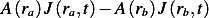
Since there is no source nor sink inside this region, then the above equal the rate at which the amount  itself changes between
itself changes between 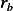 and
and 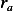 , which is
, which is 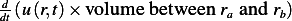 .
.
Hence we have
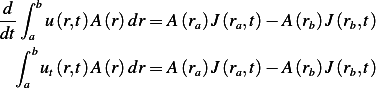
Apply fundamental theorem of calculus on the RHS above where 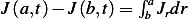 hence the above
becomes
hence the above
becomes
![∫ b ∫ a
ut(r,t)A (r)dr = ∂--[A (r)J (r,t)]dr
a b ∂r](ma106x.png)
But 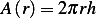 so the above becomes
so the above becomes
![∫ ∫
bu (r,t)rdr = a∂--[rJ(r,t)]dr
a t b ∂r](ma108x.png)
Changing the limits on the integral in the RHS above to make it match the LHS, we obtain
![∫ ∫
bu (r,t)rdr = − b∂--[rJ(r,t)]dr
a t a ∂r](ma109x.png)
Because the above holds for all intervals of integration and the functions involved are continuous, then we can remove the integrals and just write
![-∂-
ut(r,t)r = − ∂r [rJ(r,t)]](ma110x.png)
Now assuming diffusion model for the flux, i.e. 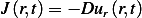 , then the above becomes
, then the above becomes
![∂--
ut(r,t)r = D ∂r [rur(r,t)]](ma112x.png)
Hence
![|-------------|
| D |
| ut = r [rur]r|
---------------](ma113x.png)