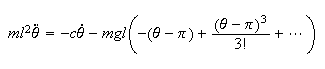
HW1, MAE 200A. Fall 2005. UCI
Nasser Abbasi
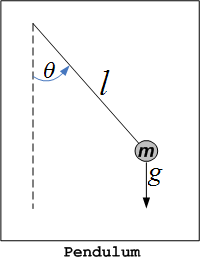
Given this simple pendulum, compute the equilibrium points and determine the linearized dynamics at each equilibrium point

Answer
part(1)
The system equation is given by
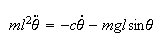
Since this is a second order ODE, there are 2 state variables. Convert this to state space formulation:
Let
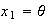 and
and
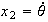 ,
hence
,
hence
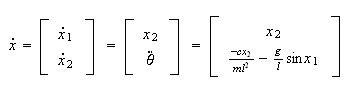
At the equilibrium points we must
have,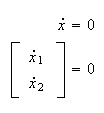
Hence we obtain 2 equations
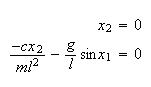
Solving these equations, we obtain
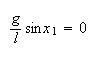 or
or
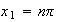 for
for
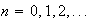
Since the period is
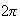 ,
then
,
then
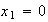 or
or
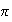 ,
but
,
but
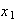 is state variable that represents the angle
is state variable that represents the angle
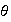 hence
hence
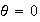 and
and
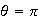
note: equilibrium at
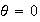 is stable, while at
is stable, while at
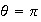 is unstable.
is unstable.
part(2)
starting with the nonlinear system equation
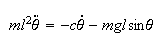
Near the equilibrium points, we express the nonlinear term in taylor series.
Suppose the penulium is at angle
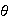 near the angle
near the angle
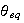 so it is a distance
so it is a distance
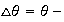
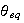
Hence now
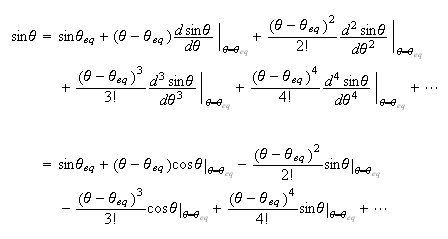
For the first equilibrium point,
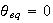 so the above becomes
so the above becomes
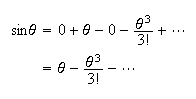
For the first equilibrium point,
 so equation (1) becomes
so equation (1) becomes
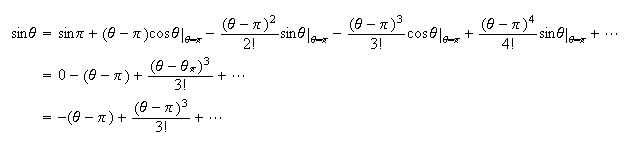
Hence near
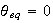 ,
the linearized system equation is
,
the linearized system equation is
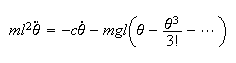
and near
 the system equation is
the system equation is