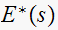 is the Laplace transform of
is the Laplace transform of
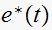 ,
where
,
where
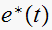 which is the time domain representation of the input signal
which is the time domain representation of the input signal
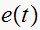 after passing though an ideal sampler.
after passing though an ideal sampler.
HW3, MAE 171. Spring 2005. UCI
Nasser Abbasi
Give the definition of the starred transform.
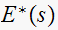 is the Laplace transform of
is the Laplace transform of
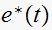 ,
where
,
where
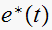 which is the time domain representation of the input signal
which is the time domain representation of the input signal
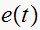 after passing though an ideal sampler.
after passing though an ideal sampler.
Mathematically,
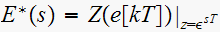 where
where
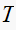 is the sampling period, and
is the sampling period, and
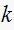 is the sample number and
is the sample number and
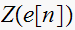 is the
is the
 transform the sequence
transform the sequence
![$e\left[ n\right] $](graphics/hw3__10.gif) .
.
Given the standard definition of the
 transform, then we can now write
transform, then we can now write
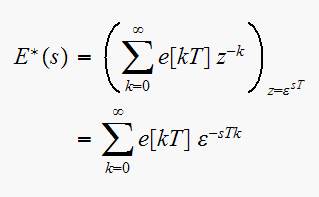
Give the definition of the
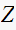 transform.
transform.
Given a sequence
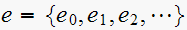 ,
then the one sided
,
then the one sided
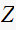 transform of
transform of
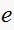 is defined as
is defined as
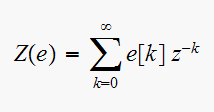
Here we assumed that the number sequence
 has its first element at index
has its first element at index
 .
i.e.
.
i.e.
 for
for
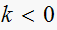
For a function
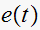 derive a relationship between its starred transform
derive a relationship between its starred transform
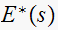 and its
and its
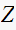 transform
transform

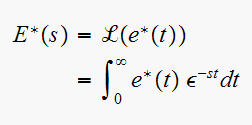
but
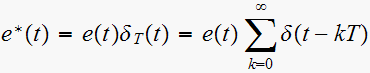
Hence (1) becomes
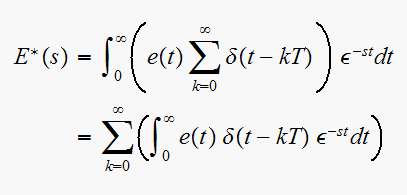
But given the property that
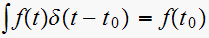 , then
, then
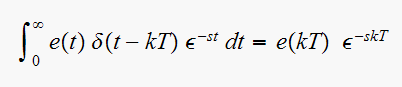 and (2) can be now be written as
and (2) can be now be written as
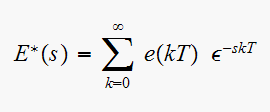
Now, given the one-sided definition of the Z transform of sequence
 as
as
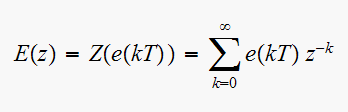 then
by comparing (3) and (4) we see that (3) can be be written as
then
by comparing (3) and (4) we see that (3) can be be written as
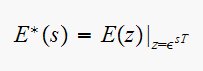
Which is the required relation to show.
Find the starred transform for
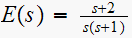
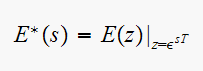
so need to first find the Z transform of
![$e\left[ kT\right] $](graphics/hw3__38.gif) , the discrete time representation of the ideal sampled version of
, the discrete time representation of the ideal sampled version of
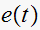
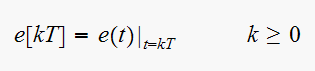
so we need to first find
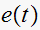
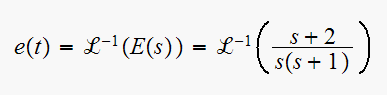
Use partial fraction to find the inverse Laplace transform.
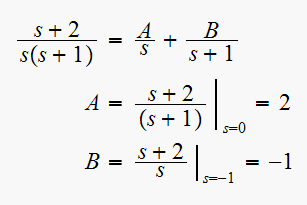
Hence
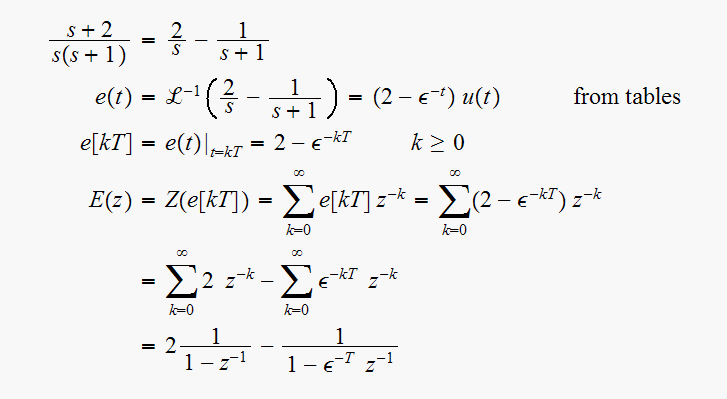
ROC is
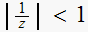 and
and
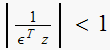
Hence,
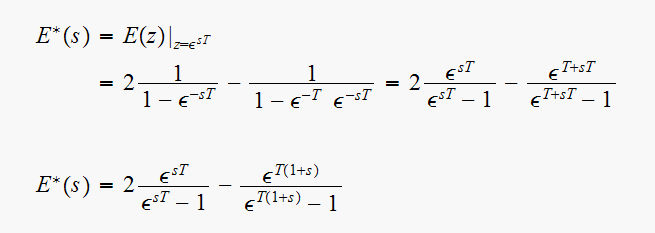
Find the starred transform for
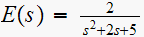
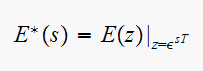
so need to first find the Z transform of
![$e\left[ kT\right] $](graphics/hw3__50.gif) , the discrete time representation of the ideal sampled version of
, the discrete time representation of the ideal sampled version of
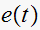
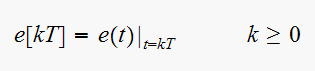
so we need to first find
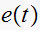
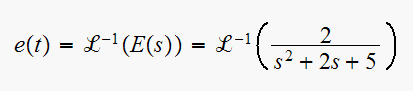
roots of denominator are
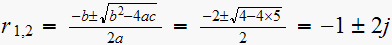
Let
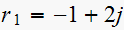 ,
and
,
and
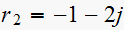 ,
so now
,
so now
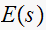 can be written as
can be written as
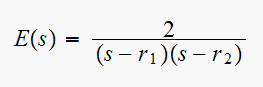
Use partial fraction to find the inverse Laplace transform.
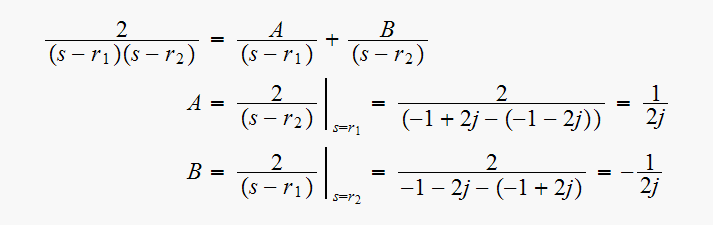
Hence
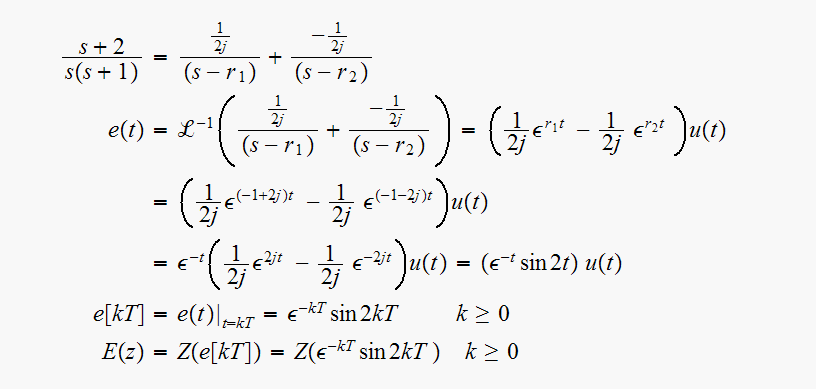
From Tables,
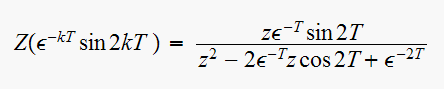
Hence
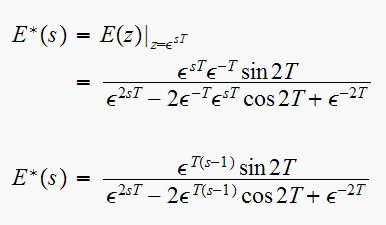
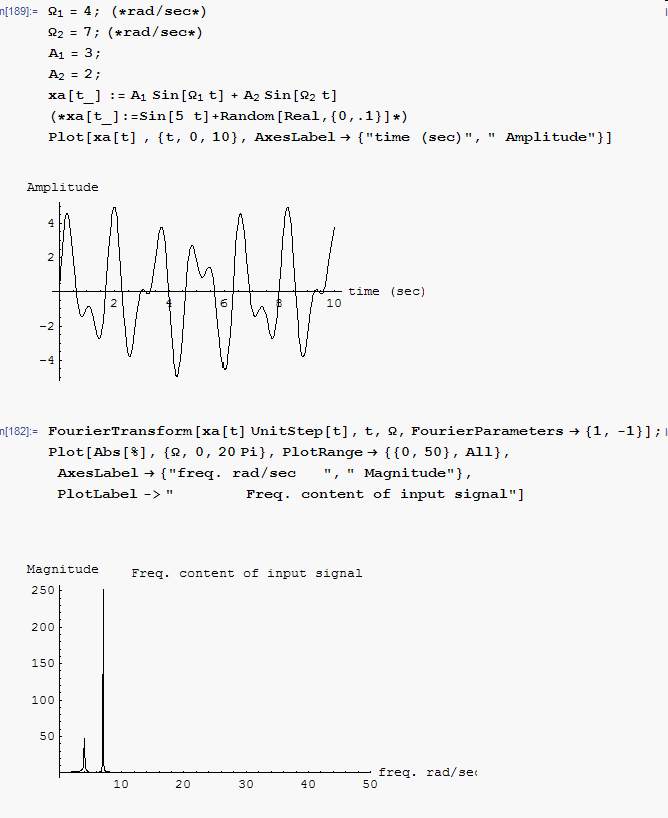
Given the signal
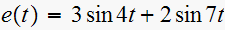
List all frequencies less than
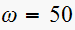 rad/sec that are present in
rad/sec that are present in
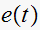
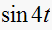 contains a frequency of
contains a frequency of
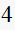 rad/sec.
rad/sec.
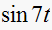 contains a frequency of
contains a frequency of
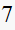 rad/sec.
rad/sec.
Hence the answer is
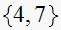 rad/sec
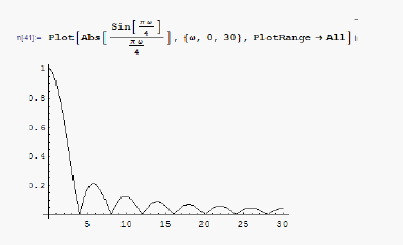
rad/secTo illustrate, this is a small Mathematica script.
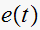 is sampled at
is sampled at
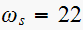 rad/sec. List all frequencies present in
rad/sec. List all frequencies present in
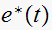 less than
less than
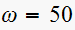 rad/sec.
rad/sec.
The frequency spectrum of the sampled signal will contain frequencies that are
centered around multiples of
Hence the list of generated frequencies are
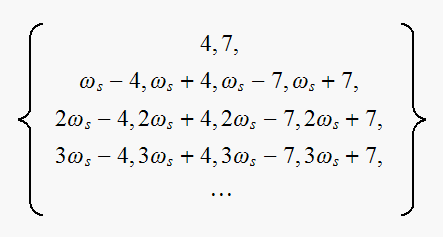
substitute for
 we get
we get
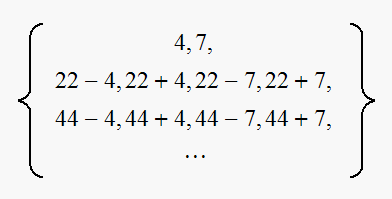
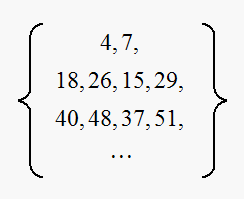
Sort and consider only frequencies less than
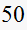 rad/sec, we get
rad/sec, we get
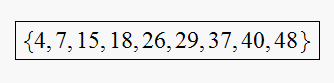
The signal
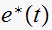 is applied to a ZOH device. List all frequencies present in
is applied to a ZOH device. List all frequencies present in
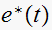 less than
less than
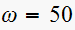 rad/sec.
rad/sec.
Since a ZOH is an LTI device and the input is a set of eigenfunctions, then the output will contain the same set of input frequencies but possibly scaled and phase shifted. Hence this is the same answer as part (b) above.
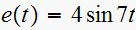 is applied to a samples/ZOH device,
is applied to a samples/ZOH device,
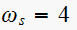 rad/sec.
rad/sec.
what is the frequency component in the output that has the largest amplitude?
This will be the component with the frequency closest to the DC frequency.
Looking at the sequence of frequencies generated, which are
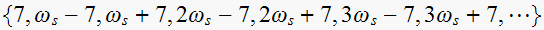
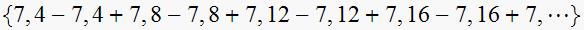
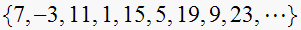
sort, and consider only positive frequencies, we obtain
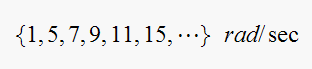
Hence the component with the largest amplitude has a frequency of
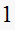 rad/sec
rad/sec
Find amplitude/phase of that component.
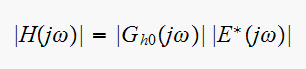
But
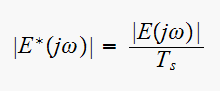 To
find
To
find
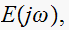 use the relation that
use the relation that
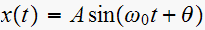 has the Fourier transform
has the Fourier transform
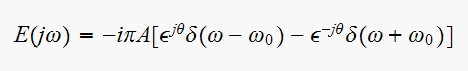 Then,
the Fourier transform of
Then,
the Fourier transform of
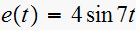 is (where here
is (where here
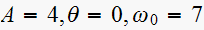 )
)
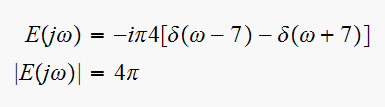 substitute
(3) into (2), then (1) can be written as
substitute
(3) into (2), then (1) can be written as
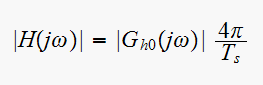 but
but
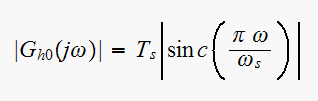 Hence
(4) becomes
Hence
(4) becomes
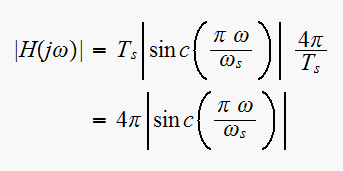 Evaluate
at
Evaluate
at
 rad/sec, and given that
rad/sec, and given that
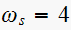 rad/sec, we get
rad/sec, we get
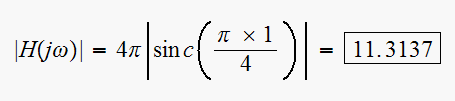 Now
to find the phase of this component.
Now
to find the phase of this component.
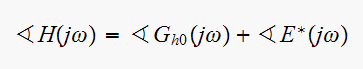 since
since
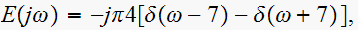 then, since
then, since
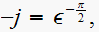 then
then
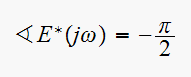 this
is because
this
is because
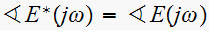 at frequency
at frequency
 rad/sec which is smaller than
rad/sec which is smaller than
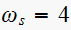 rad/sec, so we are inside the first hub of the sinc function. i.e.
rad/sec, so we are inside the first hub of the sinc function. i.e.
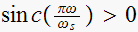 in this case.
in this case.
Now
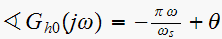 but since
but since
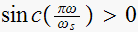 when
when
 ,
then
,
then
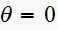 (using equation 3-33 page 105 in book).
(using equation 3-33 page 105 in book).
Hence
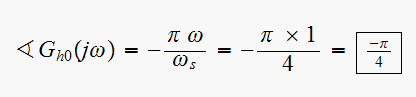
Hence, (5) now becomes
sketch the input signal and the component of part(b) vs. time.
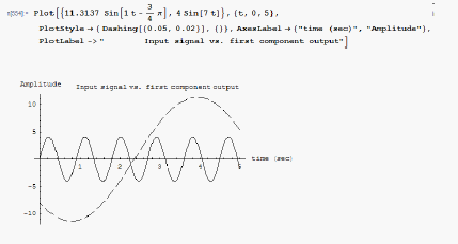
Find the ratio of the amplitude in part(b) to that of the frequency component
in the output at
 rad/sec.
rad/sec.
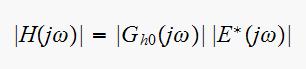
but
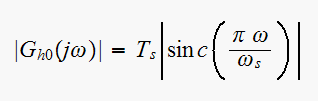
and
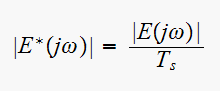
Hence
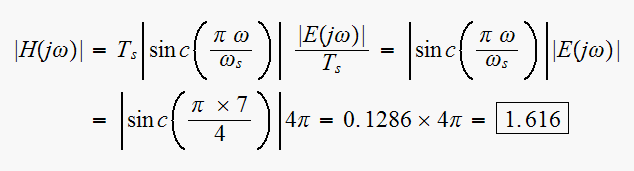
Hence ratio is
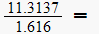
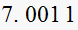
This is expected, as at
 we are in the second hub of the sinc function, which will have much less
amplitude.
we are in the second hub of the sinc function, which will have much less
amplitude.