Here is some code for a nice "Honey Comb" mesh composed of equilateral triangles:
![]()
In[1]:=
![]()
![]()
Out[2]=

![]()
![[Graphics:HTMLFiles/index_6.gif]](HTMLFiles/index_6.gif)
![]()
In[3]:=
![]()
Out[3]=
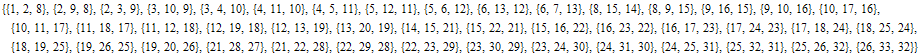
![]()
In[4]:=
![]()
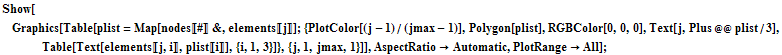
![[Graphics:HTMLFiles/index_13.gif]](HTMLFiles/index_13.gif)
![]()
In[6]:=
![]()
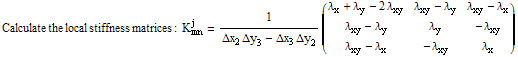
![]()
In[7]:=
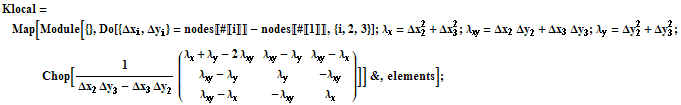
![]()
![]()
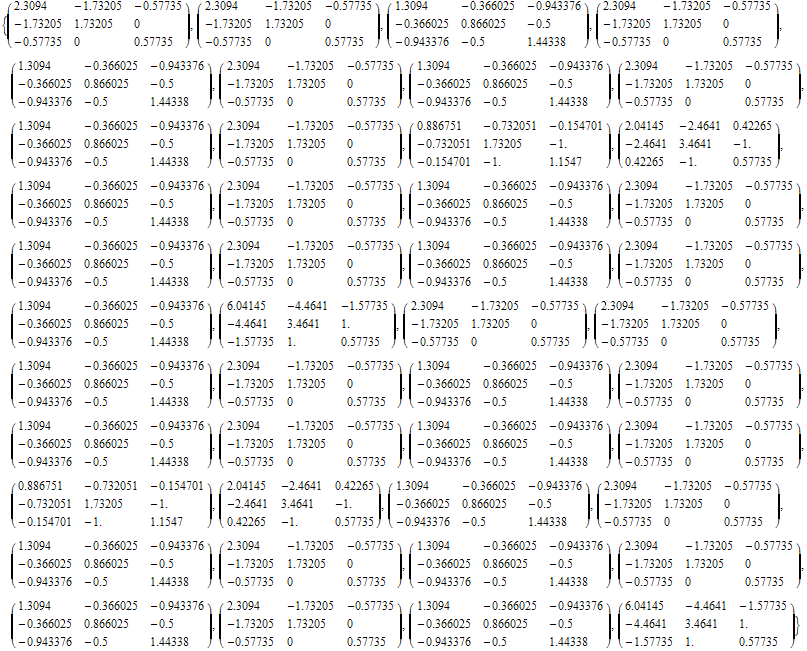
Out[8]=
![]()
In[9]:=
![]()
![]()
![]()
![]()
Out[11]//MatrixForm=

![]()
In[12]:=
![]()
![]()
In[13]:=
![]()
![]()
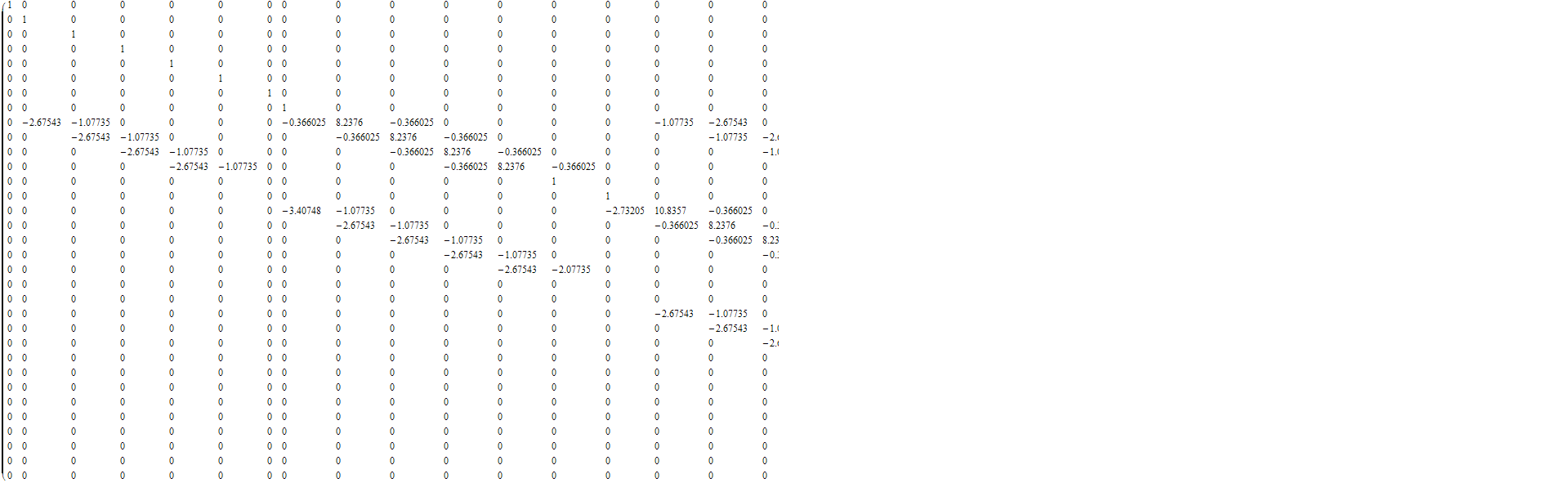
Out[14]//MatrixForm=
![]()
In[15]:=
![]()
Out[15]=
![]()
![]()
In[16]:=
![]()
![]()
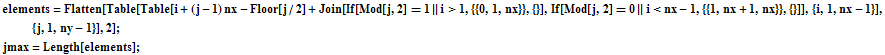
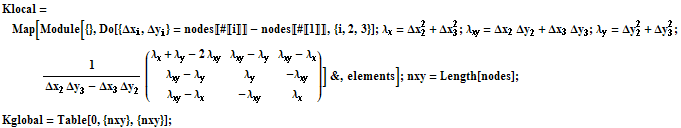
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/index_46.gif]](HTMLFiles/index_46.gif)
| Created by Mathematica (May 16, 2006) |