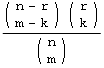
Table of distributions properties

by Nasser Abbasi, generated using Mathematica 6.0 .1

Table of discrete distributions functions, E (X), Var (X)

Name	X=	pmf P(X=K)	params	E(X)	Var(X)
Bernulli	Number of wins on this trial		p	p	(1-p) p
Binomial	Number of wins in n trials Each trial has p chance of winning		p,n	n p	n (1-p) p
Geometric	Number of trials needed to to obtain a success, Each trial has p chance of success		p
Negative Binomial	Number of trials needed to to obtain r successes, Each trial has p chance of success		r,p
Hypergeometric	Number of black balls drawn from urn when taking m balls without replacement. urn has total of n balls r black and m white		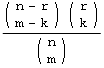m,r,n
Poisson	Number of events in given period		λ	λ	λ

Name	X=	pmf P(X=K)	params	E(X)	Var(X)
Bernulli	Number of wins on this trial		p	p	(1-p) p
Binomial	Number of wins in n trials Each trial has p chance of winning		p,n	n p	n (1-p) p
Geometric	Number of trials needed to to obtain a success, Each trial has p chance of success		p
Negative Binomial	Number of trials needed to to obtain r successes, Each trial has p chance of success		r,p
Hypergeometric	Number of black balls drawn from urn when taking m balls without replacement. urn has total of n balls r black and m white		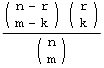m,r,n
Poisson	Number of events in given period		λ	λ	λ

Table of continuous distributions functions, E (X), Var (X)

Name	X=	pdf f(x)	params	E(X)	Var(X)
Normal		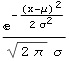	μ,σ	μ
Exponential			λ
Gamma			α,β	α β
ChiSquare		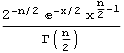	n	n	2 n
Chi		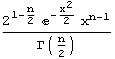	n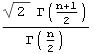
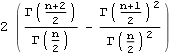Uniform			min,max
Cauchy		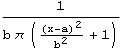	a,b	Indeterminate	Indeterminate
Beta			α,β
ExtremeValue		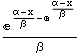	α,β	α+γ β
Gumbel		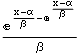	α,β	α-γ β
Laplace			μ,β	μ
HalfNormal			θ

Table of expected value of  functions of random variable

Name	Y, Function of random variable X	E(Y)
X=Normal	X	μ
X=Normal	2 X	2 μ
X=Normal
X=Normal
X=Normal
X=Poisson	2 X	2 λ
X=Poisson
X=Poisson
X=Poisson
X=Poisson
X=Poisson
X=Poisson			λ
X=Gamma(α,β)	2 X	2 α β
X=Gamma(α,β)
X=Gamma(α,β)
X=Gamma(α,β)
X=Gamma(α,β)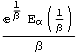
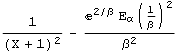X=Gamma(α,β)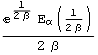
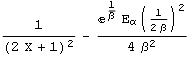X=Gamma(α,β)			α β
X=ChiSquare(n)	X	n	n (n+2)
X=ChiSquare(1)	X	1	3	2
X=ChiSquare(1)	2 X	2	12	8
X=ChiSquare(2)	X	2	8	4
X=ChiSquare(2)	2 X	4	32	16
X=T(n)	X
X=StudentTDistribution(1)	X	ExpectedValue[x,StudentTDistribution[1],x]
X=StudentTDistribution(1)	2 X	ExpectedValue[2 x,StudentTDistribution[1],x]
X=StudentTDistribution(2)	X	0
X=StudentTDistribution(2)	2 X	0

Some formulas

Var(X)=Cov(X,X)
	Cov(X,Y)=E(XY)-E(X)E(Y)	Cov(a+X,Y)=Cov(X,Y)
Cov(aX,bY)=ab Cov(X,Y)	Cov(X,Y+Z)=Cov(X,Y)+Cov(X,Z)
		E(X+Y)=E(X)+E(Y)
	M'(t=0)=E(X)
	Theorem B, page 138: Var(Y)=Var(E(Y|X))+E(Var(Y|X))

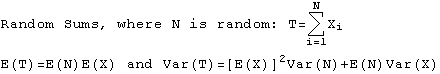Table of moment generating functions

Distribution		M'(t=0)=E(x)
Binomial		n p
Geometric
NegativeBinomial
Hypergeometric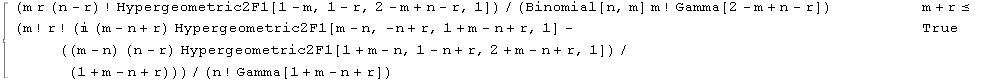
Poisson		λ
Normal		μ
Exponential
Gamma		α β
ChiSquare		n
Chi		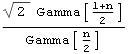	-n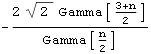
Uniform
Cauchy		a-b
Beta	Hypergeometric1F1[α,α+β,t]
ExtremeValue		α+EulerGamma β
Gumbel		α-EulerGamma β
Laplace		μ
HalfNormal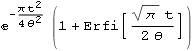

Created by Wolfram Mathematica 6.0 for Students - Personal Use Only  (02 February 2008)