This is an informal test comparing speed of Matlab, Mathematica and Maple on one common computational problem which is finding the rank of a square matrix.
For each \(N \times N\) matrix, \(5\) tests were run and the average value used. During running each test, the PC was not used as not to affect the test and no other programs were running. The PC used has 16 GB RAM, running 64 bit Windows 7 home premium OS.
The time given is in seconds.
|
matrix size (N) |
Maple 2016.1 (64 bit) |
Mathematica 11 (64 bit) |
Matlab 2016a (64 bit) |
| 500 |
0.036 |
0.024 |
0.0414 |
| 1000 |
0.141 |
0.134 |
0.138 |
| 1500 |
0.650 |
0.616 |
0.634 |
| 2000 |
2.08 |
2.033 |
2.053 |
| 2500 |
4.548 |
4.504 |
4.549 |
| 3000 |
2.313 | 8.393 | 2.595 |
| 3500 | 3.523 | 13.865 | 3.465 |
| 4000 | 5.215 | 22.088 | 5.052 |
| 4500 |
7.108 |
30.846 |
6.89 |
| 5000 |
8.129 |
43.079 |
8.005 |
| 5500 |
10.375 |
58.216 |
10.181 |
| 6000 |
13.543 |
75.655 |
13.466 |
| 6500 |
15.884 |
96.048 |
15.915 |
| 7000 |
19.673 |
120.505 |
19.000 |
| 7500 |
23.141 |
148.593 |
22.529 |
| 8000 |
28.789 |
180.311 |
28.095 |
Mathematica 11 score in this test went down from earlier test, while Maple and Matlab score went up. This issue seems to be due to the intel MKL version that the software is linked to.
More information on this can be found here cpu-timing-for-matrix-rank-calculation-difference-between-10-3-and-10-4-and-11-0
This test was run again for the new release of Mathematica 10.1 and a minor update for Maple 2015 to 2015.1. No changes were made to Matlab version or to the PC used from the last test and hence the Matlab test results were carried over from the last test.
Hardware used for this test is exactly the same as last time, and no changes made in the tests themselves.
The time given is in seconds. This is the time to find the rank for different matrix sizes (lower time is better). The results are in table 2 below.
|
matrix size (N) |
Maple 2015.1 (64 bit) |
Mathematica 10.1 (64 bit) |
Matlab 2015a (64 bit) |
| 500 |
0.046 |
0.03 |
0.04 |
| 1000 |
0.18 |
0.14 |
0.18 |
| 1500 |
0.71 |
0.65 |
0.66 |
| 2000 |
2.16 |
2.15 |
2.01 |
| 2500 |
4.8 |
4.66 |
4.61 |
| 3000 |
8.85 |
2.25(*) |
8.6 |
| 3500 | 14.48 | 3.42 | 14.05 |
| 4000 |
22.08 |
4.98 |
21.5 |
| 4500 |
32.18 |
6.97 |
31.1 |
| 5000 |
45.29 |
7.80 |
43.3 |
| 5500 |
60.3 |
9.66 |
58.4 |
| 6000 |
77.6 |
12.81 |
76.9 |
| 6500 |
100.1 |
14.70 |
97.5 |
| 7000 |
123.7 |
17.82 |
122.1 |
| 7500 |
153.9 |
22.49 |
151.9 |
| 8000 |
184.2 |
27.03 |
182.9 |
Mathematica 10.1 was surprisingly much faster on this test than 10.0.2. It seems Mathematica 10.1 is using different algorithm to compute the rank now to account for this drastic difference in speed improvement.
The speed boost was observed to occur at certain matrix size. At matrix size of 2500 or less, the same speed was obtained as with version 10.0.2. At matrix size over 2500, even by just one, a dramatic speed increase was seen. For \(n=2500\) Mathematica CPU was around 4.6 seconds which is the same as in 10.0.2, but by increasing the matrix size to \(n=2501\), CPU time went down to about 1.4 seconds. This is 3 times as fast for essentially the same matrix size. This result was reproducible. This seems to indicate that Mathematica internally uses the same algorithm as previous version for smaller size matrices, and then switches to different algorithm for larger matrices.
There was no noticeable change in Maple’s speed in this test between 2015 and Maple 2015.1.
Updated the test for the now released Maple 2015 (which would have been Maple 19) but the naming changed. Also updated for Matlab 2015a (64 bit) released on March 5, 2015.
Hardware used for this test is exactly the same as earlier test on July 2014, which is

The time given is in seconds. This is the time to find the rank for different matrix sizes (lower time is better). The results are in table 3 below.
|
matrix size (N) |
Maple 2015 (64 bit) |
Mathematica 10.02 (64 bit) |
Matlab 2015a (64 bit) |
| 500 |
0.043 |
0.047 |
0.04 |
| 1000 |
0.175 |
0.157 |
0.18 |
| 1500 |
0.64 |
0.67 |
0.66 |
| 2000 |
2.1 |
2.11 |
2.01 |
| 2500 |
4.8 |
4.67 |
4.61 |
| 3000 |
8.7 | 8.79 | 8.6 |
| 3500 | 14.5 | 14.15 | 14.05 |
| 4000 | 22.2 | 21.67 | 21.5 |
| 4500 |
31.7 |
31.42 |
31.1 |
| 5000 |
43.6 |
43.07 |
43.3 |
| 5500 |
57.9 |
58.8 |
58.4 |
| 6000 |
76.3 |
77.24 |
76.9 |
| 6500 |
96.7 |
98.21 |
97.5 |
| 7000 |
121.8 |
122.1 |
122.1 |
| 7500 |
151.2 |
151.81 |
151.9 |
| 8000 |
182.3 |
183.1 |
182.9 |
Finally, Maple now runs as fast as Mathematica and Matlab on this test. All three systems now have identical speed performance on this numerical test.
This indicates Maple 2015 is now using and linked to the same version of Intel optimized numerical libraries used by Matlab and Mathematica. On windows this will be intel math kernel library
The source code for the test is in the section below. No changes were made to the tests from last time.
Hardware used for this test

The time given is in seconds. This is the time to find the rank for different matrix sizes (lower time is better). The results are in table 4 below.
|
matrix size (N) |
Maple 18.01, 64 bit |
Mathematica 10, 64 bit |
Matlab 2013a, 32 bit |
| 500 |
0.07 |
0.031 |
0.043 |
| 1000 |
0.350 |
0.163 |
0.16 |
| 1500 |
1.46 |
0.72 |
0.63 |
| 2000 |
3.75 |
2.13 |
2.0 |
| 2500 |
7.47 |
4.72 |
4.5 |
| 3000 |
12.75 | 8.65 | 8.4 |
| 3500 | 19.85 | 14.22 | 14 |
| 4000 | 28.5 | 22.3 | 21.2 |
| 4500 |
40.5 |
31.23 |
30.8 |
| 5000 |
56.4 |
43.4 |
43 |
| 5500 |
73.65 |
58.14 |
58 |
| 6000 |
95.85 |
77.11 |
76 |
| 6500 |
124.84 |
97.61 |
96.5 |
| 7000 |
153.51 |
120.96 |
121.5 |
| 7500 |
199.4 |
149.58 |
150 |
| 8000 |
240.59 |
181.39 |
183 |
Matlab and Mathematica results are almost identical. This is most likely due to the fact that they both are linked to optimized versions of same numerical libraries. On windows this will be intel math kernel library
Maple 18.01 result is similar to its results in version 17 below. It seems to improve as the matrix size became larger, but its overall timing was still about \(25\%\) slower than timing of Matlab and Mathematica. It appears that Maple does not use intel-mkl or uses different version or the extra CPU time used comes from other operations done internally. Hard to say.
Matlab results are the same as those from the test below and used as is, since the same Matlab version and same PC and same amount of RAM was used in this test as the one below done on March 26, 2013. Only Maple and Mathematica versions has changed since then.
Description of the timing functions used is as follows
Command time[real](x) was used. Returns the real time used to evaluate
expression x.
Command AbsoluteTiming was used. Evaluates expr, returning a list of the
absolute number of seconds in real time that have elapsed.
Functions tic and toc were used. Work together to measure elapsed time.
(*kernel is restarted before each test as well*) Remove["Global`*"]; $HistoryLength = 0; Share[]; n = 7000; m = RandomReal[{}, {n, n}]; AbsoluteTiming[MatrixRank[m];]
restart; kernelopts(gcfreq= 2^22): UseHardwareFloats:= true: gc(): n:=7000: M:= LinearAlgebra:-RandomMatrix( n ,n ,generator=0.0 .. 1 ,outputoptions=[datatype=float[8]] ): time[real](LinearAlgebra:-LA_Main:-Rank(M));
clear all; n=2500; A=rand(n,n); tic(); rank(A); toc()
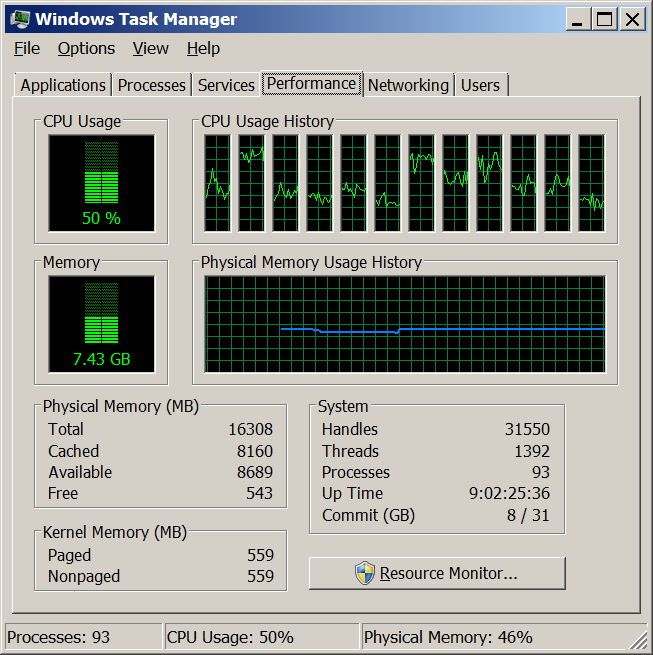
This is a screen shot showing typical memory and CPU usage during running of these tests on my PC
Hardware used is the same as above and timing functions are the same as above. The time given is in seconds. This is the time to find the rank for different matrix sizes (lower time is better). The results are in table 5 below.
|
matrix size (N) |
Maple 17, 64 bit |
Mathematica 9.01, 64 bit |
Matlab 2013a, 32 bit |
| 500 |
0.07 |
0.0312 |
0.043 |
| 1000 |
0.38 |
0.17 |
0.16 |
| 1500 |
1.5 |
0.65 |
0.63 |
| 2000 |
3.8 |
2.16 |
2.0 |
| 2500 |
7.8 |
4.68 |
4.5 |
| 3000 |
13 | 8.67 | 8.4 |
| 3500 | 20.9 | 14.1 | 14 |
| 4000 | 29 | 21.2 | 21.2 |
| 4500 |
42 |
30.9 |
30.8 |
| 5000 |
58 |
43.4 |
43 |
| 5500 |
75 |
58 |
58 |
| 6000 |
98 |
76 |
76 |
| 6500 |
124 |
96 |
96.5 |
| 7000 |
152 |
122 |
121.5 |
| 7500 |
198 |
150 |
150 |
| 8000 |
237 |
183 |
183 |
Matlab and Mathematica results are identical. This is most likely due to the fact that they both are linked to optimized versions of same numerical libraries. On windows this will be intel math kernel library
Maple result seems to improve as the matrix size became larger, but its overall timing was still about \(25\%\) slower than timing of Matlab and Mathematica.
This test is now old and not valid any more since new version of software exist. This is kept here for archiving only.
Hardware used for this test
In the table below, the first column is \(N\), the matrix size. All values in the matrix are in seconds.
+--------------+---------------+----------------+ | Maple | Mathematica | Matlab | |----+----+----+----+-----+----+-----+----+-----+ |Rand|Rank|tot |Rand|Rank |tot |Rand |Rank|tot | +----+--------------+----+-----+----+-----+----+-----+ |500 |.031|.545|.56 |0.04|0.55 |0.56|0.04 |0.9 |0.94 | +----+----+----+----+----+-----+----+-----+----+-----+ |1000|0.11|3.74|3.84|.2 |3.8 | 4 |.11 |5.7 |5.8 | +----+----+----+----+----+-----+----+-----+----+-----+ |1500|0.25|11.7|11.9|.4 |12.3 |12.7|.14 |22 |22.15| +----+----+----+----+----+-----+----+-----+----+-----+ |2000|0.42|29.8|30.2|.75 |30 |31 |.26 |44 |44.3 | +----+----+----+----+---------------+-----+----+-----+ |2500|0.67|50.6|51.2|1.2 |55 |56 |.34 |96 |96.3 | +----+----+----+----+----+-----+----+-----+----+-----+ |3000|0.98|94 |95 |1.8 |85 |87 |.47 |142 | 143 | +----+----+----+----+----+-----+----+-----+----+-----+ |3500|1.3 |167 |170 |2.3 |132 |135 |.61 |262 | 263 | +----+----+----+----+----+-----+----+-----+----+-----+ |4000|1.75|* | |3.27|236 |240 |.83 |340 | 341 | +----+----+----+----+----+-----+----+-----+----+-----+ |4500|2.15|* | |3.98|304 |308 |.93 |545 | 546 | +----+----+----+----+----+-----+----+-----+----+-----+ |5000|2.67|* | |4.7 |425 |430 |1.46 |671 | 672 | +----+----+----+----+----+-----+----+-----+----+-----+ (*): Maple gave this error: Error, (in Matrix) not enough memory to allocate rtable
For generation of random matrix, Maple was close second to Matlab for smaller Matrix sizes, then Matab pulled ahead as the matrix size increased.
But overall for all 3 systems, this part took insignificant amount of time compared to rank calculation. So this part did not affect the overall performance.
For Rank calculation, Maple and Mathematica performance was very close to each others for small size matrices. Almost identical performance. This was up to matrix of size 2500.
Mathematica performance then became a little better compared to Maple’s. At Matrix size \(4000 \times 4000\) Maple test was terminated due to a failed memory error problem. The amount of RAM needed is \((4000)(4000)(8)(4)= 512\) MB.
This error should not therefore occur. It seems to be an internal problem in Maple since both Matlab and Mathematica are able to handle up to \(5000 \times 5000\) matrices.
Mathematica was almost \(60\%\) faster than Matlab for \(5000 \times 5000\) matrix rank calculation. This is a very good result for Mathematica.
Matlab was the fastest in all the tests for the Random matrix generation.
restart; kernelopts(gcfreq= 2^22): UseHardwareFloats:= true: gc(): n:=3500: t0:= time(): M:= LinearAlgebra:-RandomMatrix( n ,n ,generator=0.0 .. 1 ,outputoptions=[datatype=float[8]] ): #gc(): randTime:= time()-t0; LinearAlgebra:-LA_Main:-Rank(M): rankTime:= time()-(t0+randTime); total:=rankTime+randTime;
Remove["Global`*"]; Share[]; n = 4000; Timing[m = Table[Random[], {i, 1, n}, {j, 1, n}]; ] Timing[MatrixRank[m]]
n=5000; t=cputime; A=rand(n,n); cputime-t t=cputime; rank(A); cputime-t