HW 4.16
Nasser Abbasi
Problem: write a program than uses Netwton’s method to find the roots of functions. Test your program on the following cases
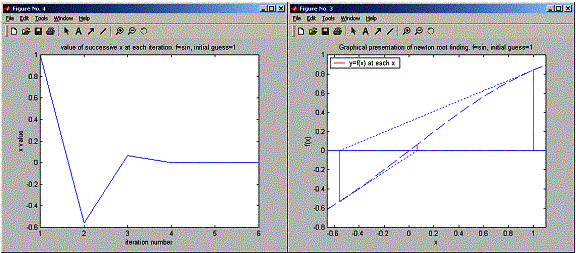
(a) f(x)=sin(x); x1=1
(b) f(x)=sin(X); x1=2
(c) f(x)=x^10; x1=1
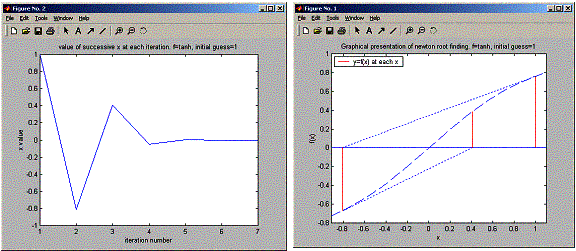
(d) f(x)=tanh(x); x1=1
(e) f(x)=tanh(x); x1=3
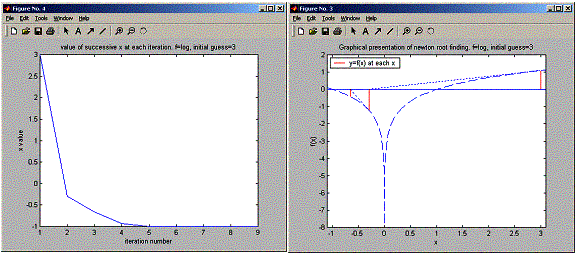
(f) f(x)=ln(x); x1=3
solution
output
» nma_HW_4_16
program to solve problem 4.16 using newton method
to find roots of some equations
Nasser Abbasi, San Jose State Univ. Phys 240.
enter problem number to solve [a,b,c,d,e,f]:'a'
enter min difference between successive x values to halt root finding:0
iteration number 1, current x=1, sin(1)=0.841471
iteration number 2, current x=-0.557408, sin(-0.557408)=-0.528988
iteration number 3, current x=0.0659365, sin(0.0659365)=0.0658887
iteration number 4, current x=-9.57219e-005, sin(-9.57219e-005)=-9.57219e-005
iteration number 5, current x=2.92357e-013, sin(2.92357e-013)=2.92357e-013
iteration number 6, current x=0, sin(0)=0
After 6 iterations, x=0, sin(x)=0
»
» nma_HW_4_16
» nma_HW_4_16
program to solve problem 4.16 using newton method
to find roots of some equations
Nasser Abbasi, San Jose State Univ. Phys 240.
enter problem number to solve [a,b,c,d,e,f]:'b'
enter min difference between successive x values to halt root finding:0
iteration number 1, current x=2, sin(2)=0.909297
iteration number 2, current x=4.18504, sin(4.18504)=-0.864144
iteration number 3, current x=2.46789, sin(2.46789)=0.623881
iteration number 4, current x=3.26619, sin(3.26619)=-0.124272
iteration number 5, current x=3.14094, sin(3.14094)=0.000648741
iteration number 6, current x=3.14159, sin(3.14159)=-9.10111e-011
iteration number 7, current x=3.14159, sin(3.14159)=1.22465e-016
iteration number 8, current x=3.14159, sin(3.14159)=1.22465e-016
After 8 iterations, x=3.14159, sin(x)=1.22465e-016
»

» nma_HW_4_16
» nma_HW_4_16
program to solve problem 4.16 using newton method
to find roots of some equations
Nasser Abbasi, San Jose State Univ. Phys 240.
enter problem number to solve [a,b,c,d,e,f]:'c'
enter min difference between successive x values to halt root finding:0.001
iteration number 1, current x=1, f_partc(1)=1
iteration number 2, current x=0.9, f_partc(0.9)=0.348678
iteration number 3, current x=0.81, f_partc(0.81)=0.121577
iteration number 4, current x=0.729, f_partc(0.729)=0.0423912
…. Rest removed….
teration number 45, current x=0.00969774, f_partc(0.00969774)=7.35706e-021
iteration number 46, current x=0.00872796, f_partc(0.00872796)=2.56525e-021
After 46 iterations, x=0.00872796, f_partc(x)=2.56525e-021
»

» nma_HW_4_16
» nma_HW_4_16
program to solve problem 4.16 using newton method
to find roots of some equations
Nasser Abbasi, San Jose State Univ. Phys 240.
enter problem number to solve [a,b,c,d,e,f]:'d'
enter min difference between successive x values to halt root finding:0
iteration number 1, current x=1, tanh(1)=0.761594
iteration number 2, current x=-0.81343, tanh(-0.81343)=-0.671478
iteration number 3, current x=0.409402, tanh(0.409402)=0.387965
iteration number 4, current x=-0.0473049, tanh(-0.0473049)=-0.0472697
iteration number 5, current x=7.06028e-005, tanh(7.06028e-005)=7.06028e-005
iteration number 6, current x=-2.34625e-013, tanh(-2.34625e-013)=-2.34625e-013
iteration number 7, current x=0, tanh(0)=0
After 7 iterations, x=0, tanh(x)=0
»
» nma_HW_4_16
program to solve problem 4.16 using newton method
to find roots of some equations
Nasser Abbasi, San Jose State Univ. Phys 240.
enter problem number to solve [a,b,c,d,e,f]:'e'
enter min difference between successive x values to halt root finding:0
iteration number 1, current x=3, tanh(3)=0.995055
iteration number 2, current x=-97.8566, tanh(-97.8566)=-1
halting search for root since slop is 0iteration number 2, current x=-97.8566, tanh(-97.8566)=-1
After 2 iterations, x=-97.8566, tanh(x)=-1
»

» nma_HW_4_16
program to solve problem 4.16 using newton method
to find roots of some equations
Nasser Abbasi, San Jose State Univ. Phys 240.
enter problem number to solve [a,b,c,d,e,f]:'f'
enter min difference between successive x values to halt root finding:0
iteration
number 1, current x=3, log(3)=1.09861
iteration
number 2, current x=-0.295837, log(-0.295837)=-1.21795
iteration
number 3, current x=-0.656151, log(-0.656151)=-0.421365
iteration
number 4, current x=-0.932629, log(-0.932629)=-0.0697473
iteration
number 5, current x=-0.997678, log(-0.997678)=-0.00232485
iteration
number 6, current x=-0.999997, log(-0.999997)=-2.69828e-006
iteration
number 7, current x=-1, log(-1)=-3.64031e-012
iteration
number 8, current x=-1, log(-1)=0
iteration
number 9, current x=-1, log(-1)=0
Warning:
Imaginary parts of complex X and/or Y arguments ignored.
>
In C:\MATLABR11\toolbox\matlab\specgraph\fplot.m at line 139
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
(reportResult) at line 133
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
(findRoot) at line 113
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
at line 54
Warning:
Imaginary parts of complex X and/or Y arguments ignored.
>
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
(reportResult) at line 144
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
(findRoot) at line 113
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
at line 54
Warning:
Imaginary parts of complex X and/or Y arguments ignored.
>
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
(reportResult) at line 142
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
(findRoot) at line 113
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
at line 54
Warning:
Imaginary parts of complex X and/or Y arguments ignored.
>
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
(reportResult) at line 144
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
(findRoot) at line 113
In
D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW11\nma_hw_4_16.m
at line 54
After
9 iterations, x=-1, log(x)=0
»
SOURCE CODE
function nma_HW_4_16()
%
program to solve problem 4.16 using newton method
% to
find roots of some equations
% Nasser
Abbasi, San Jose State Univ. Phys 240.
clear all; help
nma_hw_4_16;
part = input('enter problem number to solve [a,b,c,d,e,f]:');
tol = input('min
difference between successive x to halt root finding:');
% use
matrix P to keep track of the x,y coordinates as
% we get
close to the root, to plot at the end.
% P has
4 columns. at each guess we store into P the following:
% the
x,y coordinates of the guess point on the x-axis and the
% x,y
cooridnates of f(x).
switch part
case 'a'
% f(x)= sin(x), x1=1
f = 'sin';
df = 'cos';
initialGuess = 1;
findRoot(f,df,initialGuess,tol);
case 'b'
f = 'sin';
df = 'cos';
initialGuess = 2;
findRoot(f,df,initialGuess,tol);
case 'c'
f = 'f_partc';
df = 'df_partc';
initialGuess = 1;
findRoot(f,df,initialGuess,tol);
case 'd'
f = 'tanh';
df = 'df_partd';
initialGuess = 1;
findRoot(f,df,initialGuess,tol);
case 'e'
f='tanh';
df='df_partd';
initialGuess=3;
findRoot(f,df,initialGuess,tol);
case 'f'
f='log';
df='df_partf';
initialGuess=3;
findRoot(f,df,initialGuess,tol);
end
%%%%%%%%%%%%%%%%%%%%%%%
%function
findRoot(f,df,x1)
%
%%%%%%%%%%%%%%%%%%%%%%%%%
function findRoot(f,df,initialGuess,tol)
% set
some upper limit on number of interations
MAX_NUMBER_OF_ITERATIONS =
1000;
i = 1;
x(i) = initialGuess;
k = 1;
% x,y coordinates of the
initial guess
P(k,1)= x(i); P(k,2)=0;
P(k,3)=x(i); P(k,4)=feval(f,x(i));
y(i) =
feval(f,x(i));
diffy(i) = feval(df,x(i));
while( y(i) ~= 0 & i <
MAX_NUMBER_OF_ITERATIONS)
fprintf('iteration number
%d, current x=%g, %s(%g)=%g\n',...
i,x(i),f,x(i),feval(f,x(i)) );
%
% check is slop is zero. If so, stop
the search for the root.
%
if( diffy(i) == 0 )
fprintf('halting search
for root since slop is 0');
break;
end
i=i+1;
x(i) = x(i-1) - ( y(i-1) / diffy(i-1) );
x(i) = real(x(i));
% keep the real part, in case it becomes
complex.
y(i) =
feval(f,x(i));
diffy(i) = feval(df,x(i));
%
% stop looking for a root when successive x are within user
supplied
% tolerance
%
if( abs(x(i) - x(i-1))
<= tol )
break;
end
k = k+1;
P(k,1) = x(i); P(k,2)=0; P(k,3)= x(i-1); P(k,4)=
feval(f,x(i-1));
k = k+1;
P(k,1) = x(i); P(k,2)=0; P(k,3)= x(i); P(k,4)= feval(f,
x(i));
end
fprintf('iteration number %d,
current x=%g, %s(%g)=%g\n', ...
i,x(i),f,x(i),feval(f,x(i)) );
reportResult(f,P,x,y,tol);
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
function reportResult(f,p)
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%
function reportResult(f,P,x,y,tol)
figure;
k=1;
plot( [P(k,1) P(k,3)] , [P(k,2) P(k,4)],'r');
hold on;
[ROW,COL] = size(P);
xRange = [min(P(:,1))-0.1 max(P(:,1))+0.1];
if( isequal(f,'f_partc'))
plot(y,'--');
else
fplot(f,xRange,'--');
end
% draw xaxis line
plot( [xRange(1) xRange(2)], [0 0],'-');
% plot the first 4 iterations
for illustations
while( 1 )
k=k+1;
plot( [P(k,1) P(k,3)] , [P(k,2) P(k,4)],':');
k=k+1;
plot( [P(k,1) P(k,3)] , [P(k,2) P(k,4)],'r');
if( k == ROW | k > 4)
break;
end
end
title(sprintf('Graphical
presentation of newton root finding. f=%s, x1=%d',...
f,x(1)));
xlabel('x');
ylabel('f(x)');
legend('y=f(x) at each x',2);
%
% plot iteration number i vs
x_i
%
figure;
fprintf('After %d iterations,
x=%g, %s(x)=%g\n',...
length(x),x(end),f,feval(f,x(end)));
plot(x,'-');
set(gca,'XTick',[1:1:length(x)]);
title(sprintf('value of
successive x at each iteration. f=%s, x1=%d',…
f,x(1)));
xlabel('iteration number');
ylabel('x value');
return;
%%%%%%%%%%%%%%%%%%%%%
%
function f_partc()
%
%%%%%%%%%%%%%%%%%%%%%%
function f=f_partc(x)
f=x^10;
%%%%%%%%%%%%%%%%%%%%
%
function df_partc(x)
%
%%%%%%%%%%%%%%%%%%%%
function df=df_partc(x)
df=10*x^9;
%%%%%%%%%%%%%%%%%%%%%%%%%
%function
df=df_partd
%
%%%%%%%%%%%%%%%%%%%%%%%%%
function df=df_partd(x)
df=1-(tanh(x))^2;
%%%%%%%%%%%%%%%%%%%%%%%%%
%function
df=df_partf
%
%%%%%%%%%%%%%%%%%%%%%%%%%
function df=df_partf(x)
df=1/x;