Problem 6.8

Nasser Abbasi

OUTPUT

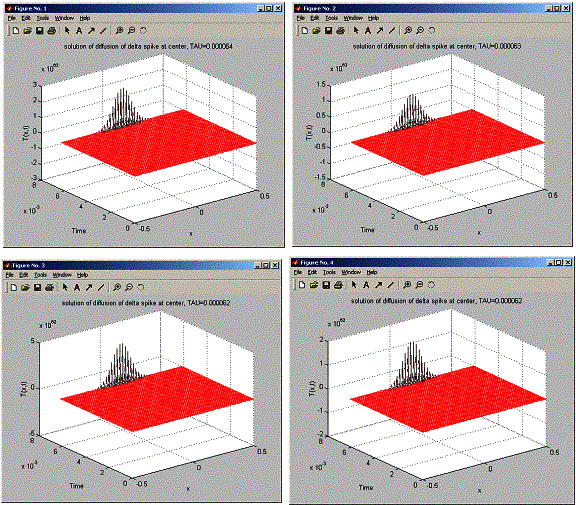
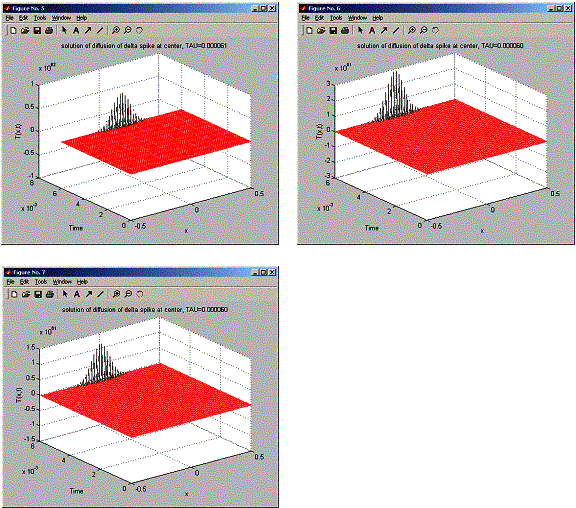
In this problem, need to find if Richardson scheme is not numerically stable for all tau.

To solve this, I find t_sigma, and then try for 6 values of tau starting from 3% below t_sigma up to 3% above t_sigma, each time at an increment of 1% of t_sigma.

The results shows that at the end of the run, T is always unstable for all selected tau.

» nma_problem_6_8

solves diffusion partial differential equation

for Dirchlet bounday conditions using Richardson

method. Problem 6.8

Nasser Abbasi

Enter number of space grid points:91

Enter number of time steps:100

t_sigma = 0.000062 seconds

Trying to see if stable of not for TAU=0.000064 seconds

Trying to see if stable of not for TAU=0.000063 seconds

Trying to see if stable of not for TAU=0.000062 seconds

Trying to see if stable of not for TAU=0.000062 seconds

Trying to see if stable of not for TAU=0.000061 seconds

Trying to see if stable of not for TAU=0.000060 seconds

Trying to see if stable of not for TAU=0.000060 seconds

»

CODE

function nma_problem_6_8()

%

% solves diffusion partial differential equation

% for Dirchlet bounday conditions using Richardson

% method. Problem 6.8

% Nasser Abbasi

help nma_problem_6_8; clear all; close all;

N = input('Enter number of space grid points:');

numberOfTimeSteps = input('Enter number of time steps:');

k = 1;

L = 1; % space distance total from -L/2 to L/2

x0 = 0; % where we want to find the solution at.

h = L/(N-1); % space distance between each point.

%

% Find t_sigma, and try number of Tau's below and above t_sigma

% to see if unstable for all of the Tau. use 1% of t_sigma as step size

% for tau variation around t_sigma.

t_sigma = h^2/(2*k);

t_sigma_factor = t_sigma * (1/100);

fprintf('t_sigma = %1.6f seconds\n',t_sigma);

for(m = -3:3)

currentTau = t_sigma-(m*t_sigma_factor);

coeff = 2 * k * currentTau /h^2;

fprintf('Trying to see if stable of not for TAU=%1.6f seconds\n',currentTau);

%

% reserve space for the whole T(x,t) solution matrix

%

T = zeros(numberOfTimeSteps, N);

T(1,round(N/2)) = 1/h; % initial condition for delta at center

%

% set the Nuemman bounday conditions before

% each time step calculation of T

%

T(:,1) = 0;

T(:,N) = 0;

%

% Make the first step in time using FTCS, notice using 1/2

% coef since FTCS does not have the '2' factor as in

% Richardson

%

for( i = 2:N-1 )

T(2,i) = T(1,i) + (1/2) * coeff * ( T(1,i+1) + T(1,i-1) - 2*T(1,i));

end

%

% Make the rest of time steps using Richardson

%

for( n = 2: numberOfTimeSteps - 1)

for( i = 2:N-1 )

T(n+1,i) = T(n-1,i) + coeff*( T(n,i+1) + T(n,i-1) - 2*T(n,i));

end

end

%

% Now do the plots.

%

spaceVector = (0:N-1)*h - L/2;

timeVector = (0:numberOfTimeSteps-1) * currentTau;

figure;

colormap([0 0 0;1 0 0]);

mesh( spaceVector, timeVector, T );

title(sprintf('solution of diffusion of delta spike at center, TAU=%1.6f',currentTau));

xlabel('x');

ylabel('Time');

zlabel('T(x,t)');

end % for try