7.2

Nasser Abbasi

OUTPUT

I first show the output for the three methods, for tau=0.015, 0.02 and 0.03, all for frequency 10*pi.

Conclusion for frequency 10*pi :

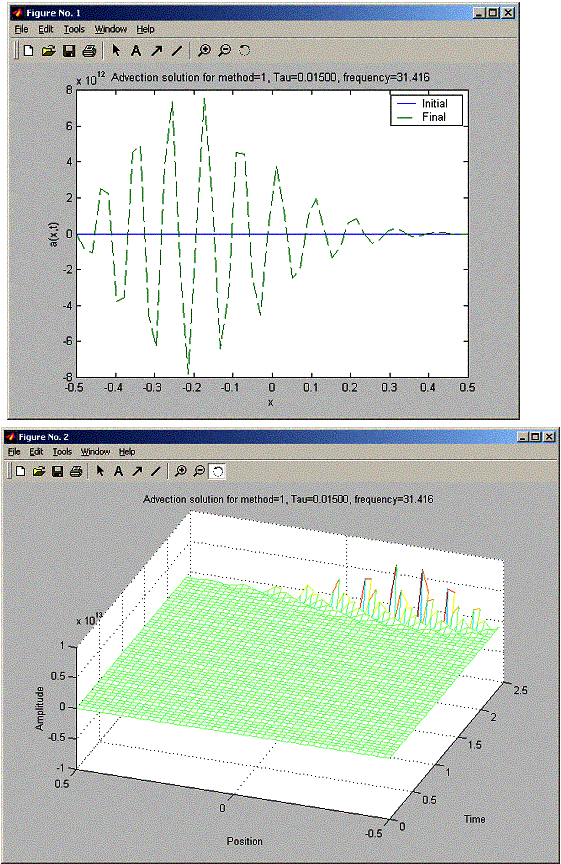
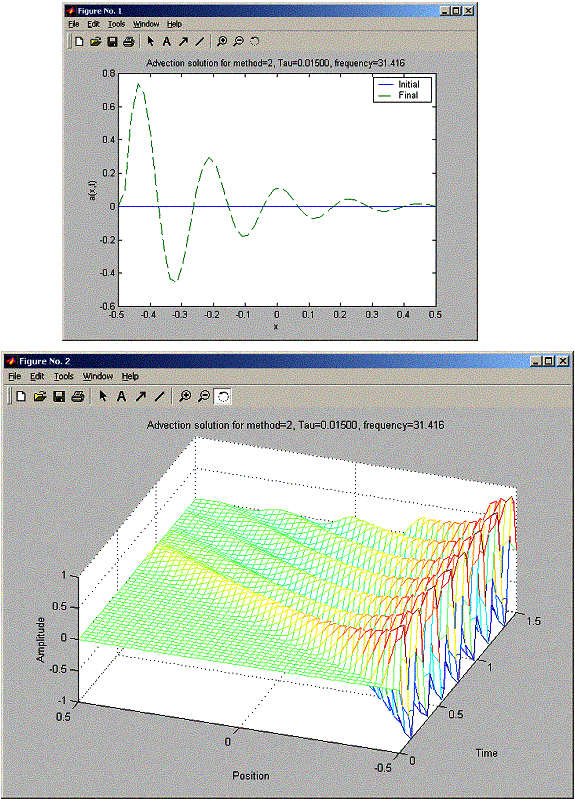
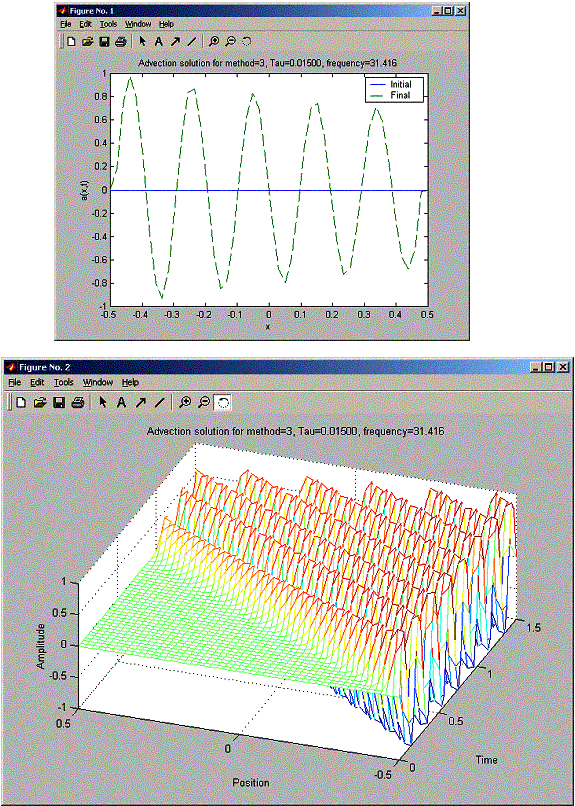
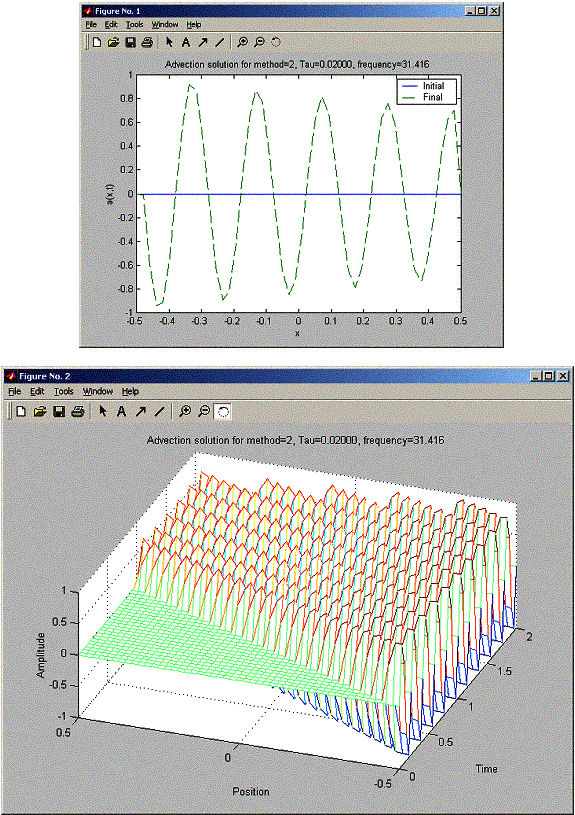
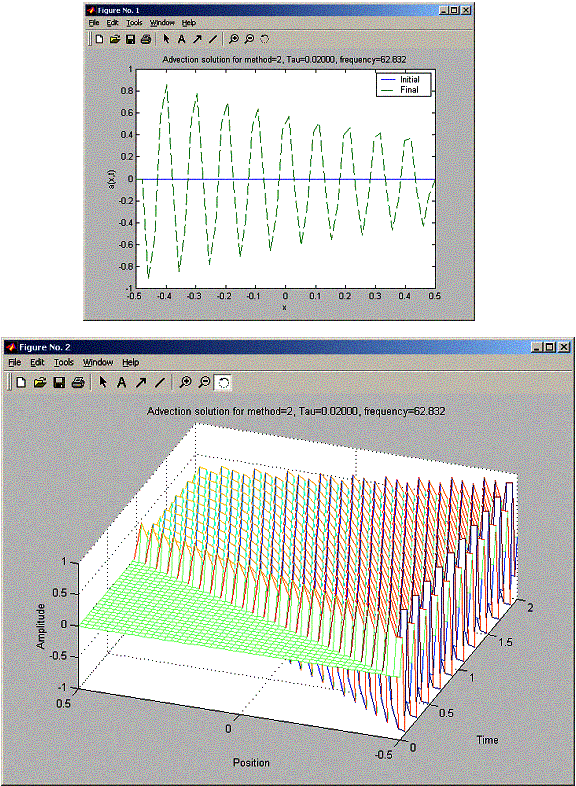
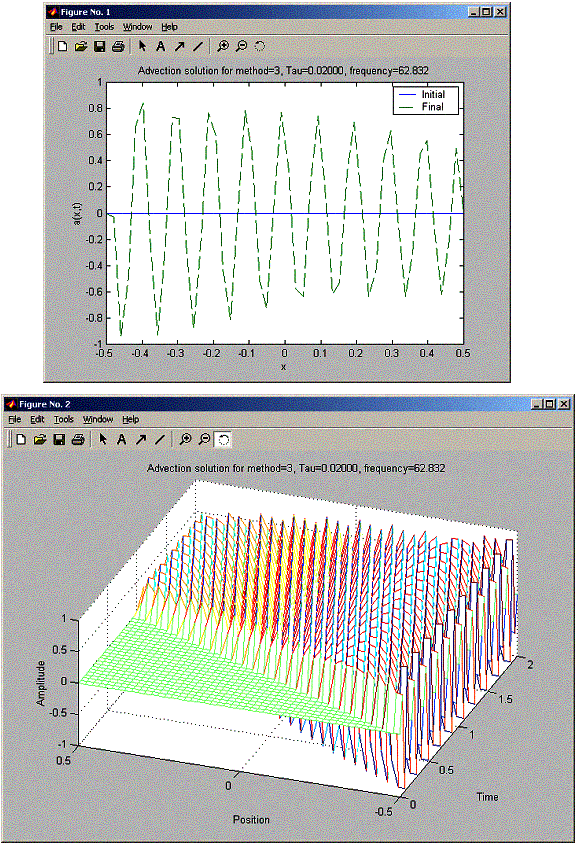
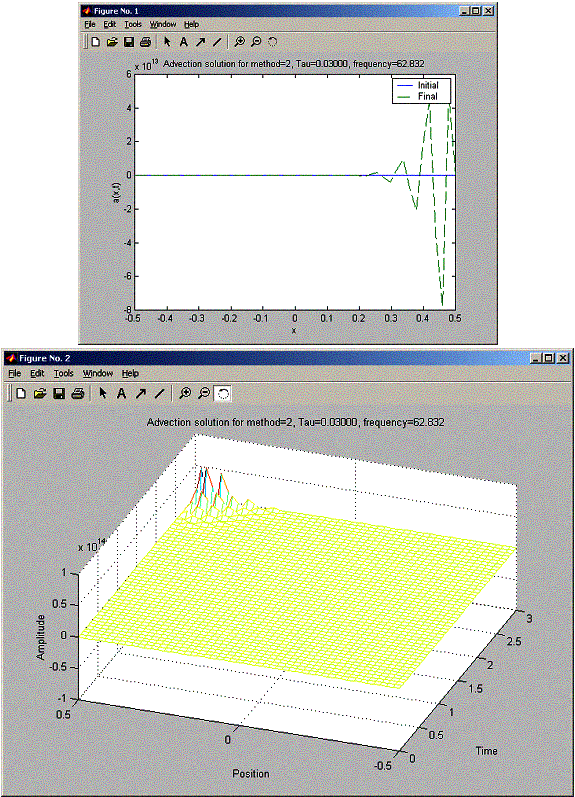
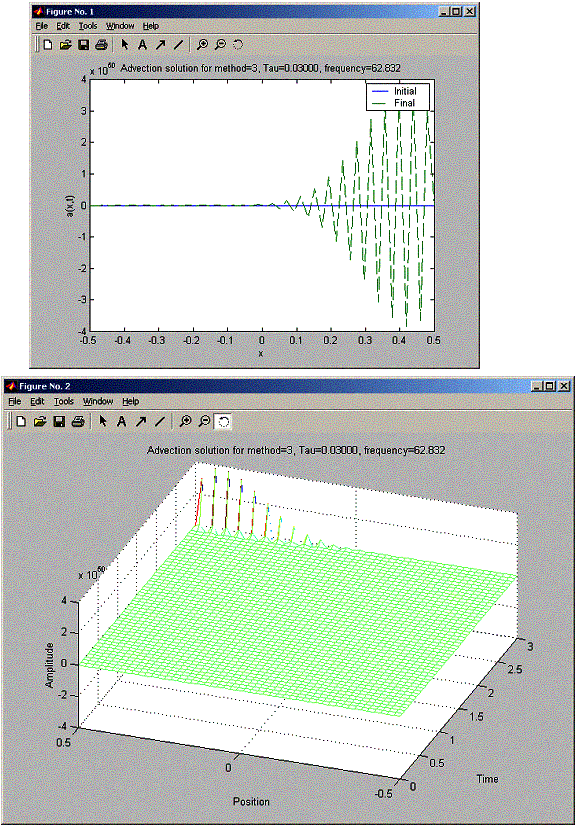
h = 0.0204 for all these problems. So h/c = 0.0204 seconds. When trying for tau for 0.015, 0.02, and 0.03, FTCS was unstable for all tau, and the stability becames worst as tau increased (amplitude at final was much larger as tau increased). For the Lax method, when tau was less than 0.02, there was a damping in the final sin amplitude as x increased from –L/2 to L/2. While the Lax-Wendroff did not suffer from this damping. At Tau 0.02, Lax and Lax-Wendroff looked the same. At tau = 0.03 Lax-Wendroff became unstable earlier than Lax. The final plot shows Lax-Wendroff starting to blow up at x= 0.1L, while Lax managed to hold well until x=0.3L, but still at X=L/2, Lax had much smaller blow up signal amplitude than Lax-Wendroff.

When doubling the frequency of the sin signal. At tau below 0.02, Lax damps more than at the lower freuqncy (lower amplitude at final for tau=20pi compared to 10pi frequency),

Also Lax-Wendroff at double the frequency damps more. At tau=0.03,

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :1

You selected method 1

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.015

Enter number of steps: 160

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :2

You selected method 2

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.015

Enter number of steps: 100

»

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.015

Enter number of steps: 100

»

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :1

You selected method 1

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.02

Enter number of steps: 150

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :2

You selected method 2

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.02

Enter number of steps: 100

»

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.02

Enter number of steps: 100

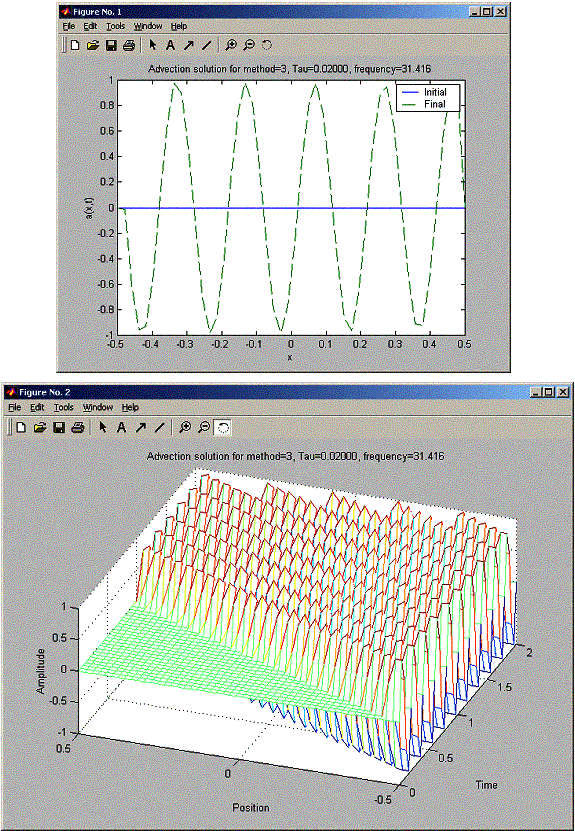
» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :1

You selected method 1

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.03

Enter number of steps: 150

»

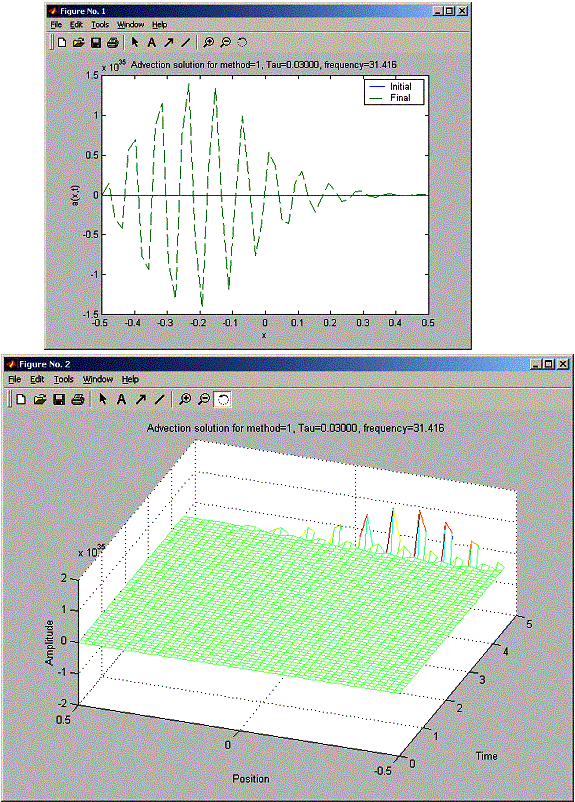
» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :2

You selected method 2

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.03

Enter number of steps: 100

»

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:10*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.03

Enter number of steps: 100

»

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :2

You selected method 2

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:20*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.015

Enter number of steps: 100

»

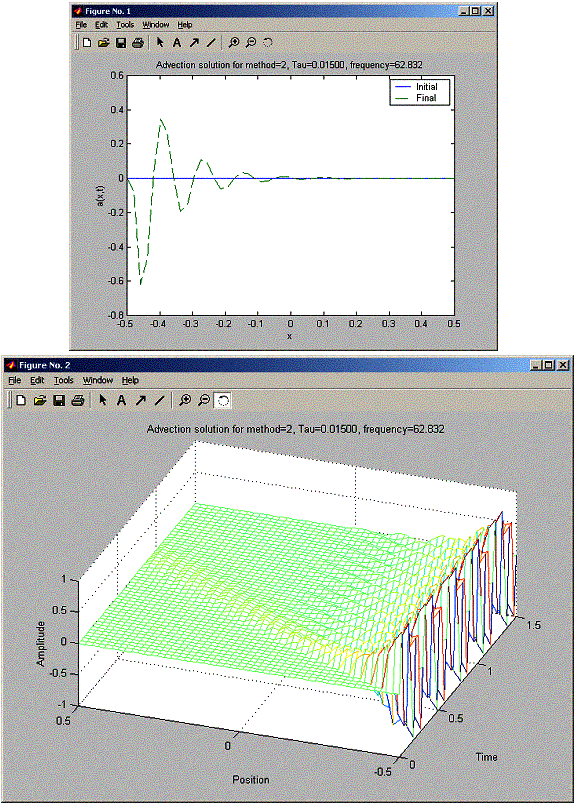
» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:20*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.015

Enter number of steps: 100

»

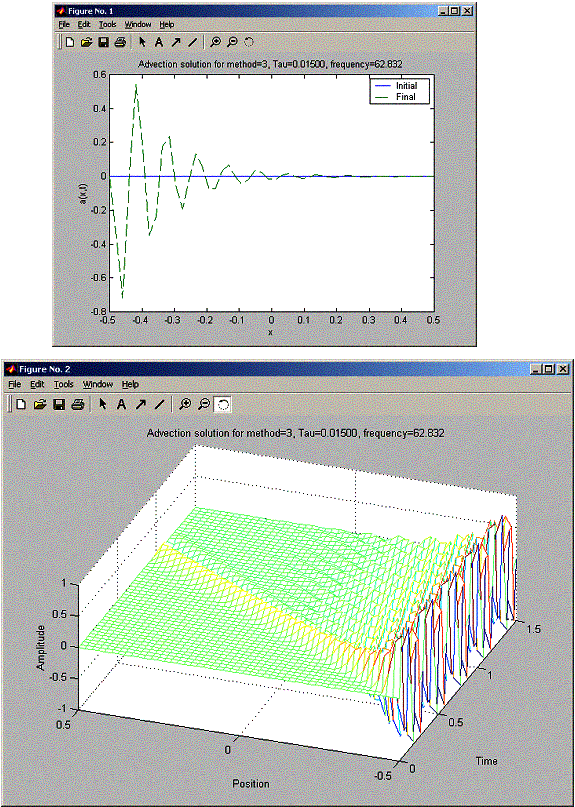
» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :2

You selected method 2

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:20*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.02

Enter number of steps: 100

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:20*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.02

Enter number of steps: 100

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :2

You selected method 2

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:20*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.03

Enter number of steps: 100

» nma_advect_problem_7_2

nma_advect_problem_7_2 - Program to solve the

advection equation using the various hyperbolic PDE schemes

solves problem 7.2 in book

Nasser Abbasi

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter number of grid points: 50

Enter the frequncy w of the sin signal at the bounday:20*pi

Time for wave to move one grid spacing is 0.0204082

Enter time step: 0.03

Enter number of steps: 100

»

CODE:

function nma_advect_problem_7_2()

% nma_advect_problem_7_2 - Program to solve the

% advection equation using the various hyperbolic PDE schemes

% solves problem 7.2 in book

% Nasser Abbasi

clear all; help nma_advect_problem_7_2; % Clear memory and print header

%* Select numerical parameters (time step, grid spacing, etc.).

try_again=1;

while(try_again)

method = input('select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :');

if( method<1 | method>3 )

fprintf('Please try again, choice must be 1 or 2 or 3.\n');

else

try_again=0;

fprintf('You selected method %d\n',method);

end

end

N = input('Enter number of grid points: ');

L = 1.; % System size

%h = L/N; % Grid spacing FOR PERIODIC B.C.

h = L/(N-1); % Grid spacing for Dirichlet B.C.

c = 1; % Wave speed

omega = input('Enter the frequncy w of the sin signal at the bounday:');

fprintf('Time for wave to move one grid spacing is %g\n',h/c);

tau = input('Enter time step: ');

coeff = -c*tau/(2.*h); % Coefficient used by all schemes

coefflw = 2*coeff^2; % Coefficient used by L-W scheme

%fprintf('Wave circles system in %g steps\n',L/(c*tau));

nStep = input('Enter number of steps: ');

%* Set Initial conditions.

sigma = 0.1; % Width of the Gaussian pulse

k_wave = pi/sigma; % Wave number of the cosine

%x = ((1:N)-1/2)*h - L/2; % Coordinates of grid points for periodic.

x = ((1:N)-1)*h - L/2; % Coordinates of grid points for Dirichlet

% set Initial conditions as a Gaussian-cosine pulse

%a = cos(k_wave*x) .* exp(-x.^2/(2*sigma^2));

a=zeros(N,1);

% Use periodic boundary conditions

%ip(1:(N-1)) = 2:N;

%ip(N) = 1; % ip = i+1 with periodic b.c.

%im(2:N) = 1:(N-1);

%im(1) = N; % im = i-1 with periodic b.c.

%use Dirichlet

ip(1:N-2) = 3:N;

im(1:N-2) = 1:N-2;

%* Initialize plotting variables.

iplot = 1; % Plot counter

aplot(:,1) = a(:); % Record the initial state

tplot(1) = 0; % Record the initial time (t=0)

nplots = 50; % Desired number of plots

plotStep = nStep/nplots; % Number of steps between plots

%* Loop over desired number of steps.

for iStep=1:nStep %% MAIN LOOP %%

%* Compute new values of wave amplitude using FTCS,

% Lax or Lax-Wendroff method.

if( method == 1 ) %%% FTCS method %%%

a(1) = sin(omega*(iStep)*tau);

a(N) = 0;

a(2:N-1) = a(2:N-1) + coeff*(a(ip)-a(im));

else

if( method == 2 ) %%% Lax method %%%

a(1) = sin(omega*(iStep)*tau);

a(N) = 0;

a(2:N-1) = .5*(a(ip)+a(im)) + coeff*(a(ip)-a(im));

else %%% Lax-Wendroff method %%%

a(1) = sin(omega*(iStep)*tau);

a(N) = 0;

a(2:N-1) = a(2:N-1) + coeff*(a(ip)-a(im)) + ...

coefflw*(a(ip)+a(im)-2*a(2:N-1));

end

end

%* Periodically record a(t) for plotting.

if( rem(iStep,plotStep) < 1 ) % Every plot_iter steps record

iplot = iplot+1;

aplot(:,iplot) = a(:); % Record a(i) for ploting

tplot(iplot) = tau*iStep;

%fprintf('%g out of %g steps completed\n',iStep,nStep);

end

end

%* Plot the initial and final states.

figure(1);

clf; % Clear figure 1 window and bring forward

plot(x,aplot(:,1),'-',x,a,'--');

legend('Initial ','Final');

xlabel('x');

ylabel('a(x,t)');

title(sprintf('Advection solution for method=%d, Tau=%1.5f, frequency=%3.3f',method,tau,omega));

pause(1); % Pause 1 second between plots

%* Plot the wave amplitude versus position and time

figure(2); clf; % Clear figure 2 window and bring forward

mesh(tplot,x,aplot);

ylabel('Position'); xlabel('Time'); zlabel('Amplitude');

view([-70 50]); % Better view from this angle

title(sprintf('Advection solution for method=%d, Tau=%1.5f, frequency=%3.3f',method,tau,omega));