Problem 7.12

Nasser Abbasi

Output:

Part (a)

For light traffic, the peak of the density moves forward at a speed of 9.3 meters/second.

The modified program determines the direction of the density wave and the speed. This is an example run for rho_zero = ¼ rho_max (ran it 3 times, once for each method)

RUN 1

» nma_problem_7_12

traffic - Program to solve the generalized Burger

equation for the traffic at a stop light problem

solves problem 7.12

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :1

You selected method 1

Enter the number of grid points: (suggest 80):80

Enter value for L, sytem size in meters. (suggest 400) :400

Suggested timestep is 0.2

Enter time step (tau): 0.02

Last car starts moving after 200 steps

Enter number of steps: 200

Maximum density (rho max) suggest 1 :1

Enter value for alpha (suggested 1/5):1/5

Enter value for sigma as ratio of L (suggest 1/8):1/8

Now we value for rho_zero as ratio of max density

Try 1/4 for light traffic, 3/4 for heavy traffic, and 1/2 for part c

Enter value for rho_zero as ratio of max density (suggest 1/4):1/4

density wave peak starting in the left half

speed of wave is positive

distance travelled = 37.500000 meters

Duration of simulation = 4.000000 seconds

Number of time wave crossed from one half to the other half=1

speed = 9.375000

»

RUN 2 (notice countour matlab problem?)

» nma_problem_7_12

traffic - Program to solve the generalized Burger

equation for the traffic at a stop light problem

solves problem 7.12

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :2

You selected method 2

Enter the number of grid points: (suggest 80):80

Enter value for L, sytem size in meters. (suggest 400) :400

Suggested timestep is 0.2

Enter time step (tau): 0.02

Last car starts moving after 200 steps

Enter number of steps: 200

Maximum density (rho max) suggest 1 :1

Enter value for alpha (suggested 1/5):1/5

Enter value for sigma as ratio of L (suggest 1/8):1/8

Now we value for rho_zero as ratio of max density

Try 1/4 for light traffic, 3/4 for heavy traffic, and 1/2 for part c

Enter value for rho_zero as ratio of max density (suggest 1/4):1/4

density wave peak starting in the left half

speed of wave is positive

distance travelled = 47.500000 meters

Duration of simulation = 4.000000 seconds

Number of time wave crossed from one half to the other half=1

speed = 11.875000

Warning: Reference to uninitialized variable levels in clabel/plus_labels at line 473.

> In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m (plus_labels) at line 473

In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m at line 65

In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW19\nma_problem_7_12.m at line 221

Warning: Reference to uninitialized variable levels in clabel/plus_labels at line 474.

> In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m (plus_labels) at line 474

In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m at line 65

In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW19\nma_problem_7_12.m at line 221

Warning: Reference to uninitialized variable levels in clabel/plus_labels at line 475.

> In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m (plus_labels) at line 475

In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m at line 65

In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW19\nma_problem_7_12.m at line 221

Warning: Reference to uninitialized variable levels in clabel/plus_labels at line 476.

> In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m (plus_labels) at line 476

In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m at line 65

In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW19\nma_problem_7_12.m at line 221

»

RUN 3

» nma_problem_7_12

traffic - Program to solve the generalized Burger

equation for the traffic at a stop light problem

solves problem 7.12

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter the number of grid points: (suggest 80):80

Enter value for L, sytem size in meters. (suggest 400) :400

Suggested timestep is 0.2

Enter time step (tau): 0.02

Last car starts moving after 200 steps

Enter number of steps: 200

Maximum density (rho max) suggest 1 :1

Enter value for alpha (suggested 1/5):1/5

Enter value for sigma as ratio of L (suggest 1/8):1/8

Now we value for rho_zero as ratio of max density

Try 1/4 for light traffic, 3/4 for heavy traffic, and 1/2 for part c

Enter value for rho_zero as ratio of max density (suggest 1/4):1/4

density wave peak starting in the left half

speed of wave is positive

distance travelled = 37.500000 meters

Duration of simulation = 4.000000 seconds

Number of time wave crossed from one half to the other half=1

speed = 9.375000

Warning: Reference to uninitialized variable levels in clabel/plus_labels at line 473.

> In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m (plus_labels) at line 473

In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m at line 65

In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW19\nma_problem_7_12.m at line 221

Warning: Reference to uninitialized variable levels in clabel/plus_labels at line 474.

> In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m (plus_labels) at line 474

In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m at line 65

In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW19\nma_problem_7_12.m at line 221

Warning: Reference to uninitialized variable levels in clabel/plus_labels at line 475.

> In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m (plus_labels) at line 475

In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m at line 65

In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW19\nma_problem_7_12.m at line 221

Warning: Reference to uninitialized variable levels in clabel/plus_labels at line 476.

> In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m (plus_labels) at line 476

In C:\MATLABR11\toolbox\matlab\specgraph\clabel.m at line 65

In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW19\nma_problem_7_12.m at line 221

»

Part b

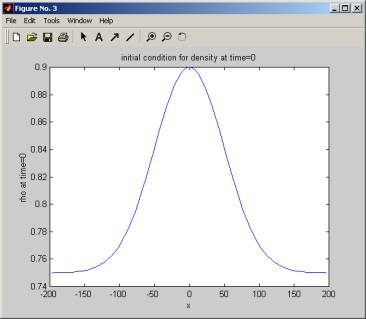
Now repeat the above for HEAVY traffic

Run it 3 times, once per different method. The peak of the density now moves backward. This can be interpreted as this: As cars start to move forward, the point where the peak of the density starts to move backwards since the cars in the back are still standing still while the cars in the front are starting to move. this continues until the last car start to move forward.

RUN 1

» nma_problem_7_12

traffic - Program to solve the generalized Burger

equation for the traffic at a stop light problem

solves problem 7.12

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :1

You selected method 1

Enter the number of grid points: (suggest 80):80

Enter value for L, sytem size in meters. (suggest 400) :400

Suggested timestep is 0.2

Enter time step (tau): 0.02

Last car starts moving after 200 steps

Enter number of steps: 200

Maximum density (rho max) suggest 1 :1

Enter value for alpha (suggested 1/5):1/5

Enter value for sigma as ratio of L (suggest 1/8):1/8

Now we value for rho_zero as ratio of max density

Try 1/4 for light traffic, 3/4 for heavy traffic, and 1/2 for part c

Enter value for rho_zero as ratio of max density (suggest 1/4):3/4

density wave peak starting in the left half

speed of wave is negative

distance travelled = 80.000000 meters

Duration of simulation = 4.000000 seconds

Number of time wave crossed from one half to the other half=0

speed = 20.000000

»

RUN 2

» nma_problem_7_12

traffic - Program to solve the generalized Burger

equation for the traffic at a stop light problem

solves problem 7.12

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :2

You selected method 2

Enter the number of grid points: (suggest 80):80

Enter value for L, sytem size in meters. (suggest 400) :400

Suggested timestep is 0.2

Enter time step (tau): 0.02

Last car starts moving after 200 steps

Enter number of steps: 200

Maximum density (rho max) suggest 1 :1

Enter value for alpha (suggested 1/5):1/5

Enter value for sigma as ratio of L (suggest 1/8):1/8

Now we value for rho_zero as ratio of max density

Try 1/4 for light traffic, 3/4 for heavy traffic, and 1/2 for part c

Enter value for rho_zero as ratio of max density (suggest 1/4):3/4

density wave peak starting in the left half

speed of wave is negative

distance travelled = 60.000000 meters

Duration of simulation = 4.000000 seconds

Number of time wave crossed from one half to the other half=0

speed = 15.000000

»

RUN 3

» nma_problem_7_12

traffic - Program to solve the generalized Burger

equation for the traffic at a stop light problem

solves problem 7.12

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter the number of grid points: (suggest 80):80

Enter value for L, sytem size in meters. (suggest 400) :400

Suggested timestep is 0.2

Enter time step (tau): 0.02

Last car starts moving after 200 steps

Enter number of steps: 200

Maximum density (rho max) suggest 1 :1

Enter value for alpha (suggested 1/5):1/5

Enter value for sigma as ratio of L (suggest 1/8):1/8

Now we value for rho_zero as ratio of max density

Try 1/4 for light traffic, 3/4 for heavy traffic, and 1/2 for part c

Enter value for rho_zero as ratio of max density (suggest 1/4):3/4

density wave peak starting in the left half

speed of wave is negative

distance travelled = 75.000000 meters

Duration of simulation = 4.000000 seconds

Number of time wave crossed from one half to the other half=0

speed = 18.750000

»

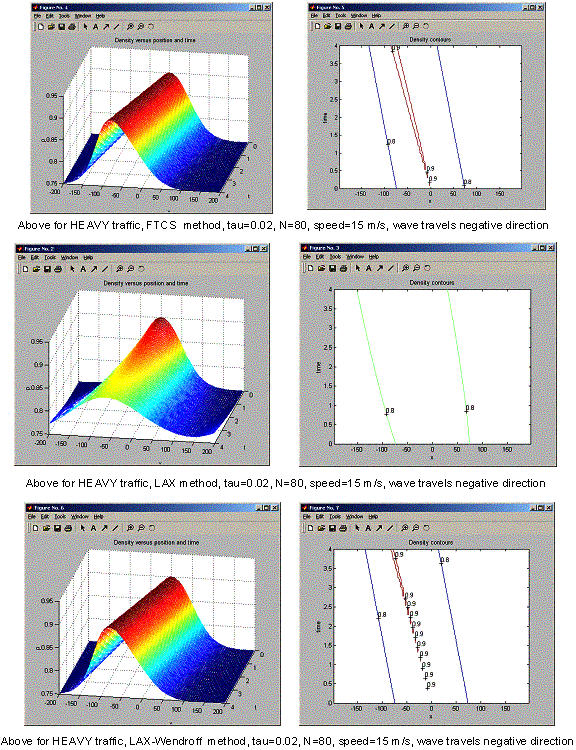
part C

Run the program for Lax-Wendroff, using rho_zero = ½ rho_max.

This show the wave moved very little compared with all the other runs. Speed was only 3m/sec.

» nma_problem_7_12

traffic - Program to solve the generalized Burger

equation for the traffic at a stop light problem

solves problem 7.12

select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :3

You selected method 3

Enter the number of grid points: (suggest 80):80

Enter value for L, sytem size in meters. (suggest 400) :400

Suggested timestep is 0.2

Enter time step (tau): 0.02

Last car starts moving after 200 steps

Enter number of steps: 200

Maximum density (rho max) suggest 1 :1

Enter value for alpha (suggested 1/5):1/5

Enter value for sigma as ratio of L (suggest 1/8):1/8

Now we value for rho_zero as ratio of max density

Try 1/4 for light traffic, 3/4 for heavy traffic, and 1/2 for part c

Enter value for rho_zero as ratio of max density (suggest 1/4):1/2

density wave peak starting in the left half

speed of wave is negative

distance travelled = 15.000000 meters

Duration of simulation = 4.000000 seconds

Number of time wave crossed from one half to the other half=0

speed = 3.750000

»

SOURCE CODE

% traffic - Program to solve the generalized Burger

% equation for the traffic at a stop light problem

% solves problem 7.12

% Nasser Abbasi

clear all; help nma_problem_7_12; % Clear memory and print header

%* Select numerical parameters (time step, grid spacing, etc.).

try_again=1;

while(try_again)

method = input('select numerical method: FTCS=1, Lax=2 Lax-Wendroff=3 :');

if( method<1 | method>3 )

fprintf('Please try again, choice must be 1 or 2 or 3.\n');

else

try_again=0;

fprintf('You selected method %d\n',method);

end

end

N = input('Enter the number of grid points: (suggest 80):');

L = input('Enter value for L, sytem size in meters. (suggest 400) :'); %was 400 System size (meters)

h = L/N; % Grid spacing for periodic boundary conditions

v_max = 25; % Maximum car speed (m/s)

fprintf('Suggested timestep is %g\n',h/v_max);

tau = input('Enter time step (tau): ');

fprintf('Last car starts moving after %g steps\n', ...

(L/4)/(v_max*tau));

nstep = input('Enter number of steps: ');

coeff = tau/(2*h); % Coefficient used by all schemes

coefflw = tau^2/(2*h^2); % Coefficient used by Lax-Wendroff

%* Set initial and boundary conditions

rho_max = input('Maximum density (rho max) suggest 1 :'); % was 1.0 Maximum density

Flow_max = 0.25*rho_max*v_max; % Maximum Flow

%

% input parameters for new initial conditions

%

alpha = input('Enter value for alpha (suggested 1/5):');

sigma = input('Enter value for sigma as ratio of L (suggest 1/8):');

sigma = sigma * L;

fprintf('\nNow we value for rho_zero as ratio of max density\n');

fprintf('Try 1/4 for light traffic, 3/4 for heavy traffic, and 1/2 for part c\n\n');

rho_zero = input('Enter value for rho_zero as ratio of max density (suggest 1/4):');

rho_zero = rho_zero * rho_max;

% Initial condition is a square pulse from x = -L/4 to x = 0

%rho = zeros(1,N);

%for i=round(N/4):round(N/2-1)

% rho(i) = rho_max; % Max density in the square pulse

%end

%rho(round(N/2)) = rho_max/2; % Try running without this line

% Use periodic boundary conditions

ip(1:N) = (1:N)+1; ip(N) = 1; % ip = i+1 with periodic b.c.

im(1:N) = (1:N)-1; im(1) = N; % im = i-1 with periodic b.c.

%* Initialize plotting variables.

iplot = 1;

xplot = ((1:N)-1/2)*h - L/2; % Record x scale for plot

%

% Now find initial condition for density

%

rho = zeros(1,N);

for(i=1:length(xplot))

rho(i) = rho_zero * ( 1 + alpha * exp(- xplot(i)^2 / (2 * sigma^2)));

end

figure;

plot(xplot,rho);

title('initial condition for density at time=0');

xlabel('x');

ylabel('rho at time=0');

rplot(:,1) = rho(:); % Record the initial state

tplot(1) = 0;

figure;

%

% To find the speed of the wave, record the distance travelled by

% the peak of the density. when the simulation is over, we know the

% time it took and hence we find the speed

%

[peak,index]= max(rho);

initialX= xplot(index); % this is where peak density is at start.

if( initialX <= 0 )

fprintf('density wave peak starting in the left half\n');

else

fprintf('density Wave peak starting in the right half\n');

end

signInitialX = initialX;

numberOfFlips = 0;

checkedForDirection = 0; % flag to tell me to find wave direction

direction = 1; % will be set correctly in the loop below.

%* Loop over desired number of steps.

for istep=1:nstep

%* Compute the flow = (Density)*(Velocity)

Flow = rho .* (v_max*(1 - rho/rho_max));

%* Compute new values of density using FTCS,

% Lax or Lax-Wendroff method.

if( method == 1 ) %%% FTCS method %%%

rho(1:N) = rho(1:N) - coeff*(Flow(ip)-Flow(im));

elseif( method == 2 ) %%% Lax method %%%

rho(1:N) = .5*(rho(ip)+rho(im)) ...

- coeff*(Flow(ip)-Flow(im));

else %%% Lax-Wendroff method %%%

cp = v_max*(1 - (rho(ip)+rho(1:N))/rho_max);

cm = v_max*(1 - (rho(1:N)+rho(im))/rho_max);

rho(1:N) = rho(1:N) - coeff*(Flow(ip)-Flow(im)) ...

+ coefflw*(cp.*(Flow(ip)-Flow(1:N)) ...

- cm.*(Flow(1:N)-Flow(im)));

end

%* Record density for plotting.

iplot = iplot+1;

rplot(:,iplot) = rho(:);

tplot(iplot) = tau*istep;

%* Display snap-shot of density versus position

plot(xplot,rho,'-',xplot,Flow/Flow_max,'--');

xlabel('x'); ylabel('Density and Flow');

legend('\rho(x,t)','F(x,t)');

axis([-L/2, L/2, -0.1, 1.1]);

drawnow;

%

% for speed calculation

%

% first find it wave is running clockwise or anti clock wise

% need to check after one istep to find that out

[peak,index]= max(rho);

currentX= xplot(index); % this is where peak density is at now

if( checkedForDirection==0)

checkedForDirection = 1;

if( currentX > initialX )

direction = 1; % 1 means anti clock wise

fprintf('speed of wave is positive\n');

else

direction = 0;

fprintf('speed of wave is negative\n');

end

end

% now record how many time the wave flips around the track

if( (signInitialX * currentX) < 0 )

numberOfFlips = numberOfFlips + 1;

signInitialX= - signInitialX;

end

end

if( initialX <= 0 ) % wave peak started on the left side.

if(direction == 1 ) % anticlock wise

if(currentX >= 0 )

lastPart = currentX + (numberOfFlips-1)*L/2;

else

lastPart = L/2 - abs(currentX) + abs(initialX);

lastPart = lastPArt + (numberOfFlips-1)*L/2;

end

else

if( currentX >= 0 )

lastPart = L/2 - currentX + L/2 - abs(initialX);

lastPart = lastPart + (numberOfFlips-1)*L/2;

else

if( abs(currentX) > abs(initialX))

if(numberOfFlips > 0 )

lastPart = abs(currentX) + L/2 -abs(initialX) + (numberOfFlips-1)*L/2;

else

lastPart = abs(currentX) -abs(initialX);

end

else

lastPart = abs(currentX) + L/2 - abs(initialX) + (numberOfFlips-1)*L/2;

end

end

end

else % initialX on the right half

if( direction == 1 )

if(currentX >= 0 )

lastPart = currentX + (numberOfFlips-1)*L/2

else

lastPart = L/2-InitialX+ L/2- abs(currentX) + (numberOfFlips-1)*L/2;

end

else

if(currentX > 0 )

lastPart = L/2 - currentX + L/2 - initialX + (numberOfFlips-1)*L/2;

else

lastPart = initialX + abs(currentX) + (numberOfFlips-1)*L/2;

end

end

end

speed = lastPart / (istep*tau);

fprintf('distance travelled = %f meters\n',lastPart);

fprintf('Duration of simulation = %f seconds \n',istep*tau);

fprintf('Number of time wave crossed from one half to the other half=%d\n',numberOfFlips);

fprintf('speed = %f\n',speed);

%* Graph density versus position and time as wire-mesh plot

figure; % Clear figure 1 window and bring forward

mesh(tplot,xplot,rplot)

xlabel('t'); ylabel('x'); zlabel('\rho');

title('Density versus position and time');

view([100 30]); % Rotate the plot for better view point

pause(1); % Pause 1 second between plots

%* Graph contours of density versus position and time.

figure; % Clear figure 2 window and bring forward

% Use rot90 function to graph t vs x since

% contour(rplot) graphs x vs t.

clevels = 0:(0.1):1; % Contour levels

cs = contour(xplot,tplot,flipud(rot90(rplot)),clevels);

clabel(cs); % Put labels on contour levels

xlabel('x'); ylabel('time'); title('Density contours');