Problem 8.5
OUTPUT
Conclusion:
|
Grid size |
Number of iterations to reach accuracy |
|
32 x 32 = 1024 points |
108 |
|
64 x 16 = 1024 points |
318 |
|
16 x 64 = 1024 points |
314 |
For same number of grid points (1024 in this case), if the grid is square (hx= hy), then accuracy is reached much faster (in about 30% of the iterations as needed for the other two cases), where one side is 4 times as large as the other.
When the grid is rectangular (one side is 4 times as large), it seems making the x side the smaller side instead of the y side, was a little faster (1%), it saved 4 iterations compared to the case when the x side was the larger side to reach the required accuracy. Not sure why now. I have expected it not to make a difference which is which. May be I made a mistake somewhere?
»
nma_problem_8_5
nma_problem_8_5 - Program to solve the
Laplace equation using
Jacobi on any grid. Modified from teacher
relax.m
Nasser Abbasi
Enter
number of grid points on X side: 32
Enter
number of grid points on Y side: 32
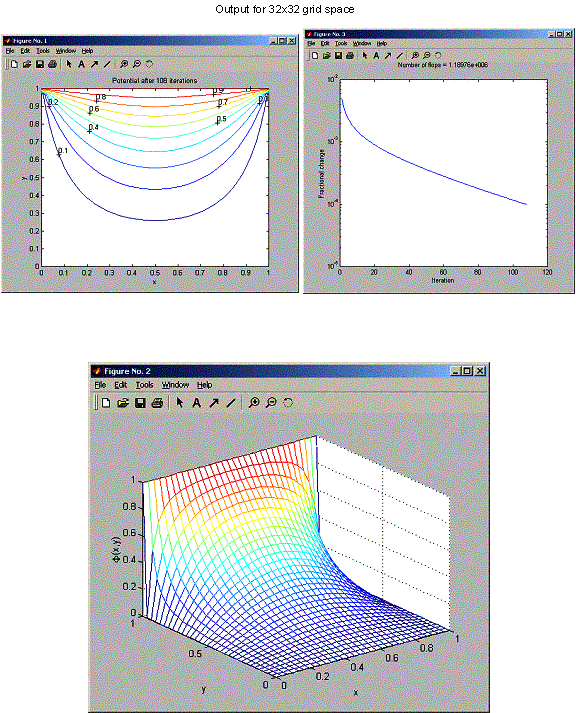
Potential
at y=L equals 1
Potential
is zero on all other boundaries
Desired
fractional change = 0.0001
After
10 iterations, fractional change = 0.001494
After
20 iterations, fractional change = 0.000901622
After
30 iterations, fractional change = 0.000630696
After
40 iterations, fractional change = 0.000468099
After
50 iterations, fractional change = 0.000359621
After
60 iterations, fractional change = 0.00028163
After
70 iterations, fractional change = 0.000223293
After
80 iterations, fractional change = 0.000178636
After
90 iterations, fractional change = 0.000143906
After
100 iterations, fractional change = 0.000116584
Desired
accuracy achieved after 108 iterations
Breaking
out of main loop
» nma_problem_8_5
nma_problem_8_5 - Program to solve the Laplace equation using
Jacobi on any grid. Modified from teacher
relax.m
Nasser Abbasi
Enter
number of grid points on X side: 64
Enter
number of grid points on Y side: 16
Potential
at y=L equals 1
Potential
is zero on all other boundaries
Desired
fractional change = 0.0001
After
10 iterations, fractional change = 0.00453336
After
20 iterations, fractional change = 0.00316517
After
30 iterations, fractional change = 0.00245975
After
40 iterations, fractional change = 0.0020087
After
50 iterations, fractional change = 0.00168657
After
60 iterations, fractional change = 0.00144182
After
70 iterations, fractional change = 0.00124918
After
80 iterations, fractional change = 0.00109325
After
90 iterations, fractional change = 0.000963651
After
100 iterations, fractional change = 0.000854087
After
110 iterations, fractional change = 0.000760386
After
120 iterations, fractional change = 0.000679483
After
130 iterations, fractional change = 0.000609025
After
140 iterations, fractional change = 0.000547333
After
150 iterations, fractional change = 0.000493
After
160 iterations, fractional change = 0.000444915
After
170 iterations, fractional change = 0.00040222
After
180 iterations, fractional change = 0.000364186
After
190 iterations, fractional change = 0.000330169
After
200 iterations, fractional change = 0.000299673
After
210 iterations, fractional change = 0.000272279
After
220 iterations, fractional change = 0.000247597
After
230 iterations, fractional change = 0.000225339
After
240 iterations, fractional change = 0.000205216
After
250 iterations, fractional change = 0.000186986
After
260 iterations, fractional change = 0.000170444
After
270 iterations, fractional change = 0.000155408
After
280 iterations, fractional change = 0.000141727
After
290 iterations, fractional change = 0.000129269
After
300 iterations, fractional change = 0.000117919
After
310 iterations, fractional change = 0.000107573
Desired
accuracy achieved after 318 iterations
Breaking
out of main loop
»

» nma_problem_8_5
nma_problem_8_5 - Program to
solve the Laplace equation using
Jacobi on any grid. Modified from teacher
relax.m
Nasser Abbasi
» nma_problem_8_5
nma_problem_8_5 - Program to solve the
Laplace equation using
Jacobi on any grid. Modified from teacher
relax.m
Nasser Abbasi
Enter
number of grid points on X side: 16
Enter
number of grid points on Y side: 64
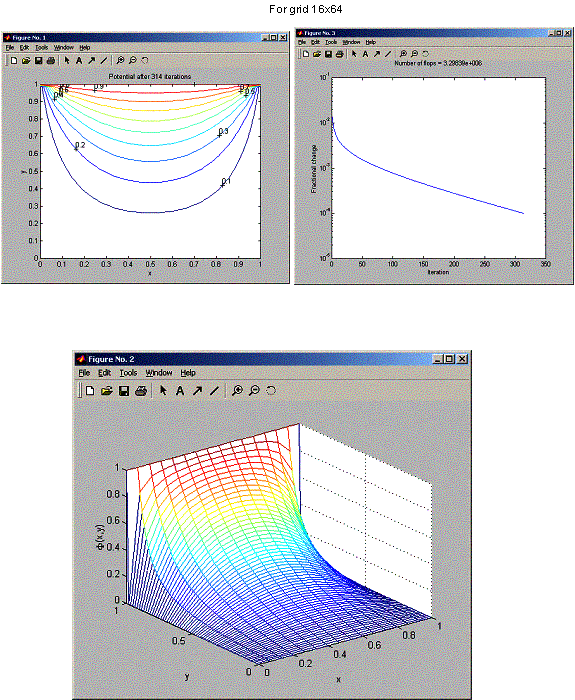
Potential
at y=L equals 1
Potential
is zero on all other boundaries
Desired
fractional change = 0.0001
After
10 iterations, fractional change = 0.00434515
After
20 iterations, fractional change = 0.00293464
After
30 iterations, fractional change = 0.0022554
After
40 iterations, fractional change = 0.00183203
After
50 iterations, fractional change = 0.00153469
After
60 iterations, fractional change = 0.00131098
After
70 iterations, fractional change = 0.00113504
After
80 iterations, fractional change = 0.000992415
After
90 iterations, fractional change = 0.000874214
After
100 iterations, fractional change = 0.000774628
After
110 iterations, fractional change = 0.000689663
After
120 iterations, fractional change = 0.000616464
After
130 iterations, fractional change = 0.000553123
After
140 iterations, fractional change = 0.000498431
After
150 iterations, fractional change = 0.000450142
After
160 iterations, fractional change = 0.000407308
After
170 iterations, fractional change = 0.000369167
After
180 iterations, fractional change = 0.000335102
After
190 iterations, fractional change = 0.00030458
After
200 iterations, fractional change = 0.000277169
After
210 iterations, fractional change = 0.000252489
After
220 iterations, fractional change = 0.000230227
After
230 iterations, fractional change = 0.000210101
After
240 iterations, fractional change = 0.000191881
After
250 iterations, fractional change = 0.000175368
After
260 iterations, fractional change = 0.000160381
After
270 iterations, fractional change = 0.000146736
After
280 iterations, fractional change = 0.000134284
After
290 iterations, fractional change = 0.0001229
After
300 iterations, fractional change = 0.000112478
After
310 iterations, fractional change = 0.000102933
Desired
accuracy achieved after 314 iterations
Breaking
out of main loop
»
CODE
% nma_problem_8_5 - Program to
solve the Laplace equation using
% Jacobi on any grid. Modified
from teacher relax.m
% Nasser Abbasi
clear all; help nma_problem_8_5; % Clear
memory and print header
%* Initialize parameters (system
size, grid spacing, etc.)
Nx = input('Enter
number of grid points on X side: ');
Ny = input('Enter
number of grid points on Y side: ');
L = 1;
% System size (length)
hx = L/(Nx-1);
% Grid spacing X
hy = L/(Ny-1);
% Grid spacing Y
alpha = hy/hx;
beta =
alpha^2;
coef1 = beta/(2*(1+beta));
coef2 = 1/(2*(1+beta));
x = (0:Nx-1)*hx;
% x coordinate
y = (0:Ny-1)*hy;
% y coordinate
%* Set initial guess as first term
in separation of variables soln.
phi0 = 1;
% Potential at y=L
phi = phi0 *
4/(pi*sinh(pi)) * sin(pi*x'/L)*sinh(pi*y/L);
%* Set boundary conditions
phi(1,:) =
0;
phi(Nx,:) = 0;
phi(:,1) =
0;
phi(:,Ny) = phi0*ones(Nx,1);
fprintf('Potential at
y=L equals %g \n',phi0);
fprintf('Potential is
zero on all other boundaries\n');
%* Loop until desired fractional
change per iteration is obtained
flops(0); % Reset the flops
counter to zero;
newphi =
phi; %
Copy of the solution (used only by Jacobi)
iterMax = max(Ny^2,Nx^2); % Set max to avoid
excessively long runs
changeDesired = 1e-4; % Stop when the change is given
fraction
fprintf('Desired
fractional change = %g\n',changeDesired);
for iter =1:iterMax
changeSum
= 0;
for i=2:(Nx-1)
% Loop over interior points only
for j=2:(Ny-1)
% newphi(i,j) =
.25*(phi(i+1,j)+phi(i-1,j)+ ...
%
phi(i,j-1)+phi(i,j+1));
newphi(i,j) = coef1*(phi(i+1,j)+phi(i-1,j))+ ...
coef2*(phi(i,j-1)+phi(i,j+1));
changeSum = changeSum + abs(1-phi(i,j)/newphi(i,j));
end
end
phi =
newphi;
%* Check if fractional change is small enough to halt
the iteration
change(iter) = max(changeSum/(Ny-2)^2, changeSum/(Nx-2)^2);
%change(iter) = changeSum/(Ny-2)^2;
if( rem(iter,10) < 1 )
fprintf('After %g iterations, fractional
change = %g\n',...
iter,change(iter));
end
if( change(iter) < changeDesired )
fprintf('Desired accuracy achieved after
%g iterations\n',iter);
fprintf('Breaking
out of main loop\n');
break;
end
end
%* Plot final estimate of
potential as contour and surface plots
figure(1); clf;
cLevels = 0:(0.1):1; % Contour levels
cs = contour(x,y,flipud(rot90(phi)),cLevels);
xlabel('x');
ylabel('y'); clabel(cs);
title(sprintf('Potential
after %g iterations',iter));
figure(2); clf;
mesh(x,y,flipud(rot90(phi)));
xlabel('x');
ylabel('y'); zlabel('\Phi(x,y)');
%* Plot the fractional change
versus iteration
figure(3); clf;
semilogy(change);
xlabel('Iteration'); ylabel('Fractional
change');
title(sprintf('Number
of flops = %g\n',flops));