HW 21, problem 10.12

Nasser Abbasi

OUTPUT:

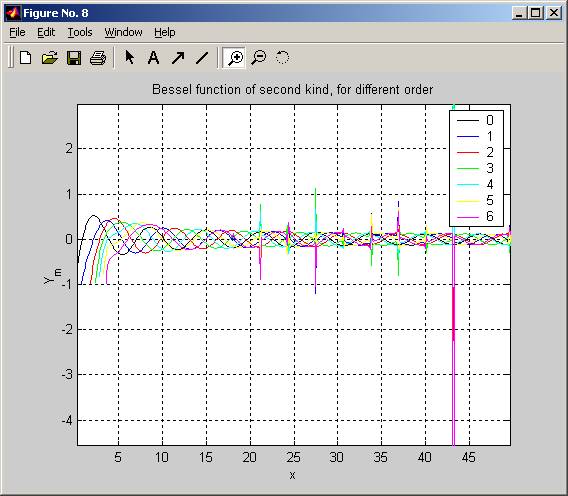
I plot Bessel functions of second kind for order 0,1,2,3,4,5,6.

Plot each Bessel function in separate plot, then all on the same plot. The x range used is 0.1 up to 49.9.

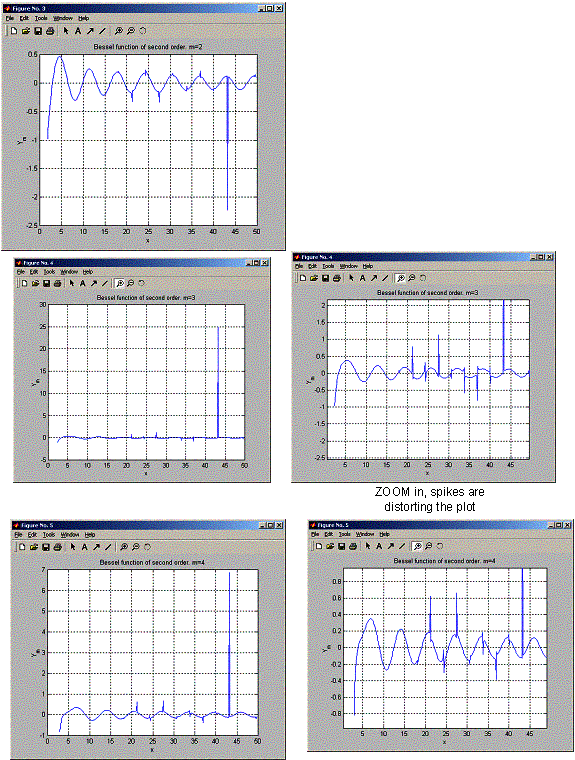
Used matlab zoom to show the plots for different smaller x range to make it clearer.

To find J0 and J1, I used matlab besselj.

One thing I noticed is that there is some sort of discontinuity in Y_1, it starts at around x=21.1, so below x=21 the plots look close to matlab own implementation, but then I started seeing these spikes in the plots. Was not able to determine why. Next, I used matlab own bessely function to plot the functions to compare my output to matlab.

I suspect something wrong in my implementation of the formula to find Y1 from Y0

J1 * Y0 – J0 * Y1 = 2/Pi*x

From the above, I find Y1 = J1 * Y0/J0 - 2/(Pi * x * J0)

Then use the main recursive formula to find Y2, Y3, etc…. So if Y1 is not exact, this effect will carry over.

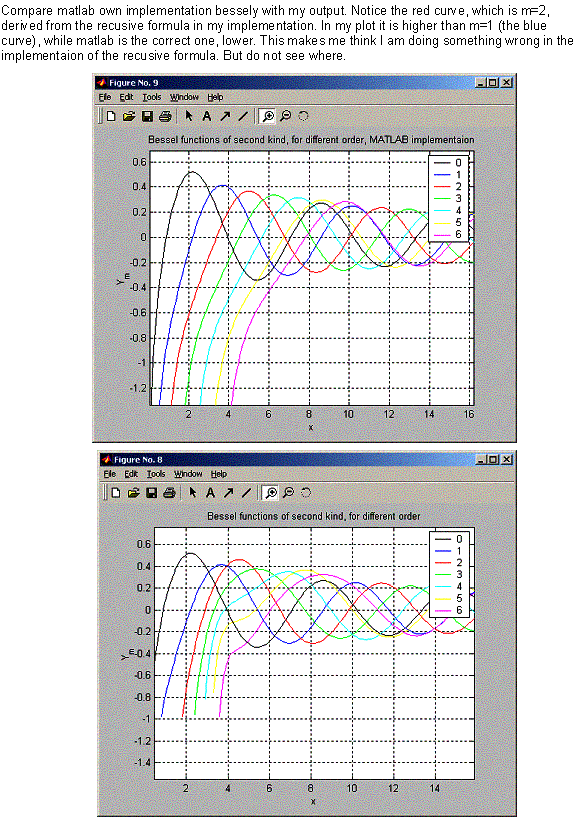
Now I show each Bessel function on separate plot. Used zoom to display closer plots.

CODE:

function nma_problem_10_12

%

% program to solve problem 8.12 in book

% finds Bessel functions of second kind.

%

% By Nasser Abbasi

%

% uses besselj.m for finding bessel functions of first kind.

%

clear all; help nma_problem_10_12;

% set up the x points

x = 0.1:0.1:49.9;

%

% for simplicty, first I find Y_0 and Y_1 over all the x domain

% then loop again over x to find all the other Y's using the

% recursive equation.

%

maxM=6; % pick some max m to plot for.

%

% reserve space for the Ym matrix. each column in this matrix

% represent Y_m. For column 1 is Y_0, column 2 is Y_1, etc...

% so number of columns goes from 1..m-1

% The number of rows is the number of x points the Y's are evaluated

% at.

%

Y=zeros(length(x),maxM+1); % i.e. order=0,1,2,3,4,5,6

for(i = 1:length(x) )

Y(i,1) = getYZero( x(i) );

Y(i,2) = getYOne( x(i) , Y(i,1) );

end

%

% Now find the rest of the bessel functions

%

for(m=2:maxM+1)

for(i = 1:length(x) )

Y(i,m+1) = (2*m/x(i)) * Y(i,m) - Y(i,m-1);

end

end

myLegend=['k' 'b' 'r' 'g' 'c' 'y' 'm'];

legendTags=struct('legendTag','');

%

% plot each bessel function on separat plot for debugging,

% then plot them all on the same plot

for(m=1:maxM+1)

%

% to print all Y_m on the same plot, I found I need

% to limit the value of the functions to about -1 on the

% y axis, to make things show clearly.

[X_,Y_] = getTrimmedY(x,Y(:,m));

figure;

plot(X_,Y_);

title(sprintf('Bessel function of second order. m=%d',m-1));

xlabel('x');

ylabel('Y_m');

grid on;

end

figure;

for(m=1:maxM+1)

%

% to print all Y_m on the same plot, I found I need

% to limit the value of the functions to about -1 on the

% y axis, to make things show clearly.

[X_,Y_] = getTrimmedY(x,Y(:,m));

plot(X_,Y_,myLegend(m));

legendTags(m).legendTag=sprintf('%d',m-1);

hold on;

end

title('Bessel functions of second kind, for different order');

xlabel('x');

ylabel('Y_m');

legend(legendTags(1:maxM+1).legendTag);

grid on;

%

% plot it using matlab bessely to compare

%

figure;

for(m=1:maxM+1)

Y(:,m) = bessely(m-1,x(1:end))';

plot(x,Y(:,m),myLegend(m));

hold on;

end

title('Bessel functions of second kind, for different order, MATLAB implementaion');

xlabel('x');

ylabel('Y_m');

legend(legendTags(1:maxM+1).legendTag);

grid on;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [x_,y_] = getTrimmedY(x,y)

for(i=1:length(x))

if( y(i) > -1 )

x_ = x(i:end);

y_ = y(i:end);

return;

end

end

x_ = x;

y_ = y;

%%%%%%%%%%%%%%%%%%%%%%%%%5

%

%

%%%%%%%%%%%%%%%%%%%%%%%%%%

function v=getYZero(x)

lambda = 0.577215664;

maxK = 10; % 10 terms for the sum should be enough

sum=0;

for(k = 1:maxK )

sum = sum + ( (-1)^k * (1/k) * besselj(2*k,x) );

end

v = (2/pi) * ( log(x/2) + lambda ) * besselj(0,x) - ( (4/pi) * sum );

return;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function v=getYOne(x,Y0)

v = besselj(1,x)* Y0 / besselj(0,x) ;

v = v - ( 2/(pi*x*besselj(0,x)) );