Problem 8.8
Nasser Abbasi
OUTPUT
Part a was run with and without Faraday cage. Then part b and c ran with faraday cage present. (running part b and c without the faraday cage present is not needed as it is is the same as running part a without the faraday cage, since nothing else would have changed).
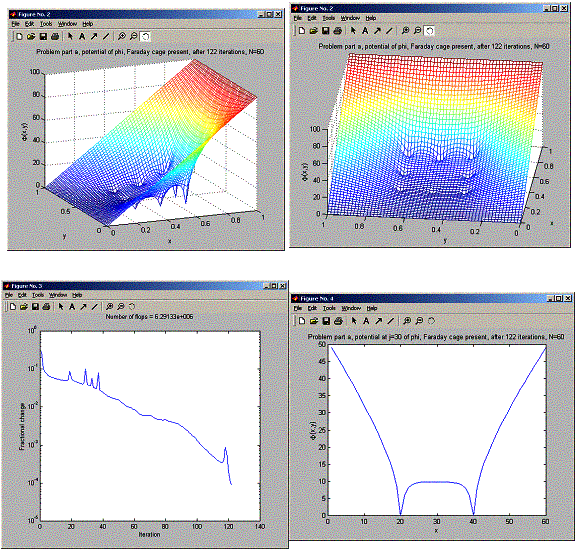
For part a, when running with faraday cage present, the potential at the j=30 line had value of about 10 between the left and right faraday points (20,30) and (40,30).
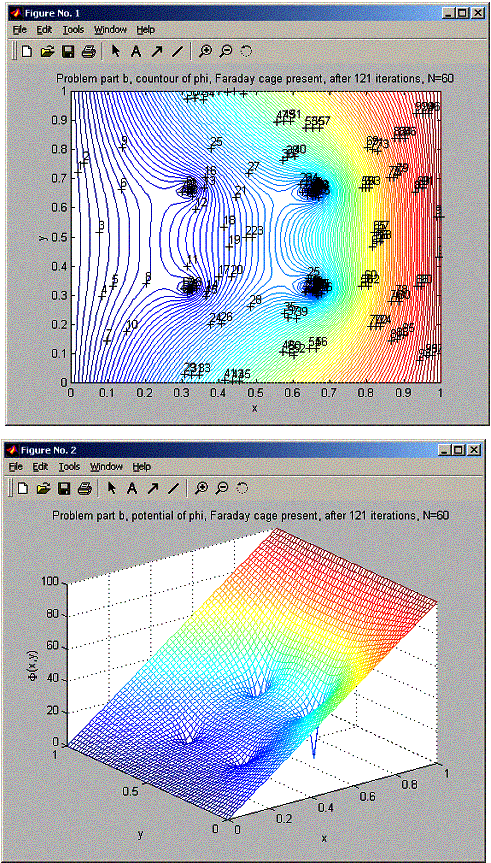
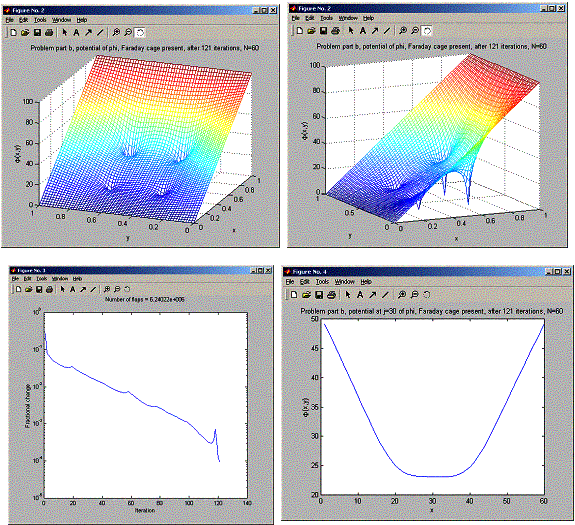
For part b, the potential at the j=30 line had a value of about 18 between the same two points as above. This is because less points are now at zero potential, and the 4 points that are at zero potential are the corner points.
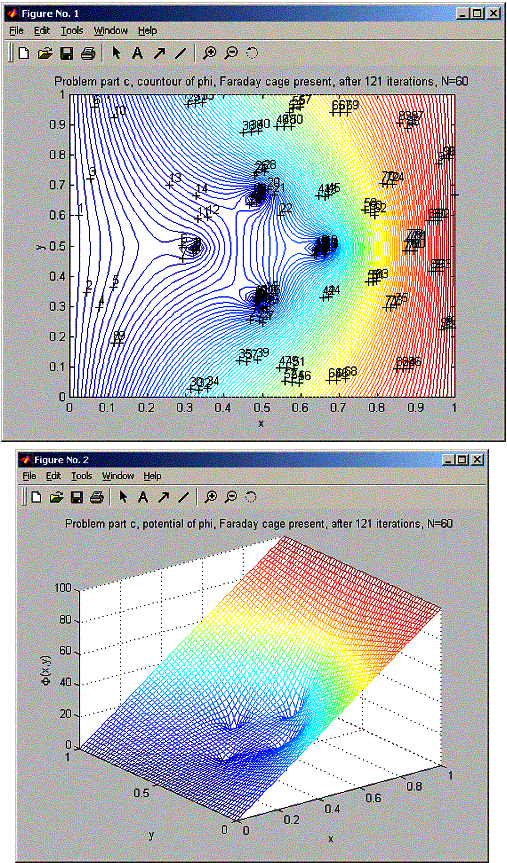
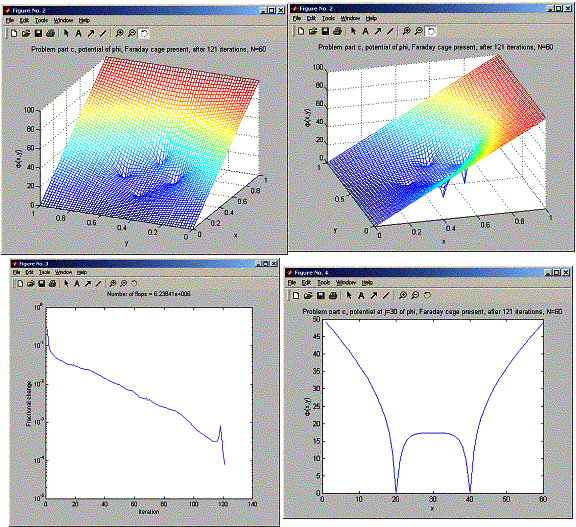
For part c, The shape of the potential at the j=30 line looks the same as for part a, but the value is higher in the middle of the two points. About the same as part b above (since the same number of points). So it looks like the average potential at the middle of the faraday cage is the same if the number of points is the same and does not depend on the orientation of the cage, but depends on the number of faraday points that are potential zero.
When the number of points at zero is 8, potential in the center of the cage was about 10.
When the number of points at zero is 4, potential in the center of the cage was about 18.
Without the faraday cage present, the potential at the line j=30 is almost constant (as what one would expect) . this can be seen from the plot.
Run part a, with Faraday cage present
» nma_problem_8_8
nma_problem_8_8 - Program to solve problem 8.8 in book
Enter number of grid points on a side: 60
Enter problem part to solve (a=1, b=2, c=3):1
Should I apply Faraday cage? [1=Yes, 0=NO] :1
Theoretical optimum omega = 1.90053
Enter desired omega: 1.9
Potential at y=L equals 100
Desired fractional change = 0.0001
After 10 iterations, fractional change = 0.0565377
After 20 iterations, fractional change = 0.0558858
After 30 iterations, fractional change = 0.0385277
After 40 iterations, fractional change = 0.0239683
After 50 iterations, fractional change = 0.0154008
After 60 iterations, fractional change = 0.00844819
After 70 iterations, fractional change = 0.00611628
After 80 iterations, fractional change = 0.0046467
After 90 iterations, fractional change = 0.00316189
After 100 iterations, fractional change = 0.00131194
After 110 iterations, fractional change = 0.000508721
After 120 iterations, fractional change = 0.000196511
Desired accuracy achieved after 122 iterations
Breaking out of main loop

Run part a, with NO Faraday cage present
» nma_problem_8_8
nma_problem_8_8 - Program to solve problem 8.8 in book
Enter number of grid points on a side: 60
Enter problem part to solve (a=1, b=2, c=3):1
Should I apply Faraday cage? [1=Yes, 0=NO] :0
Theoretical optimum omega = 1.90053
Enter desired omega: 1.9
Potential at y=L equals 100
Desired fractional change = 0.0001
After 10 iterations, fractional change = 0.0356929
After 20 iterations, fractional change = 0.0204735
After 30 iterations, fractional change = 0.0121423
After 40 iterations, fractional change = 0.00718592
After 50 iterations, fractional change = 0.00473539
After 60 iterations, fractional change = 0.00414818
After 70 iterations, fractional change = 0.00246191
After 80 iterations, fractional change = 0.00153293
After 90 iterations, fractional change = 0.000889489
After 100 iterations, fractional change = 0.000505454
After 110 iterations, fractional change = 0.000293859
After 120 iterations, fractional change = 7.26886e-005
Desired accuracy achieved after 120 iterations
Breaking out of main loop
»

Run part b, with Faraday cage present
» nma_problem_8_8
nma_problem_8_8 - Program to solve problem 8.8 in book
Enter number of grid points on a side: 60
Enter problem part to solve (a=1, b=2, c=3):2
Should I apply Faraday cage? [1=Yes, 0=NO] :1
Theoretical optimum omega = 1.90053
Enter desired omega: 1.9
Potential at y=L equals 100
Desired fractional change = 0.0001
After 10 iterations, fractional change = 0.0403522
After 20 iterations, fractional change = 0.0334746
After 30 iterations, fractional change = 0.0196417
After 40 iterations, fractional change = 0.0129768
After 50 iterations, fractional change = 0.00788112
After 60 iterations, fractional change = 0.00638972
After 70 iterations, fractional change = 0.00337059
After 80 iterations, fractional change = 0.00265851
After 90 iterations, fractional change = 0.00163381
After 100 iterations, fractional change = 0.000997667
After 110 iterations, fractional change = 0.000423025
After 120 iterations, fractional change = 0.000122452
Desired accuracy achieved after 121 iterations
Breaking out of main loop
»
Run part c, with Faraday cage present
» nma_problem_8_8
nma_problem_8_8 - Program to solve problem 8.8 in book
Enter number of grid points on a side: 60
Enter problem part to solve (a=1, b=2, c=3):3
Should I apply Faraday cage? [1=Yes, 0=NO] :1
Theoretical optimum omega = 1.90053
Enter desired omega: 1.9
Potential at y=L equals 100
Desired fractional change = 0.0001
After 10 iterations, fractional change = 0.0415334
After 20 iterations, fractional change = 0.0295801
After 30 iterations, fractional change = 0.0226194
After 40 iterations, fractional change = 0.0143339
After 50 iterations, fractional change = 0.00980936
After 60 iterations, fractional change = 0.00597052
After 70 iterations, fractional change = 0.00393774
After 80 iterations, fractional change = 0.00246038
After 90 iterations, fractional change = 0.00176095
After 100 iterations, fractional change = 0.000760914
After 110 iterations, fractional change = 0.000382697
After 120 iterations, fractional change = 0.000156384
Desired accuracy achieved after 121 iterations
Breaking out of main loop
»
Source code
function nma_problem_8_8()
%
nma_problem_8_8 - Program to solve problem 8.8 in book
clear all; help
nma_problem_8_8; % Clear memory and print header
%*
Initialize parameters (system size, grid spacing, etc.)
N = input('Enter number of grid points on a side: ');
L = 1; %
System size (length)
h = L/(N-1); % Grid
spacing
x = (0:N-1)*h; % x
coordinate
y = (0:N-1)*h; % y
coordinate
problemPart = input('Enter problem part to solve (a=1, b=2, c=3):');
useFaraday = input('Should
I apply Faraday cage? [1=Yes, 0=NO] :');
%*
Select over-relaxation factor (SOR only)
omegaOpt =
2/(1+sin(pi/N)); % Theoretical optimum
fprintf('Theoretical optimum omega = %g \n',omegaOpt);
omega = input('Enter
desired omega: ');
%* Set
initial guess as first term in separation of variables soln.
phi0 = 100; %
Potential at y=L
phi = phi0 * 4/(pi*sinh(pi)) *
sin(pi*x'/L)*sinh(pi*y/L);
%* Set
boundary conditions
% to map
these to physical grid, think of what
% it
will be after flipud and rot90 is applied to phi.
%
phi(1,:) = 0; % this is
the LEFT wall
phi(N,:) = 100; % this is
the RIGHT wall
slope = 100/L;
for(i=1:N)
phi(i,1) = slope*(i-1)*h;
% this is the BOTTOM wall
end
for(i=1:N)
phi(i,N) = slope*(i-1)*h;
% this is the TOP wall
end
fprintf('Potential at y=L equals %g \n',phi0);
%fprintf('Potential
is zero on all other boundaries\n');
%* Loop
until desired fractional change per iteration is obtained
flops(0); %
Reset the flops counter to zero;
iterMax = N^2; %
Set max to avoid excessively long runs
changeDesired = 1e-4; % Stop when
the change is given fraction
fprintf('Desired fractional change = %g\n',changeDesired);
for iter
= 1:iterMax
changeSum = 0;
for i = 2:(N-1) % Loop
over interior points only
for j = 2:(N-1)
if(
isFaradayPoint(i,j,useFaraday,problemPart))
newphi=0;
else
newphi = 0.25*omega*(phi(i+1,j)+phi(i-1,j)+ ...
phi(i,j-1)+phi(i,j+1)) + (1-omega)*phi(i,j);
changeSum = changeSum + abs(1-phi(i,j)/newphi);
end
phi(i,j) = newphi;
end
end
%* Check if fractional change
is small enough to halt the iteration
change(iter) = changeSum/(N-2)^2;
if( rem(iter,10) < 1 )
fprintf('After %g iterations,
fractional change = %g\n',...
iter,change(iter));
end
if( change(iter) <
changeDesired )
fprintf('Desired accuracy
achieved after %g iterations\n',iter);
fprintf('Breaking out of main loop\n');
break;
end
end
%* Plot
final estimate of potential as contour and surface plots
%
convert the memory matlab matrix layout to the physical grid layout
phi = phi';
figure;
cLevels = 0:1:100; % Contour
levels
%cs =
contour(x,y,flipud(rot90(phi)),cLevels);
cs =
contour(x,y,phi,cLevels);
xlabel('x'); ylabel('y');
clabel(cs);
title(makeTitle('countour',useFaraday,iter,N,problemPart));
figure;
%mesh(x,y,flipud(rot90(phi)));
mesh(x,y,phi);
xlabel('x'); ylabel('y');
zlabel('\Phi(x,y)');
title(makeTitle('potential',useFaraday,iter,N,problemPart));
%* Plot
the fractional change versus iteration
figure;
semilogy(change);
xlabel('Iteration');
ylabel('Fractional change');
title(sprintf('Number of flops = %g\n',flops));
% plot
the potential at i=30
figure;
plot(phi(:,30));
xlabel('x');
ylabel('\Phi(x,y)');
title(makeTitle('potential at j=30',useFaraday,iter,N,problemPart));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% takes
i,j and determines if it is
% a
faraday point depending on which part
% of the
problem we are solving
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function v =
isFaradayPoint(i,j,useFaraday,problemPart)
if(
~useFaraday)
v=0;
return;
end
if(problemPart
== 1 ) % part a
if( (i==20 & j==20) | ...
(i==20 & j==30)
| ...
(i==20 & j==40)
| ...
(i==30 &
j==20) | ...
(i==30 & j==40)
| ...
(i==40 & j==20)
| ...
(i==40 & j==30)
| ...
(i==40 & j==40))
v=1;
else
v=0;
end
return;
end
if(problemPart
== 2 ) % part b
if( (i==20 & j==20) | ...
(i==20 & j==40) |
...
(i==40 & j==20) |
...
(i==40 & j==40))
v=1;
else
v=0;
end
return;
end
if(problemPart
== 3 ) % part c
if( (i==20 & j==30) | ...
(i==30 & j==20) |
...
(i==40 & j==30) |
...
(i==30 & j==40))
v=1;
else
v=0;
end
return;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% helper
function to format title of plot
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function title_
= makeTitle(name,useFaraday,iter,N,problemPart)
if(useFaraday)
useFaraday='Faraday cage present';
else
useFaraday='Faraday cage NOT
present';
end
if(problemPart
== 1 )
problemPart='part a';
elseif problemPart==2
problemPart='part b';
else
problemPart= 'part c';
end
title_ = sprintf('Problem %s, %s of phi, %s, after %d iterations, N=%d',...
problemPart,name,useFaraday,iter,N);
return;