Problem 10.13

Nasser Abbasi

Output

I run Romberg integration for max of 15 iterations.

Part (a)

Exact answer for this part is exp(1)-1.

» nma_problem_10_13

program to solve problem 10.13

Nasser Abbasi

enter problem part [a,b,c,d,e,f]:'a'

Roomberg diagonal values for part a, Exact solution = 1.7182818284590

Row 1, diagonal element = 1.8591409142295

Row 2, diagonal element = 1.7188611518766

Row 3, diagonal element = 1.7182826879248

Row 4, diagonal element = 1.7182818287945

Row 5, diagonal element = 1.7182818284591

Row 6, diagonal element = 1.7182818284590

Row 7, diagonal element = 1.7182818284590

Row 8, diagonal element = 1.7182818284590

Row 9, diagonal element = 1.7182818284590

Row 10, diagonal element = 1.7182818284590

Row 11, diagonal element = 1.7182818284590

Row 12, diagonal element = 1.7182818284590

Row 13, diagonal element = 1.7182818284590

Row 14, diagonal element = 1.7182818284590

Row 15, diagonal element = 1.7182818284591

»

The above shows the absErr is becoming less and less but after iteration 5, no more improvement is seen, and we see the absErr increasing very little when iterations become large (14 and 15).

Part (b)

The exact answer to this is ¾ PI.

> plot( (sin(8*x))^4,x=0..2*Pi);

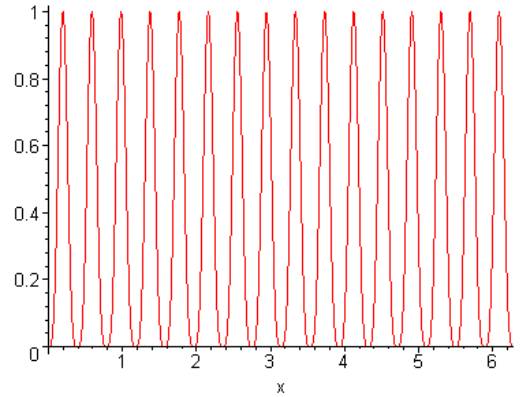
» nma_problem_10_13

program to solve problem 10.13

Nasser Abbasi

enter problem part [a,b,c,d,e,f]:'b'

Roomberg diagonal values for part b, Exact solution = 2.3561944901923

Row 1, diagonal element = 0.0000000000000

Row 2, diagonal element = 0.0000000000000

Row 3, diagonal element = 0.0000000000000

Row 4, diagonal element = 0.0000000000000

Row 5, diagonal element = 0.0000000000000

Row 6, diagonal element = 4.5612183751723

Row 7, diagonal element = 1.9013430443026

Row 8, diagonal element = 2.3827353809869

Row 9, diagonal element = 2.3557875435276

Row 10, diagonal element = 2.3561960721608

Row 11, diagonal element = 2.3561944886493

Row 12, diagonal element = 2.3561944901927

Row 13, diagonal element = 2.3561944901923

Row 14, diagonal element = 2.3561944901923

Row 15, diagonal element = 2.3561944901923

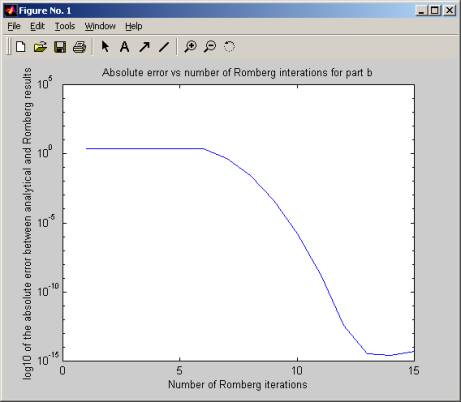
In this, Romberg was actually giving zero as the answer, until iteration 6. So Romberg was way off in this one for the first 6-8 iterations. Then it got closer to the exact answer as the number of iterations increased. But again notice at iteration 15, the absError actually increased a little.

Part (C )

Exact solution here is 2/3

> plot( sqrt(x),x=0..1);

» nma_problem_10_13

program to solve problem 10.13

Nasser Abbasi

enter problem part [a,b,c,d,e,f]:'c'

Roomberg diagonal values for part c, Exact solution = 0.6666666666667

Row 1, diagonal element = 0.5000000000000

Row 2, diagonal element = 0.6380711874577

Row 3, diagonal element = 0.6577566032816

Row 4, diagonal element = 0.6636075691123

Row 5, diagonal element = 0.6655928651295

Row 6, diagonal element = 0.6662876990338

Row 7, diagonal element = 0.6665327411999

Row 8, diagonal element = 0.6666193221483

Row 9, diagonal element = 0.6666499283187

Row 10, diagonal element = 0.6666607488083

Row 11, diagonal element = 0.6666645743914

Row 12, diagonal element = 0.6666659269360

Row 13, diagonal element = 0.6666664051324

Row 14, diagonal element = 0.6666665742003

Row 15, diagonal element = 0.6666666339749

»

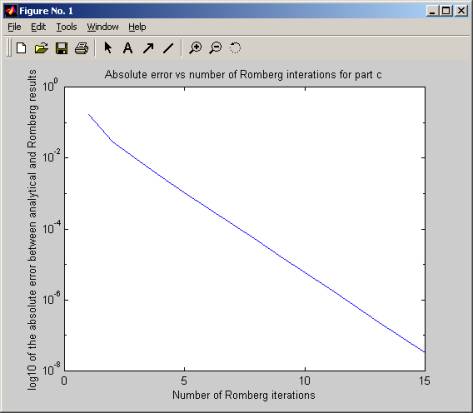
This part showed the abs errors always decreases as iteration is increased. This is because the absError is still not large enough for round off error (for double, need to reach 10^-14 or more for round off to kick in).

Part (d)

Exact answer for this part is PI/4

> plot( sqrt(1-x^2),x=0..1);

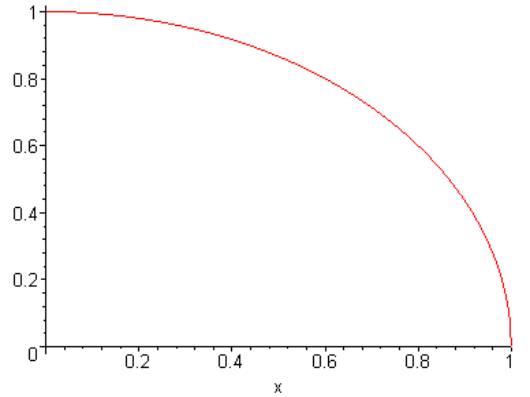
» nma_problem_10_13

program to solve problem 10.13

Nasser Abbasi

enter problem part [a,b,c,d,e,f]:'d'

Roomberg diagonal values for part d, Exact solution = 0.7853981633974

Row 1, diagonal element = 0.5000000000000

Row 2, diagonal element = 0.7440169358563

Row 3, diagonal element = 0.7726909122621

Row 4, diagonal element = 0.7810545410576

Row 5, diagonal element = 0.7838765458406

Row 6, diagonal element = 0.7848616873345

Row 7, diagonal element = 0.7852086696293

Row 8, diagonal element = 0.7853311914173

Row 9, diagonal element = 0.7853744888423

Row 10, diagonal element = 0.7853897937591

Row 11, diagonal element = 0.7853952043810

Row 12, diagonal element = 0.7853971172439

Row 13, diagonal element = 0.7853977935293

Row 14, diagonal element = 0.7853980326298

Row 15, diagonal element = 0.7853981171642

This part is similar to part c. It showed the abs errors always decreases as iteration is increased. This is because the absError is still not large enough for round off error (for double, need to reach 10^-14 or more for round off to kick in).

Part e

Use Maple to help me find P10 using equation 10.15 in book:

> P10 := %;

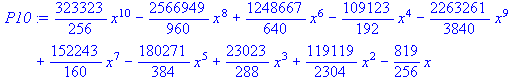
> plot(P10,x=-1..1);

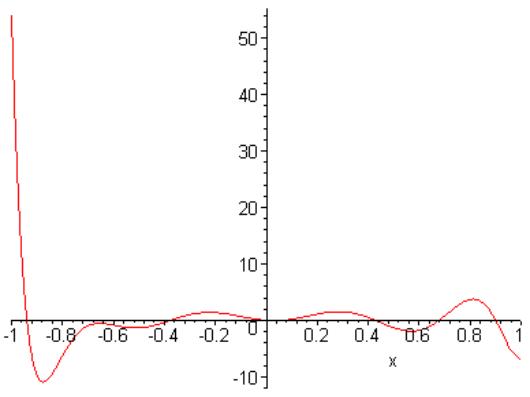
The exact integral is 0 of P10 from –1..1

> int(P10,x=-1..1);

>

» nma_problem_10_13

program to solve problem 10.13

Nasser Abbasi

enter problem part [a,b,c,d,e,f]:'e'

Roomberg diagonal values for part e, Exact solution = 0.0000000000000

Row 1, diagonal element = 46.9388888888892

Row 2, diagonal element = 15.6462962962964

Row 3, diagonal element = 5.4198629195602

Row 4, diagonal element = 4.2572827826606

Row 5, diagonal element = 0.1868756612142

Row 6, diagonal element = 0.0000000000000

Row 7, diagonal element = 0.0000000000000

Row 8, diagonal element = 0.0000000000000

Row 9, diagonal element = 0.0000000000000

Row 10, diagonal element = 0.0000000000000

Row 11, diagonal element = 0.0000000000000

Row 12, diagonal element = 0.0000000000000

Row 13, diagonal element = 0.0000000000000

Row 14, diagonal element = 0.0000000000000

Row 15, diagonal element = 0.0000000000000

»

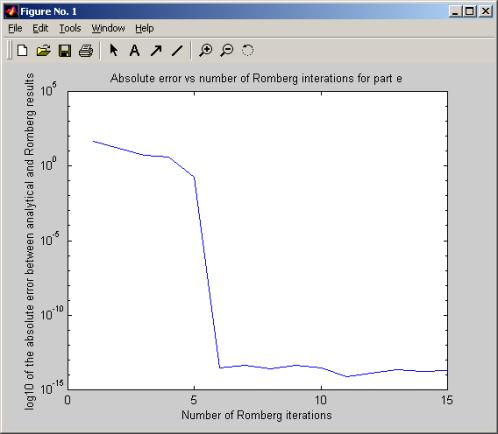
This showed that the abs error decreased as number of iterations reached 6 very quickly, then abs error remained unchanged as number of iterations is increased more, although at about iteration 12 I see small increase.

Part (f)

This is the same as part e, but square the legendre polynomial. Since squared function, will have no negative values, so we should expect an area to be positive.

> plot((P10)^2,x=-1..1);

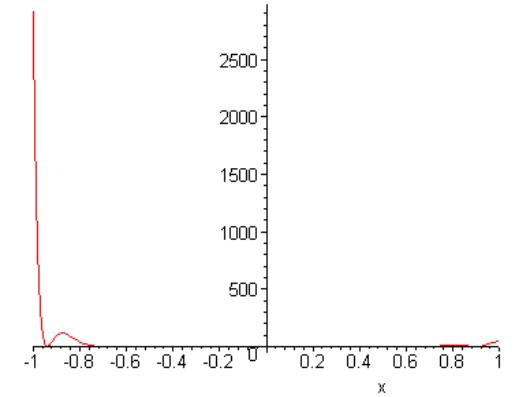
> int(P10^2,x=-1..1);

» nma_problem_10_13

program to solve problem 10.13

Nasser Abbasi

enter problem part [a,b,c,d,e,f]:'f'

Roomberg diagonal values for part f, Exact solution =59.7690001151112

Row 1, diagonal element = 2972.6500308642235

Row 2, diagonal element = 990.8833436214079

Row 3, diagonal element = 464.9019967094017

Row 4, diagonal element = 234.6787608206562

Row 5, diagonal element = 137.6807502193288

Row 6, diagonal element = 69.6008330666823

Row 7, diagonal element = 59.9362358893052

Row 8, diagonal element = 59.7693433957478

Row 9, diagonal element = 59.7690001928081

Row 10, diagonal element = 59.7690001151129

Row 11, diagonal element = 59.7690001151115

Row 12, diagonal element = 59.7690001151116

Row 13, diagonal element = 59.7690001151116

Row 14, diagonal element = 59.7690001151115

Row 15, diagonal element = 59.7690001151115

»

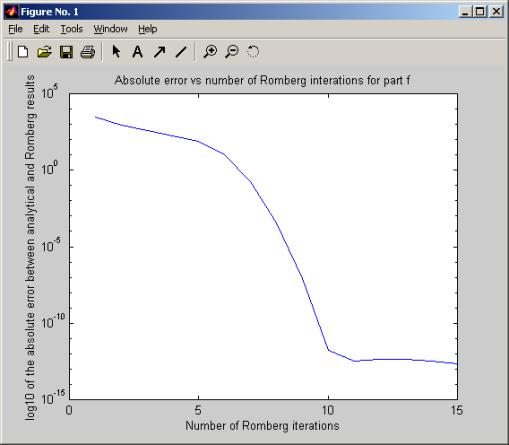
compare this to part e, we see it took more Romberg iterations to zoom in to the exact solution.

CODE:

function nma_problem_10_13

%

% program to solve problem 10.13

% Nasser Abbasi

clear all; help nma_problem_10_13;

format long g;

part = input('enter problem part [a,b,c,d,e,f]:');

switch part

case 'a'

% integrate: exp(x) from x=0..1) ;

exactAnswer = exp(1)-1;

[absErr,RombergTable] = process(exactAnswer,'exp',0,1);

case 'b'

% integrate (sin(8 x)^4) from x=0..2PI

exactAnswer = (3/4)*pi;

[absErr,RombergTable] = process(exactAnswer,'partb',0,2*pi);

case 'c'

% integrate (sqrt(x)) from x=0..1

exactAnswer = 2/3;

[absErr,RombergTable] = process(exactAnswer,'partc',0,1);

case 'd'

% integrate (sqrt( 1-x^2)) from x=0..1

exactAnswer = pi/4;

[absErr,RombergTable] = process(exactAnswer,'partd',0,1);

case 'e'

%integrate P10 from -1..1

exactAnswer = 0;

[absErr,RombergTable] = process(exactAnswer,'parte',-1,1);

case 'f'

%integrate P10^2 from -1..1

exactAnswer = 415382597/6949800;

[absErr,RombergTable] = process(exactAnswer,'partf',-1,1);

end

semilogy(absErr,'-');

title(sprintf('Absolute error vs number of Romberg interations for part %s',part));

xlabel('Number of Romberg iterations');

ylabel('log10 of the absolute error between analytical and Romberg results');

fprintf('Roomberg diagonal values for part %s, Exact solution =%16.13f\n',part,exactAnswer);

for(i=1:length(RombergTable))

fprintf('Row %d, diagonal element = %16.13f\n',i,RombergTable(i,i));

end

%%%%%%%%%%%%%%%%%%%%%%5

%

%

%%%%%%%%%%%%%%%%%%%%%%%%

function [absErr,RombergTable]=process(exactAnswer,fun,lowerLimit,upperLimit)

maxIter=15;

i=0;

while( i< maxIter )

i=i+1;

RombergTable = rombf(lowerLimit,upperLimit,i,fun);

absErr(i) = abs(RombergTable(i,i)-exactAnswer);

end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function v=partb(x)

v= sin(8*x);

v= v^4;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function v=partc(x)

v=real(sqrt(x));

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function v=partd(x)

v=real(sqrt(1-x^2));

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function v=parte(x)

v=323323/256*x^10-2566949/960*x^8+...

1248667/640*x^6-109123/192*x^4-2263261/3840*x^9+...

152243/160*x^7-180271/384*x^5+23023/288*x^3+...

119119/2304*x^2-819/256*x;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function v=partf(x)

v=parte(x);

v=v^2;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Professor function rombf copied here so I do not

% have to create too many .m files

% I removed the param argument as I do not see

% why I need it.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function R = rombf(a,b,N,func)

% Function to compute integrals by Romberg algorithm

% R = rombf(a,b,N,func)

% Inputs

% a,b Lower and upper bound of the integral

% N Romberg table is N by N

% func Name of integrand function in a string such as

% func='errintg'. The calling sequence is func(x,param)

% Output

% R Romberg table; Entry R(N,N) is best estimate of

% the value of the integral

%* Compute the first term R(1,1)

h = b - a; % This is the coarsest panel size

np = 1; % Current number of panels

R(1,1) = h/2 * (feval(func,a) + feval(func,b));

%* Loop over the desired number of rows, i = 2,...,N

for i=2:N

%* Compute the summation in the recursive trapezoidal rule

h = h/2; % Use panels half the previous size

np = 2*np; % Use twice as many panels

sumT = 0;

for k=1:2:np-1 % This for loop goes k=1,3,5,...,np-1

sumT = sumT + feval(func, a + k*h);

end

%* Compute Romberg table entries R(i,1), R(i,2), ..., R(i,i)

R(i,1) = 1/2 * R(i-1,1) + h * sumT;

m = 1;

for j=2:i

m = 4*m;

R(i,j) = R(i,j-1) + (R(i,j-1) - R(i-1,j-1))/(m-1);

end

end

return;