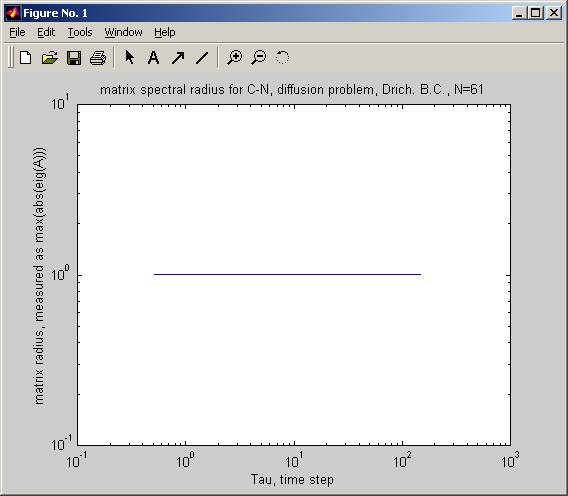
Problem 9.13 part b

Run this for C-N from tau=0.01 to tau 100.

At each time step, found matrix radius with the help of matlab max(abs(eig(B))).

Found that matrix radius is always 1 for every time step value.

This shows that N-C is matix stable for all tau.

» nma_problem_9_13_part_b

program to solve problem 9.13 part b

Nasser Abbasi

Enter N, number of grid points (suggest 61):61

Warning: Requested axes limit range too small; rendering with minimum range allowed by machine precision.

> In D:\nabbasi\data\nabbasi_web_page\academic\my_courses\phys_240\HW24\nma_problem_9_13_part_b.m at line 31

»

code:

function nma_problem_9_13_part_b()

%

%program to solve problem 9.13 part b

%Nasser Abbasi

clear all; help nma_problem_9_13_part_b;

N=input('Enter N, number of grid points (suggest 61):');

I = eye(N);

D = makeD(N);

L = 1;

kappa = 1; % diffusion coeff.

h = L/(N-2); % periodic

tsigma = h^2/(2*kappa);

i = 0;

tau = 0.01;

tauIncr = 0.5;

for(nstep = 1:300)

tau = tau+tauIncr;

coeff2 = tau/(4*tsigma); % for C-N

B = inv(I - (coeff2*D)) * (I + (coeff2*D));

i = i+1;

time(i) = tau;

radius(i) = max(abs(eig(B)));

end

loglog(time,radius);

set(gca,'Ylim',[1e-1 1e1]);

title('matrix spectral radius for C-N, diffusion problem, Drich. B.C., N=61');

xlabel('Tau, time step');

ylabel('matrix radius, measured as max(abs(eig(A)))');

%%%%%%%%%%%%%%%%%%%%%%%%%

% makes the D matrix for the

% periodic B.C.

%%%%%%%%%%%%%%%%%%%%%%%%%

function D=makeD(N)

D=zeros(N);

for(i=2:N-1)

for(j=1:N)

if( j == i+1)

D(i,j) = 1;

end

if( j == i-1)

D(i,j) = -1;

end

end

end

% now do the first and last rows

D(1,2) = 1;

D(1,N) = -1;

D(N,1) = 1;

D(N,N-1) = -1;