Problem 11.4

Nasser Abbasi

To solve this I need to integrate this below for a number of velocities.

I used the function rombf.m by Dr Garica to do the actual romberg integration. I pass it ‘func’ I wrote to evaluate the integrand each time it is called.

I found I need to know the mass m of N2,To find mass of Nitrogen particle, I looked up the periodic table and found atomic mass of N is 14.00674 grams per mole. Since we have 2 N atoms to make up one Nitrogen molecule, then the mass of N2 = 28.01348 grams per mole.

Since a mole has 6.02x10^23 molecules, then one N2 molecule has mass of 28.01348/6.02e+23 grams. Since a Kg = 1000 grams, then one N2 molecule has mass of 28.01348/(6.02e+26) kg. This is what I’ll use for m in the following equation.

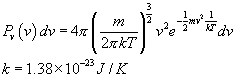
main difficulty I had with this problem is to generate the average speed <v> plot as in the answer in the back. I am getting <v> below the 0.01 probability which does not make sense. I used equation 11.10 to find <v> while for the others I used romberg integration for 11.9 equation . I am not able so far to find why <v> is coming below the other plots.

>problem_11_4

solves problem 9.4

Nasser Abbasi

code:

function problem_11_4()

%

% solves problem 9.4

% Nasser Abbasi

clear all; help problem_11_4;

probabilityValues=[0.01 0.5 0.99];

tickSym=['o' '.' '+' '-'];

figure;

for(i=1:length(probabilityValues))

result=process(probabilityValues(i))

loglog(result(:,1),result(:,2),tickSym(i));

drawnow;

hold on;

end

% now plot the <v> on the same graph

i=0;

mass=4.6534e-026; % mass on N2 in KG

k=1.38e-23;

result=[];

for(T=1:100:3000)

i=i+1;

result(i,1)=T;

speed=2*sqrt(2/pi)*sqrt(k*T/mass);

result(i,2)=speed;

end

loglog(result(:,1),result(:,2),tickSym(4));

legend('0.01','0.5','0.99','<v>');

title('velosity probability vs. Temperature for N2');

xlabel('Temperature (K)');

ylabel('Velosity (m/s)');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% do Romberg integration.

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function result=process(a)

func='problem_11_4_integrand'; % called by rombf.m

N=5;

i=0;

for(T=1:100:3000)

more=1;

speed=0;

while(more)

speed=speed+100;

% find the probablity that the particle has

% v less than current speed variable.

R=rombf(0,speed/1000,N,func,T);

if(R(N,N) >= a )

more=0;

end

end

i=i+1;

result(i,1)=T;

result(i,2)=speed;

% fprintf('speed=%d,T=%d\n',speed,T);

end

function f=problem_11_4_integrand(speed,T)

%

%Integrand for problem_11_9 to be called by rmobf.m

%Nasser Abbasi

%mass = 28.01348/(6.02e+26);

mass=4.6534e-026;

k=1.38e-23;

%mass = 2.56868181818182e-020;

f = 4 * pi * (mass/(2*pi*k*T));

f = f^(3/2);

f = f * speed^2;

f = f * exp(-(0.5*mass*speed^2)/(k*T));

%speedOfSound=0.331; % speed of sound .33 Km/sec

%mass_over_K_T=(5/3)/(speedOfSound^2);

%f=4*pi*(mass_over_K_T* 1/(2*pi));

%f = 4 * pi * (mass/(2*pi*k*T));

%f=f^(3/2);

%f=f*(speed^2);

%f=f*exp(-(3/2));