HW 4, 2.2

By Nasser Abbasi

First part, write a program that computers f’(x) using equation f’(x) = [f(x+h)-f(x)] / h and plot a graph of absolute error similar to figure 1.3.

Source code

function nma_HW2_2_error

%function nma_HW2_2_error

%

% Illustrates the error in the calculation of f'(x)= [f(x+delta)-f(x)]/delta

% as delta changes (becomes smaller and smaller).

%

% This is the solution to problem 2.2, first part.

%

%

% We look only at the error using f(x)=x^2. where f'(x)= 2x, and

% evaluate the derivative at x=1.

%

%HW 4, 2.2

%Nasser Abbasi, phy 240, Sam Jose State Univ.

%Feb 6, 2002

% struct to hold the data as we iterate

struct err { ...

value : 0 ...

delta : 0 };

x=1; % some x value to compare the error at.

DERIVE_EXACT = 2; % since f'(x) is 2x, at x=1 is 2;

delta =1;

for i=1:21

deriveApprox = ( f(x+delta) - f(x) ) / delta;

err.value(i) = abs(DERIVE_EXACT - deriveApprox);

err.delta(i) = delta;

delta = delta/10;

end

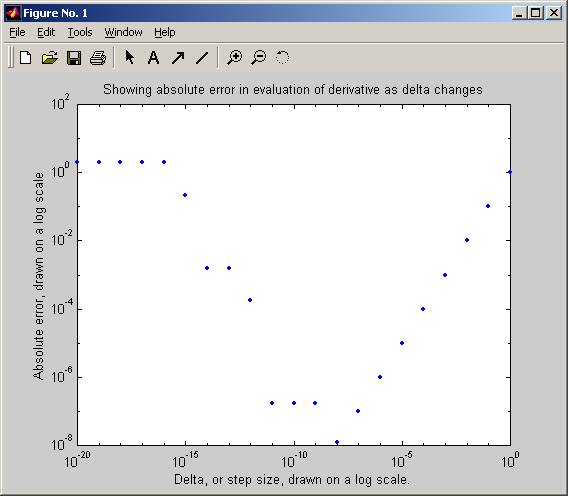
loglog(err.delta,err.value,'.');

title('Showing absolute error in evaluation of derivative as delta changes');

xlabel('Delta, or step size, drawn on a log scale.');

ylabel('Absolute error, drawn on a log scale');

% this legened below will not fit well on the diagram, need

% to figure how to do this better later.

%legend('abs err=| df(x)/dx-[f(x+delta)-f(x)]/delta',0);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% The function that we are finding its

% derivative.

%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [y]=f(x)

y=x*x;

OUTPUT

» clear all;

» help nma_HW2_2_error

function nma_HW2_2_error

Illustrates the error in the calculation of f'(x)= [f(x+delta)-f(x)]/delta

as delta changes (becomes smaller and smaller).

This is the solution to problem 2.2, first part.

We look only at the error using f(x)=x^2. where f'(x)= 2x, and

evaluate the derivative at x=1.

» nma_HW2_2_error