Problem 2.5
By Nasser Abbasi, Feb 9, 2002.
SOURCE code
%
nma_balle_HW_2_5 - Program to compute the trajectory of a baseball
% using
the Euler method.
%HW 5,
2.5, Nasser Abbasi, feb 9, 2002.
%Modified
from original teacher program balle.m
%
%This
program determines the horizental and vertical (extra, not
%requested
in HW) range as a function of the initial angle, for
%fixed
initial speed (50 m/s) and initial hight (1 m)
%
%It
plots 2 figures, one for the X range, and one for the Y range,
%and on
each plots it shows the range for the condition of no Air
%resistance,
and Air resistance. (of course, with no
Air
%resistance,
larger ranges are expected.)
clear; help nma_balle_HW_2_5; % Clear
memory and print header
% Where
we store data during simulation
data = struct ( 'angleInDegree' , 0, ...
'maxXRangeNoAir' ,
0, ...
'maxXRange' , 0, ...
'maxYRnageNoAir' ,
0, ...
'maxYRange' , 0);
%* Set
initial position and velocity of the baseball
initialY = 1; % in meter
initialX = 0;
initialPos = [initialX, initialY];
initialSpeed = 50; %
Initial speed in m/s
initialAngle = 10; %
Initial angle in degrees
finalAngle = 50;
% in degrees
%* Set
physical parameters (mass, Cd, etc.)
Cd = 0.35;
% Drag coefficient (dimensionless)
area = 4.3e-3;
% Cross-sectional area of projectile
(m^2)
g = 9.81; % Gravitational acceleration
(m/s^2)
mass = 0.145;
% Mass of projectile (kg
rho = 1.2;
% Density of air (kg/m^3
airConst =
-0.5*Cd*rho*area/mass; % Air resistance constant
tau = input('Enter
timestep, tau (sec): '); % (sec)
% to
record outer step number, independent on angle granuality
N=0;
for angle=
initialAngle:finalAngle
N=N+1;
% Initialize the initial
velosity and speed
initialVelosity =
[initialSpeed*cos(angle*pi/180), ...
initialSpeed*sin(angle*pi/180)];
% we track both pos and Vel for
no Air and Air cases during same run.
% Set initial position and
velocity for both conditions.
currentPos =
initialPos;
currentVelosity =
initialVelosity;
currentPosNoAir =
initialPos;
currentVelosityNoAir = initialVelosity;
% to track the Y max per run.
Extra, no required by HW.
maxYNoAir = currentPosNoAir(2);
maxY =
currentPos(2);
istep=0;
% keep running untill the ball
hits the ground. Note: we track both
% with Air and No Air during
the same loop, so keep running even if one
% ball has hit the ground, but
the other still falling. faster
% than having one loop per
each. do both in the same loop.
while( currentPos(2) > 0 |
currentPosNoAir(2) > 0 )
istep = istep+1;
t =
(istep-1)*tau; % Current time
if( currentPosNoAir(2) >
0 )
currentPosNoAir(1) = initialPos(1) +
initialVelosity(1)*t;
currentPosNoAir(2) = initialPos(2) +
initialVelosity(2)*t - 0.5*g*t^2;
if( currentPosNoAir(2)
> maxYNoAir )
maxYNoAir = currentPosNoAir(2);
end
end
if( currentPos(2) > 0 )
%* Calculate the
acceleration of the ball
accel =
airConst*norm(currentVelosity)* currentVelosity; %
Air resistance
accel(2) = accel(2)-g; %
Gravity
%* Calculate the new
position and velocity using Euler method
currentPos
= currentPos + tau*currentVelosity;
% Euler step
currentVelosity = currentVelosity + tau*accel;
if( currentPos(2) >
maxY )
maxY = currentPos(2);
end
end
end
% both balls have hit the
ground. record where, to plot later.
data.angleInDegree(N)
= angle;
data.maxXRange(N)
= currentPos(1);
data.maxXRangeNoAir(N) = currentPosNoAir(1);
data.maxYRange(N)
= maxY;
data.maxYRangeNoAir(N) = maxYNoAir;
end
% plot results
[K,I]=max(data.maxXRangeNoAir);
fprintf('Max horizental range (No Air)=%g meter at angle=%d\n',K,data.angleInDegree(I));
[K,I]=max(data.maxXRange);
fprintf('Max horizental range =%g meter at angle=%d\n',K,data.angleInDegree(I));
[K,I]=max(data.maxYRangeNoAir);
fprintf('Max vetical range (No Air)=%g meter at angle=%d\n',K,data.angleInDegree(I));
[K,I]=max(data.maxYRange);
fprintf('Max vertical range =%g meter at angle=%d\n',K,data.angleInDegree(I));
%* Graph
Range vs Angle
clf; figure(gcf); % Clear figure window and bring
it forward
plot(data.maxXRange,
data.angleInDegree,'+');
hold on;
plot(data.maxXRangeNoAir,
data.angleInDegree,'-');
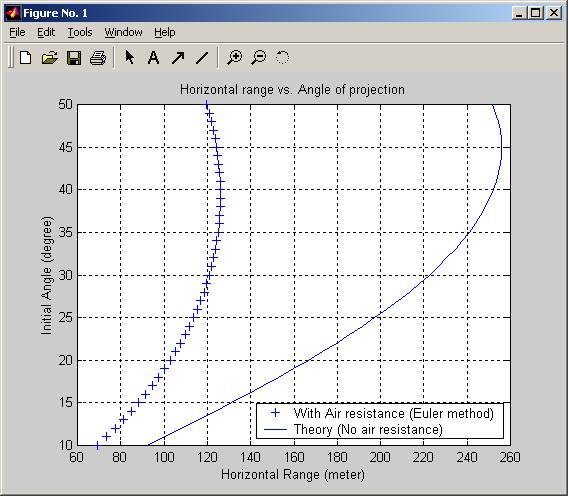
legend('With Air resistance (Euler method)','Theory (No air resistance)',4);
xlabel('Horizontal Range (meter)'); ylabel('Initial
Angle (degree)');
title('Horizontal range vs. Angle of projection');
grid on;
figure;
plot(data.maxYRange,
data.angleInDegree,'+');
hold on;
plot(data.maxYRangeNoAir,
data.angleInDegree,'-');
legend('With Air resistance (Euler method)','Theory (No air resistance)',4);
xlabel('Vertical Range (meter)'); ylabel('Initial
Angle (degree)');
title('Vertical range vs. Angle of projection');
grid on;
RESULTS
»
close all
»
clear all
»
help nma_balle_HW_2_5
nma_balle_HW_2_5 - Program to compute the
trajectory of a baseball
using the Euler method.
»
nma_balle_HW_2_5
nma_balle_HW_2_5 - Program to compute the
trajectory of a baseball
using the Euler method.
Enter
timestep, tau (sec): 0.001
Max
horizental range (No Air)=255.867 meter at angle=45
Max horizental range =126.012 meter at angle=39
Max
vetical range (No Air)=75.7737 meter at angle=50
Max
vertical range =48.1907 meter at angle=50