HW 2

HW 2.21

By Nasser Abbasi

SOURCE CODE

function nma_pendul

% nma_pendul - Program to determine effect of pivot driving

% accelration on the oscillation of the pendulum.

% Nasser Abbasi, HW 6, problem 2.22

% Modified from the original pendul.m program by Dr Garcia.

clear all; help nma_pendul % Clear the memory and print header

%* Set initial position and velocity of pendulum

theta0 = input('Enter initial angle (in degrees): ');

theta = theta0*pi/180; % Convert angle to radians

tau = input('Enter time step: ');

Td = input('Enter Td, the driving period (sec):');

initial_A= input('Enter the initial A to use (multiples of g):');

last_A = input('Enter the maximum A to use (multiples of g):');

%* Loop over desired number of steps with given time step

nstep = input('Enter number of time steps: ');

% Run the simulation for different A, the amplitude of the

% driving accelaration, and plot the result for each run to

% see the effect of increasing A on the oscillation of the

% pendulum.

for(A= initial_A : 5 : last_A)

simulate(A,theta,tau,Td,nstep);

end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Function to run the simulation for different

% values of A, with everything else fixed to see

% the effect of changing A.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function simulate(A,theta,tau,Td,nstep)

omega = 0; % Set the initial velocity

%* Set the physical constants and other variables

time = 0; % Initial time

irev = 0; % Used to count number of reversals

%* Take one backward step to start Verlet

accel = - getAccelaration( time, A, Td, theta); % Gravitational accel

theta_old = theta - omega*tau + 0.5*tau^2*accel;

for istep=1:nstep

%* Record angle and time for plotting

t_plot(istep) = time;

th_plot(istep) = theta*180/pi; % Convert angle to degrees

time = time + tau;

%* Compute new position and velocity using Verlet method

accel = - getAccelaration( time, A, Td, theta);

theta_new = 2*theta - theta_old + tau^2*accel;

theta_old = theta;

theta = theta_new;

end

%* Graph the oscillations as theta versus time

figure;

plot(t_plot,th_plot,'+');

xlabel('Time'); ylabel('\theta (degrees)');

title(sprintf('Oscillation for initial angle=%d (degree), A0=%d', ...

th_plot(1), A));

drawnow;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% function to find the accelatation from

% 2*PI*time

% g (1 + A Sin(------------) )

% Td

% ------------------------------ Sin (theta)

% L

%%%%%%%%%%%%%%%%%%%%%%%%%%

function w=getAccelaration(time,A,Td,theta)

% notice, g/L is taken as 1

w= 1 + A*sin(2*pi*time/Td) ;

w= w * sin(theta);

Analysis

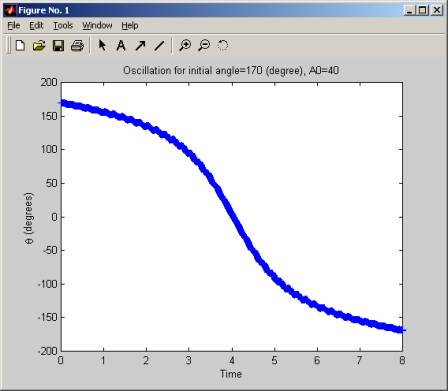
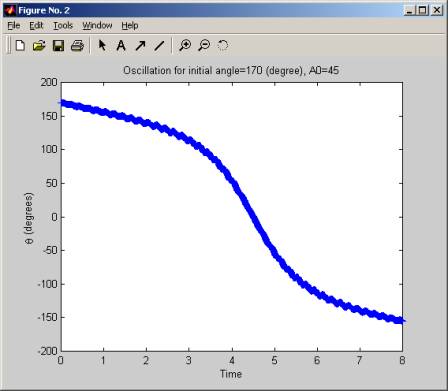
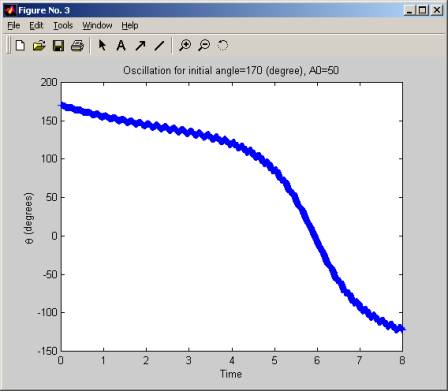
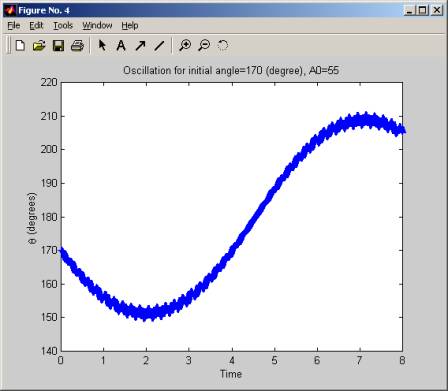
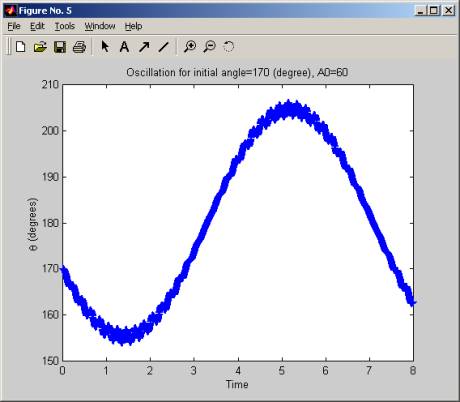
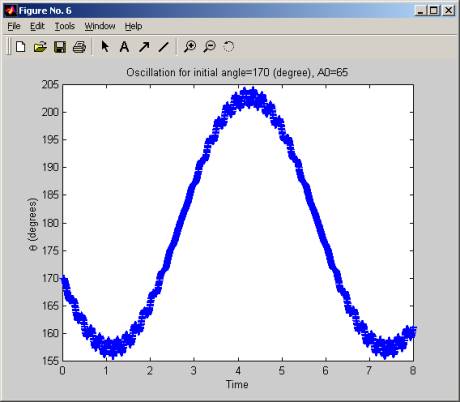
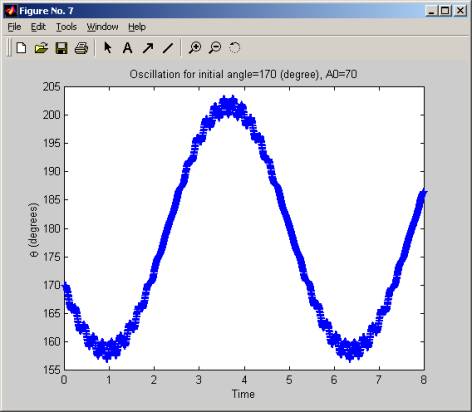
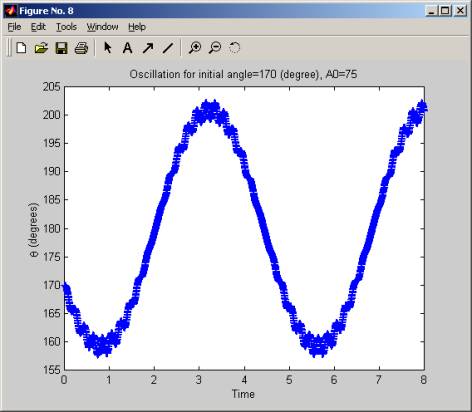
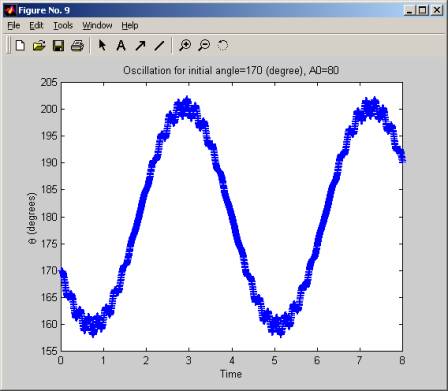
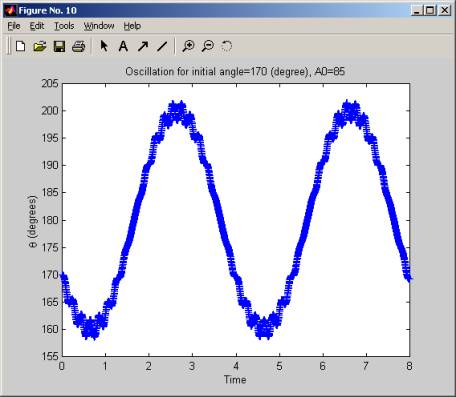
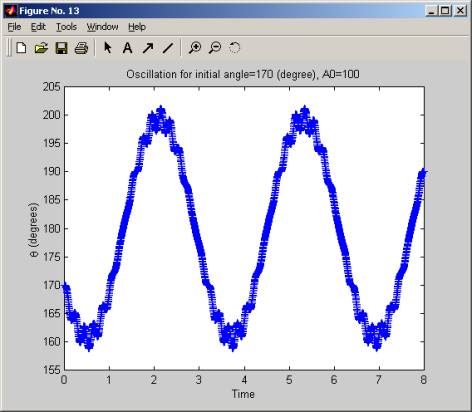
The simulation was started with a large fixed initial angle (170 degrees), then A, the amplitude of the acceleration of the pivot holding the pendulum was increased slowly, (in increment of 5 g), and for each value of A, we plot the oscillation of the pendulum. We see that for low values of A, the pendulum is not stable, but when A crosses over the value of 55g to 60g the pendulum start to oscillate around the initial angle. As A is increased more, this oscillation become more frequent and at A of 100g, the pendulum makes a little over 2 full swings in 8 seconds. The range of the oscillation (the angle over which it swings remains the same, which is from about 160 degrees to 200 degrees, but the frequency increases as A increases.