HW 3.5

Nasser Abbasi

SOURCE CODE

% nma_orbit - Program to compute the orbit of a comet.

clear all; help nma_orbit; % Clear memory and print header

%

% Nasser Abbasi, HW 3.5. Modified from teacher orbit.m

%

% Add Verlet method

%

% r_next - r_before

% v_now = ---------------------

% 2 TAO

%

%

% r_next = 2 r_now - r_before + TAO^2 * accel_now

%

%

% The initial r entered is r_now, so we need to find r_before

% i.e. r_0. To do that, use this:

%

% TAO^2

% r_before = r_now - TAO v_now + ------- accel_now

% 2

%

%* Set initial position and velocity of the comet.

r0 = input('Enter initial radial distance (AU): ');

v0 = input('Enter initial tangential velocity (AU/yr): ');

r_now = [r0 0];

v_now = [0 v0];

state = [ r_now(1) r_now(2) v_now(1) v_now(2) ]; % Used by R-K routines

%* Set physical parameters (mass, G*M)

GM = 4*pi^2; % Grav. const. * Mass of Sun (au^3/yr^2)

mass = 1.; % Mass of comet

adaptErr = 1.e-3; % Error parameter used by adaptive Runge-Kutta

time = 0;

%* Loop over desired number of steps using specified

% numerical method.

nStep = input('Enter number of steps: ');

tau = input('Enter time step (yr): ');

%

% menu keeps hanging my Matlab 5.3.1 on win2k, so I am using this

% way to input the method to use

%

numericalMethod= input('choose a numerical method: 1=Euler, 2=Euler-Cromer, 3=RK, 4=Adaptive-RK, 5=Verlet:');

if( numericalMethod == 5 ) %verlet, find the r_before to kick off the simulation

accel_now = -GM*r_now/norm(r_now)^3;

r_before = r_now - tau*v_now + (0.5*tau^2)* accel_now;

end

for iStep=1:nStep

%* Record position and energy for plotting.

rplot(iStep) = norm(r_now); % Record position for polar plot

thplot(iStep) = atan2(r_now(2),r_now(1));

tplot(iStep) = time;

kinetic(iStep) = .5*mass*norm(v_now)^2; % Record energies

potential(iStep) = - GM*mass/norm(r_now);

%* Calculate new position and velocity using desired method.

switch numericalMethod

case 1

accel_now = -GM*r_now/norm(r_now)^3;

r_next = r_now + tau*v_now; % Euler step

v_next = v_now + tau*accel_now;

time = time + tau;

r_now = r_next;

v_now = v_next;

case 2

accel_now = -GM*r_now/norm(r_now)^3;

v_next = v_now + tau*accel_now;

r_next = r_now + tau*v_next; % Euler-Cromer step

time = time + tau;

r_now = r_next;

v_now = v_next;

case 3

state = rk4(state,time,tau,'gravrk',GM);

r_now = [state(1) state(2)]; % 4th order Runge-Kutta

v_now = [state(3) state(4)];

time = time + tau;

case 4

[state time tau] = rka(state,time,tau,adaptErr,'gravrk',GM);

r_now = [state(1) state(2)]; % Adaptive Runge-Kutta

v_now = [state(3) state(4)];

case 5

% verlet method

accel_now = -GM*r_now/norm(r_now)^3;

r_next = 2*r_now - r_before + (tau^2 * accel_now);

v_now = (r_next - r_before)/(2*tau);

time = time + tau;

r_before = r_now;

r_now = r_next;

end

end

%* Graph the trajectory of the comet.

figure(1); clf; % Clear figure 1 window and bring forward

polar(thplot,rplot,'+'); % Use polar plot for graphing orbit

xlabel('Distance (AU)'); grid;

S=sprintf('Initial radial dist=%g (AU), Initial V=%g (AU/yr), tau=%g (AU yr), nStep=%d',r0,v0,tau,nStep);

title(S);

pause(1) % Pause for 1 second before drawing next plot

%* Graph the energy of the comet versus time.

figure(2); clf; % Clear figure 2 window and bring forward

totalE = kinetic + potential; % Total energy

plot(tplot,kinetic,'-.',tplot,potential,'--',tplot,totalE,'-')

legend('Kinetic','Potential','Total');

xlabel('Time (yr)'); ylabel('Energy (M AU^2/yr^2)');

OUTPUT

» nma_orbit

nma_orbit - Program to compute the orbit of a comet.

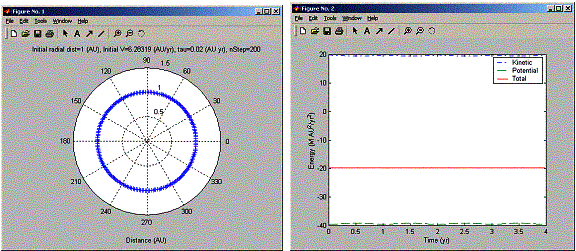
Enter initial radial distance (AU): 1

Enter initial tangential velocity (AU/yr): 2*pi

Enter number of steps: 200

Enter time step (yr): 0.02

choose a numerical method: 1=Euler, 2=Euler-Cromer, 3=RK, 4=Adaptive-RK, 5=Verlet:5

»

» clear all

» nma_orbit

nma_orbit - Program to compute the orbit of a comet.

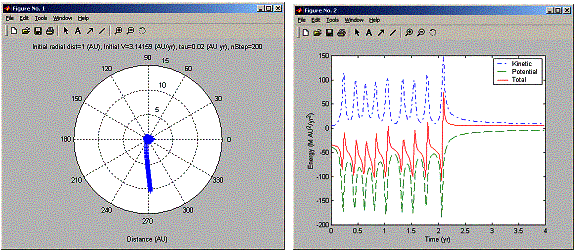
Enter initial radial distance (AU): 1

Enter initial tangential velocity (AU/yr): pi

Enter number of steps: 200

Enter time step (yr): 0.02

choose a numerical method: 1=Euler, 2=Euler-Cromer, 3=RK, 4=Adaptive-RK, 5=Verlet:5

»

» clear all

» nma_orbit

nma_orbit - Program to compute the orbit of a comet.

Enter initial radial distance (AU): 1

Enter initial tangential velocity (AU/yr): pi

Enter number of steps: 200

Enter time step (yr): 0.005

choose a numerical method: 1=Euler, 2=Euler-Cromer, 3=RK, 4=Adaptive-RK, 5=Verlet:5

»