Project one. Problem one. Mathematics 502 Probability and Statistics

Nasser Abbasi, September 26,2007. California State University, Fullerton

Problem 1 part (a)

The CDF given is defined as   To find we need to solve for x in the equation for x≥0 Hence we write

-λx=ln(1-y)

Therefore

Now to generate random numbers which belongs to an exponential distribution, we will now generate random numbers from U(0,1) and for each such number generated, we will apply the above function on it, and the result will be a random number which belongs to the exponential distribution.  For example, if λ=2 and a uniform random number is say 0.4, then we evaluate
And so this is the idea to implement. We need to first seed the uniform random number generator before we start.

Algorithm

Input: λ: parameter, n: number of random numbers to generate
output: a list of n random numbers from the probability density function ~ F(x) given above.

1. Seed the uniform random number generator with (010101).
2. initialize the array d of size n which will contain the list of random numbers generated below.

This loop below is just an algorithmic view. In actual code, a 'vector' operation Table[] in used for speed.
3. For i in 1..n LOOP
       Generate which is a random generated from uniform distribution using the build in function RandomReal[0,1]
        d[i]= using input λ.
    END LOOP

4. Find histogram of d. Select an appropriate number of bins. Let be the histogram found.
5. Now find the relative frequency by dividing set by the number of observations n. Hence histogram now is
6. Now scale the histogram such that it is density. Total area is 1. Do this by finding total area under histogram, and divide each bin count by this area.
7. Plot the histogram and the exponential distribution  λ on the same plot.

Code Implementation

Define the function which was derived earlier. This is the inverse of the CDF of the exponential density function

Problem 1 part(b)

Generate n = 10000 for λ = 2 and overlay with relative frequency, use appropriate number of bins. See appendix for the function postProcessForPartOne[] which generate the plots. Removed below to reduce code clutter in the main report.

This function makes a histogram which is scaled to be used to overlay density plots, or other functions.
Input:  originalData: this is an array of numbers which represents the data to bin
          nBins: number of bins
output: the histogram itself but scaled such that area is ONE

This function to overlay the histogram and the PDF. It is used by the simulation program as well (that is why it is a little larger than needed)

now generate the needed outout for N = 10000

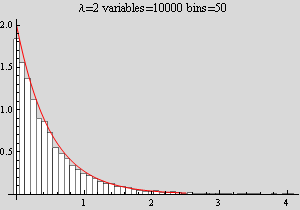Comment and analysis

Below I show snap shots of few plots of the density overlaid with the histogram for different values of n which is the number of random variables.

We see from the plots below, that for a fixed number of bins, fixed λ, that as more random variables are generated, the histogram overlaid on top of the actual PDF becomes closer and closer to the PDF curve. The error between the histogram and the PDF curve becomes smaller the larger the number of random variables used. This indicates that this method of finding random numbers for density function will converge to the density function. We need to select an appropriate bin size to see this more clearly. The smaller the bin size the more clear this will become (but too small a bin size will make the histogram itself not too clear).

Please see appendix for additional GUI based simulation for this part of the project.

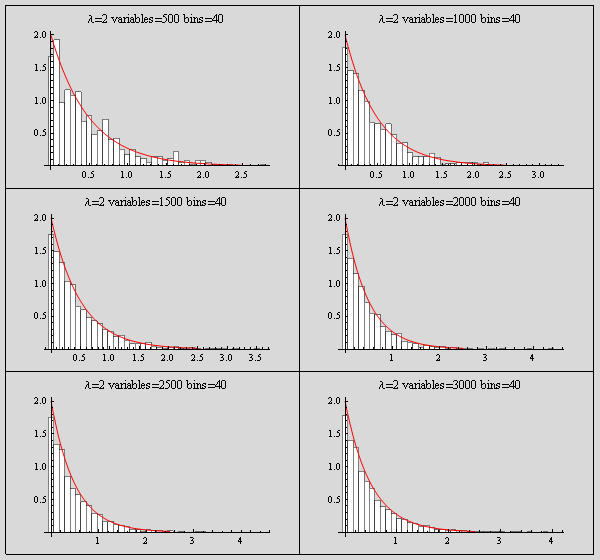
Problem 1 simulation

Define function which accepts a list of random variables from exponential distribution, and λ and generates a plot of the histogram overlaid by the exponential density plot.

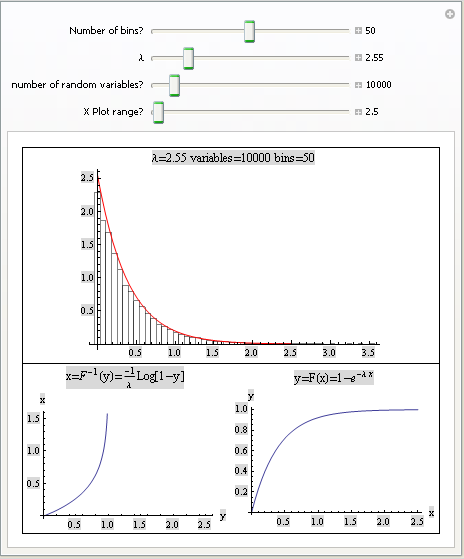
Created by Wolfram Mathematica 6.0 for Students - Personal Use Only  (25 September 2007)