problem: If B is similar to A and C is similar to B, show that C is similar to A. What matrices are similar to \(I\)?
answer:
Since B is similar to A and C is similar to B, then we have the following
\begin{align} S_{1}^{-1}CS_{1} & =B\ \tag{1}\\ S_{2}^{-1}BS_{2} & =A\ \tag{2} \end{align}
From (1) and (2)\begin{align*} S_{2}^{-1}BS_{2} & =A\\ S_{2}^{-1}\left ( S_{1}^{-1}CS_{1}\right ) S_{2} & =A\\ \left ( S_{2}^{-1}S_{1}^{-1}\right ) C\left ( S_{1}S_{2}\right ) & =A\\ \left ( S_{1}S_{2}\right ) ^{-1}C\left ( S_{1}S_{2}\right ) & =A \end{align*}
Let \(S_{1}S_{2}=S_{3}\), hence the above becomes\[ S_{3}^{-1}CS_{3}=A \] Hence \(C\) is similar to \(A.\) Now for the second part. We write\begin{align*} S^{-1}AS & =I\\ S^{-1}A & =S \end{align*}
So \(A\) must be \(I\), hence only \(I\) is similar to \(I.\)
problem: Describe in words all the matrices that are similar to \(\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \), and find 2 of them
answer:
Let \(A\) be the above matrix. The above matrix represents a reflection across the x-axis. Hence Reflection across the y axis will be similar to it. Any multiple of this reflection matrix will also be similar to \(A.\)
Since reflection across the y-axis is \(B=\) \(\begin{pmatrix} -1 & 0\\ 0 & 1 \end{pmatrix} \) then this \(B\) matrix is similar to \(A\)
Then any multiple of \(B\) is also similar to \(A\), such as \(\begin{pmatrix} -10 & 0\\ 0 & 10 \end{pmatrix} \) and \(\begin{pmatrix} -20 & 0\\ 0 & 20 \end{pmatrix} \)
Problem: show (if \(B\) is invertible) then \(BA\) is similar to \(AB\)
answer: we want to show that \(M^{-1}\left ( BA\right ) M=AB\)
Let \(M^{-1}\left ( BA\right ) M=H\,\), i.e. let \(BA\symbol{126}H\), and try to show that \(H=AB\)
\begin{align*} M^{-1}\left ( BA\right ) M & =H\\ \left ( BA\right ) M & =MH\\ BA & =MHM^{-1}\\ A & =B^{-1}MHM^{-1}\\ AB & =B^{-1}MHM^{-1}B\\ AB & =\left ( B^{-1}M\right ) H\left ( M^{-1}B\right ) \\ AB & =\left ( M^{-1}B\right ) ^{-1}H\left ( M^{-1}B\right ) \end{align*}
Let \(M^{-1}B=Z\), hence the above becomes
\[ AB=Z^{-1}HZ \]
Then \(H\symbol{126}AB\)
But we started by stating that \(H\symbol{126}BA\), and since if \(r_{1}\symbol{126}r_{2}\) and \(r_{2}\symbol{126}r_{3}\) then \(r_{1}\symbol{126}r_{3}\) then we showed \(BA\symbol{126}AB.\)
problem: find normal matrix (\(NN^{H}=N^{H}N)\) that is not Hermitian, skew symmetric, unitary, or diagonal. Show that all permutation matrices are normal
answer:
problem: quadratic \(f=x^{2}+4xy+2y^{2}\) has saddle point at origin, despite that its coefficients are positive. Write \(f\) as difference of 2 squares
answer: Let \(f=\left ( ax+by\right ) ^{2}-\left ( cx+dy\right ) ^{2}\), hence
\begin{align*} f & =\left ( ax+by\right ) ^{2}-\left ( cx+dy\right ) ^{2}\\ & =a^{2}x^{2}+b^{2}y^{2}+2abxy-\left ( c^{2}x^{2}+d^{2}y^{2}+2cdxy\right ) \\ & =a^{2}x^{2}+b^{2}y^{2}+2abxy-c^{2}x^{2}-d^{2}y^{2}-2cdxy\\ & =x^{2}\left ( a^{2}-c^{2}\right ) +y^{2}\left ( b^{2}-d^{2}\right ) +xy\left ( 2ab-2cd\right ) \end{align*}
Hence, compare coefficients, we have \(a^{2}-c^{2}=1,b^{2}-d^{2}=2,2ab-2cd=4\)
so \(ab-cd=2.\)
Let \(c=1,\) then we have
\(a^{2}=2\) ,\(b^{2}-d^{2}=2,2ab-2d=4\)
3 equations in 3 unknown. Solve with computer for speed (running out of time!) I get one of the solutions as
\(d=0,a=-\sqrt{2},b=-\sqrt{2}\)
So \(f=\left ( ax+by\right ) ^{2}-\left ( cx+dy\right ) ^{2}=\)\(\left ( -\sqrt{2}x+-\sqrt{2}y\right ) ^{2}-\left ( x\right ) ^{2}\)
problem: decide for or against PD for these matrices, write out corresponding \(f=x^{T}Ax\)
Answer: I use \(a>0\), and \(ac>b^{2}\) test where \(A=\begin{pmatrix} a & b\\ b & c \end{pmatrix} \)
\(\begin{pmatrix} 1 & 3\\ 3 & 5 \end{pmatrix} \rightarrow 1>0,5>9\) no, Not PD \(\rightarrow f=ax^{2}=2bxy+cy^{2}\rightarrow \)\(f=x^{2}+6xy+3y\)
\(\begin{pmatrix} 1 & -1\\ -1 & 1 \end{pmatrix} \rightarrow a>0,1>1,\)no, Not PD \(\rightarrow f=ax^{2}=2bxy+cy^{2}\rightarrow \)\(f=x^{2}-2xy+y\)
\(\begin{pmatrix} 2 & 3\\ 3 & 5 \end{pmatrix} \rightarrow a>0,10>9,\)yes, PD \(\rightarrow f=ax^{2}=2bxy+cy^{2}\rightarrow \)\(f=2x^{2}+6xy+5y\)
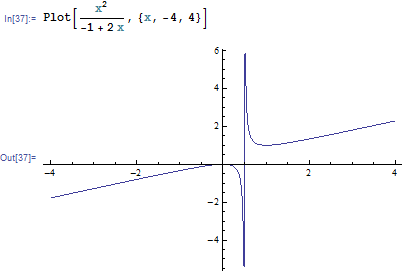
\(\begin{pmatrix} -1 & 2\\ 2 & -8 \end{pmatrix} \rightarrow -1>0,no\) Not PD \(\rightarrow f=ax^{2}+2bxy+cy^{2}\rightarrow \)\(f=-x^{2}+4xy-8y\)
For (b) we have \(f=x^{2}-2xy+y\), if \(y=\frac{x^{2}}{2x-1}\) then \(f=x^{2}-2x\frac{x^{2}}{2x-1}+\frac{x^{2}}{2x-1}=\allowbreak 0\), hence I plot this:

And along the lines shown is \(f=0\)
problem: if A is 2x2 symmetric matrix, passes test that a\(>\)0 , \(ac>b^{2}\) solve equation \(\det \left ( A-\lambda I\right ) =0\) and show that eigenvalues are \(>\)0
answer:
Matrix is PD, then \begin{align*} det\left ( \begin{pmatrix} a & b\\ b & c \end{pmatrix} -\lambda \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} \right ) & =0\\ \left \vert \begin{pmatrix} a-\lambda & b\\ b & c-\lambda \end{pmatrix} \right \vert & =0\\ \left ( a-\lambda \right ) \left ( c-\lambda \right ) -b^{2} & =0\\ ac-a\lambda -c\lambda +\lambda ^{2} & =0\\ \lambda ^{2}+\lambda \left ( -a-c\right ) +ac & =0 \end{align*}
Hence \(\lambda _{1}=a,\lambda _{2}=c\)
But \(a>0\,,\) so \(\lambda _{1}>0\), and given \(ac>\) positive quantity \(b^{2}\), then \(\lambda _{2}=c\rightarrow \lambda _{2}>0\)
(a) For which numbers \(b\) is \(\begin{pmatrix} 1 & b\\ b & 9 \end{pmatrix} \) PD?
\(\begin{pmatrix} a & b\\ b & c \end{pmatrix} \) is PD is \(a>0\) and \(ac>b^{2}\)
for PD need \(ac>b^{2}\), hence need \(9>b^{2}\) ie. \(b<3\) and \(b>-3\), so \(-3<b<3\)
(b)Factor \(A=LDL^{T}\) when \(b\) is in the range above
\(\begin{pmatrix} 1 & b\\ b & 9 \end{pmatrix} \rightarrow l_{21}=b\rightarrow U=\begin{pmatrix} 1 & b\\ 0 & 9-b^{2}\end{pmatrix} \)
So \(L=\begin{pmatrix} 1 & 0\\ b & 1 \end{pmatrix} ,D=\begin{pmatrix} 1 & 0\\ 0 & 9-b^{2}\end{pmatrix} ,L^{T}=\begin{pmatrix} 1 & b\\ 0 & 1 \end{pmatrix} \)
(c) What is the minimum of \(f\left ( x,y\right ) =\frac{1}{2}\left ( x^{2}+2bxy+9y^{2}\right ) -y\ \)when in this range
when \(f\left ( x,y\right ) =\frac{1}{2}\left ( x^{2}+2bxy+9y^{2}\right ) -y=\frac{1}{2}x^{2}+bxy+\frac{9}{2}y^{2}-y\)
\(\frac{\partial f}{\partial x}=x+by=0,\frac{\partial f}{\partial y}=bx+9y-1=0\)
Hence \(\begin{pmatrix} 1 & b\\ b & 9 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix} =\begin{pmatrix} 0\\ 1 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & b\\ 0 & 9-b^{2}\end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix} =\begin{pmatrix} 0\\ 1 \end{pmatrix} \)
Hence \(y=\frac{1}{9-b^{2}}\)\(,\)and \(x+by=0\rightarrow \)\(x=-\frac{b}{9-b^{2}}\)
So \(f\left ( x,y\right ) =\frac{1}{2}\left ( x^{2}+2bxy+9y^{2}\right ) -y\)
Hence \(f\left ( x,y\right ) \rightarrow \frac{1}{2}\left ( \left ( -\frac{b}{9-b^{2}}\right ) ^{2}+2b\left ( -\frac{b}{9-b^{2}}\right ) \left ( \frac{1}{9-b^{2}}\right ) +9\left ( \frac{1}{9-b^{2}}\right ) ^{2}\right ) -\left ( \frac{1}{9-b^{2}}\right ) =\allowbreak \frac{1}{2\left ( b^{2}-9\right ) }\)
So minimum is \(\allowbreak \frac{1}{2\left ( b^{2}-9\right ) }\)
(d)When \(b=3\), we see that we get \(\frac{1}{0}=\infty \) so no minimum
Problem: If \(A\) has independent columns then \(A^{T}A\) is square and symmetric and invertible. Rewrite \(\vec{x}^{T}A^{T}A\vec{x}\) to show why it is positive except when \(\vec{x}=0\), then \(A^{T}A\) is PD
answer: \(\vec{x}^{T}\left ( A^{T}A\right ) \vec{x}=\left ( A\vec{x}\right ) ^{T}A\vec{x}\)
Let \(A\vec{x}=\vec{b}\), then the above is \(\vec{b}^{T}\vec{b}=\left \Vert \vec{b}\right \Vert ^{2}\), which is positive quantity except when \(\vec{b}=\vec{0}\), which occurs when \(A\vec{x}=\vec{b}=\vec{0}\) which happens only when \(\vec{x}=\vec{0}\), since \(A\) is invertible.
Hence \(A^{T}A\) is positive definite except when \(\vec{x}=0\)
problem: If \(A=Q\Lambda Q^{T}\) is P.D. then \(R=Q\sqrt{\Lambda }Q^{T}\) is its S.P.D. square root. Why does \(R\) have positive eigenvalues? Compute \(R\) and verify \(R^{2}=A\) for \(A=\begin{pmatrix} 10 & 6\\ 6 & 10 \end{pmatrix} ,A=\begin{pmatrix} 10 & -6\\ -6 & 10 \end{pmatrix} \)
answer:
For \(A=\begin{pmatrix} 10 & 6\\ 6 & 10 \end{pmatrix} \)
Given \(R\) is P.D. (problem said so), Hence \(\vec{x}^{T}R\vec{x}>0\) for all \(\vec{x}\neq 0\)
Now (assuming in all that follows that \(x\neq 0\) \()\) \begin{align*} R\vec{x} & =\lambda \vec{x}\\ \vec{x}^{T}R\vec{x} & =x^{T}\lambda \vec{x}\\ \vec{x}^{T}R\vec{x} & =\lambda \left \Vert \vec{x}\right \Vert ^{2} \end{align*}
Since \(\vec{x}^{T}R\vec{x}>0\) then \(\lambda \left \Vert \vec{x}\right \Vert ^{2}>0\), and since \(\left \Vert \vec{x}\right \Vert ^{2}>0\) hence \(\lambda >0\)
To compute \(R\) we first need to find \(Q\).
\(A=\begin{pmatrix} 10 & 6\\ 6 & 10 \end{pmatrix} \rightarrow l_{21}=\frac{6}{10}\rightarrow \begin{pmatrix} 10 & 6\\ 6-\frac{6}{10}\times 10 & 10-\frac{6}{10}\times 6 \end{pmatrix} \rightarrow \begin{pmatrix} 10 & 6\\ 0 & \frac{32}{5}\end{pmatrix} \)
Hence \(L=\begin{pmatrix} 1 & 0\\ \frac{6}{10} & 1 \end{pmatrix} ,U=\begin{pmatrix} 10 & 6\\ 0 & \frac{32}{5}\end{pmatrix} \)
Then \begin{align*} LDU & =\begin{pmatrix} 1 & 0\\ \frac{6}{10} & 1 \end{pmatrix}\begin{pmatrix} 10 & 0\\ 0 & \frac{32}{5}\end{pmatrix}\begin{pmatrix} 1 & \frac{6}{10}\\ 0 & 1 \end{pmatrix} \\ & =\begin{pmatrix} 1 & 0\\ \frac{6}{10} & 1 \end{pmatrix}\begin{pmatrix} 10 & 0\\ 0 & \frac{32}{5}\end{pmatrix}\begin{pmatrix} 1 & 0\\ \frac{6}{10} & 1 \end{pmatrix} ^{T} \end{align*}
Hence we see that \(Q=L=\begin{pmatrix} 1 & 0\\ \frac{6}{10} & 1 \end{pmatrix} ,\Lambda =D=\begin{pmatrix} 10 & 0\\ 0 & \frac{32}{5}\end{pmatrix} ,Q^{T}=L^{T}\)
Since \(A\) is SPD, then \(A=R^{T}R\) and \(A=Q\Lambda Q^{T}\), hence we can take \(R=\sqrt{\Lambda }Q^{T}\)\begin{align*} R & =\sqrt{\Lambda }Q^{T}=\sqrt{\begin{pmatrix} 10 & 0\\ 0 & \frac{32}{5}\end{pmatrix} }\begin{pmatrix} 1 & \frac{6}{10}\\ 0 & 1 \end{pmatrix} \\ & =\begin{pmatrix} \sqrt{10} & 0\\ 0 & \sqrt{\frac{32}{5}}\end{pmatrix}\begin{pmatrix} 1 & \frac{6}{10}\\ 0 & 1 \end{pmatrix} \\ & =\begin{pmatrix} \sqrt{10} & \frac{3}{5}\sqrt{2}\sqrt{5}\\ 0 & \frac{4}{5}\sqrt{2}\sqrt{5}\end{pmatrix} \end{align*}
Verify that \(R^{T}R=A\)
\begin{align*} R^{T}R & =\begin{pmatrix} \sqrt{10} & 0\\ \frac{3}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5}\end{pmatrix}\begin{pmatrix} \sqrt{10} & \frac{3}{5}\sqrt{2}\sqrt{5}\\ 0 & \frac{4}{5}\sqrt{2}\sqrt{5}\end{pmatrix} \\ & =\begin{pmatrix} 10 & 6\\ 6 & 10 \end{pmatrix} \end{align*}
verified oK.
Now do the same for \(A=\begin{pmatrix} 10 & -6\\ -6 & 10 \end{pmatrix} \)
\(A=\begin{pmatrix} 10 & -6\\ -6 & 10 \end{pmatrix} \rightarrow l_{21}=\frac{-6}{10}\rightarrow U=\begin{pmatrix} 10 & -6\\ -6-\frac{-6}{10}\times 10 & 10-\frac{-6}{10}\times -6 \end{pmatrix} \rightarrow \begin{pmatrix} 10 & -6\\ 0 & \frac{32}{5}\end{pmatrix} \) :
Hence \(L=\begin{pmatrix} 1 & 0\\ -\frac{6}{10} & 1 \end{pmatrix} ,U=\begin{pmatrix} 10 & -6\\ 0 & \frac{32}{5}\end{pmatrix} \)
Then \begin{align*} LDU & =\begin{pmatrix} 1 & 0\\ -\frac{6}{10} & 1 \end{pmatrix}\begin{pmatrix} 10 & 0\\ 0 & \frac{32}{5}\end{pmatrix}\begin{pmatrix} 1 & -\frac{6}{10}\\ 0 & 1 \end{pmatrix} \\ & =\begin{pmatrix} 1 & 0\\ -\frac{6}{10} & 1 \end{pmatrix}\begin{pmatrix} 10 & 0\\ 0 & \frac{32}{5}\end{pmatrix}\begin{pmatrix} 1 & 0\\ -\frac{6}{10} & 1 \end{pmatrix} ^{T} \end{align*}
Hence we see that \(Q=L=\begin{pmatrix} 1 & 0\\ -\frac{6}{10} & 1 \end{pmatrix} ,\Lambda =D=\begin{pmatrix} 10 & 0\\ 0 & \frac{32}{5}\end{pmatrix} ,Q^{T}=L^{T}\)
Then now we find \(R\)
Since \(A\) is SPD, then \(A=R^{T}R\) and \(A=Q\Lambda Q^{T}\), hence we can take \(R=\sqrt{\Lambda }Q^{T}\)\begin{align*} R & =\sqrt{\Lambda }Q^{T}=\sqrt{\begin{pmatrix} 10 & 0\\ 0 & \frac{32}{5}\end{pmatrix} }\begin{pmatrix} 1 & -\frac{6}{10}\\ 0 & 1 \end{pmatrix} \\ & =\begin{pmatrix} \sqrt{10} & 0\\ 0 & \sqrt{\frac{32}{5}}\end{pmatrix}\begin{pmatrix} 1 & -\frac{6}{10}\\ 0 & 1 \end{pmatrix} \\ & =\begin{pmatrix} \sqrt{10} & -\frac{3}{5}\sqrt{2}\sqrt{5}\\ 0 & \frac{4}{5}\sqrt{2}\sqrt{5}\end{pmatrix} \end{align*}
Verify that \(R^{T}R=A\)
\begin{align*} R^{T}R & =\begin{pmatrix} \sqrt{10} & 0\\ -\frac{3}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5}\end{pmatrix}\begin{pmatrix} \sqrt{10} & -\frac{3}{5}\sqrt{2}\sqrt{5}\\ 0 & \frac{4}{5}\sqrt{2}\sqrt{5}\end{pmatrix} \\ & =\begin{pmatrix} 10 & -6\\ -6 & 10 \end{pmatrix} \end{align*}
verified oK.
Show from the eigenvalues that if A is P.D. so is \(A^{2}\) and so is \(A^{-1}\)
answer:
Given \(A\) is PD. Hence Eigenvalues of \(A\) are positive.
Let eigenvalue of \(A\) be \(\lambda _{A}\)
Let \(B=A^{2}\)
Let eigenvalue of \(B\) be \(\lambda _{B}\)
We need to show that \(\lambda _{B}>0\)
Now
\begin{align*} Bx & =\lambda _{B}x\\ A^{2}x & =\lambda _{B}x\\ AAx & =\lambda _{B}x\\ A\lambda _{A}x & =\lambda _{B}x\\ \lambda _{A}Ax & =\lambda _{B}x\\ \lambda _{A}\lambda _{A}x & =\lambda _{B}x \end{align*}
From the last statement above we can now say
\[ \lambda _{A}^{2}=\lambda _{B}\]
Hence \(\lambda _{B}>0\), hence by theorem 6B which says that if all eigenvalues are positive then the matrix is PD, then in this case the matrix \(B\) which is \(A^{2}\) is PD. QED
Now for \(A^{-1}\)
\[ Ax=\lambda _{A}x \]
pre multiply both sides by \(A^{-1}\)
\begin{align*} \overset{I}{\overbrace{A^{-1}A}}x & =A^{-1}\lambda _{A}x\\ x & =A^{-1}\lambda _{A}x\\ \frac{1}{\lambda _{A}}x & =A^{-1}x \end{align*}
i.e. \[ A^{-1}x=\frac{1}{\lambda _{A}}x \]
Hence eigenvalue of \(A^{-1}\) is \(\frac{1}{\lambda _{A}}.\) And since \(\lambda _{A}>0\), then so is \(\frac{1}{\lambda _{A}}\), and by theorem 6B again, since all eigenvalues are positive then \(A^{-1}\) is P.D.
From the pivots, eigenvalues, eigenvectors of \(A=\ \begin{pmatrix} 5 & 4\\ 4 & 5 \end{pmatrix} \), write \(A\) as \(R^{T}R\) in 3 ways
Answer:
First find if A is PD or not. Since this is a \(2\) by \(2\) matrix, a simple test is to look at the quantity \(a^{2}-bc\) and if it is positive, and if \(a\) is also positive, then the matrix is PD
\begin{align*} A & =\ \begin{pmatrix} a & b\\ c & d \end{pmatrix} \\ a & =5>0\\ a^{2}-bc & =25-16\\ & =9>0 \end{align*}
hence \(A\) is P.D.
Then it can be written as \(R^{T}R\) where \(R\) is full rank square matrix.
1) Since \(A\) is symmetric \(P.D.\), then it has choleskly decomposition \(CC^{T}\) where \(C=L\sqrt{D}\), and \(C^{T}=\sqrt{D}L^{T}\) (the pivots are positive in the \(D\) matrix diagonal, so we can take their square root)
Then we write \(A=R^{T}R=\left ( L\sqrt{D}\right ) \left ( \sqrt{D}L^{T}\right ) \) where \(R=\left ( \sqrt{D}L^{T}\right ) \)
\(\begin{pmatrix} 5 & 4\\ 4 & 5 \end{pmatrix} \rightarrow l_{21}=\frac{4}{5}\rightarrow U=\begin{pmatrix} 5 & 4\\ 0 & 5-\frac{4}{5}\times 4 \end{pmatrix} =\begin{pmatrix} 5 & 4\\ 0 & \frac{9}{5}\end{pmatrix} \)
Hence \(L=\begin{pmatrix} 1 & 0\\ \frac{4}{5} & 1 \end{pmatrix} ,U=\begin{pmatrix} 5 & 4\\ 0 & \frac{9}{5}\end{pmatrix} \rightarrow LDU=\begin{pmatrix} 1 & 0\\ \frac{4}{5} & 1 \end{pmatrix}\begin{pmatrix} 5 & 0\\ 0 & \frac{9}{5}\end{pmatrix}\begin{pmatrix} 1 & \frac{4}{5}\\ 0 & 1 \end{pmatrix} \)
Hence \(R=\sqrt{\begin{pmatrix} 5 & 0\\ 0 & \frac{9}{5}\end{pmatrix} }\begin{pmatrix} 1 & \frac{4}{5}\\ 0 & 1 \end{pmatrix} =\begin{pmatrix} \sqrt{5} & 0\\ 0 & \sqrt{\frac{9}{5}}\end{pmatrix}\begin{pmatrix} 1 & \frac{4}{5}\\ 0 & 1 \end{pmatrix} =\allowbreak \begin{pmatrix} \sqrt{5} & \frac{4}{5}\sqrt{5}\\ 0 & \frac{3}{5}\sqrt{5}\end{pmatrix} \)
Hence \[ A=\overset{L\sqrt{D}}{\overbrace{\allowbreak \begin{pmatrix} \sqrt{5} & 0\\ \frac{4}{5}\sqrt{5} & \frac{3}{5}\sqrt{5}\end{pmatrix} }\allowbreak }\overset{\sqrt{D}L^{T}}{\overbrace{\begin{pmatrix} \sqrt{5} & \frac{4}{5}\sqrt{5}\\ 0 & \frac{3}{5}\sqrt{5}\end{pmatrix} }}\]
2)From \(A=Q\Lambda Q^{T}\) where \(Q\) is the matrix which contains as its columns the normalized eigenvectors of \(A\) and \(\Lambda \) contains in its diagonal the eigenvalues of \(A\). First start by finding eigenvalues and eigenvectors of \(A\)
\(\begin{pmatrix} 5 & 4\\ 4 & 5 \end{pmatrix} \rightarrow \) eigenvectors:\(\left \{ \begin{pmatrix} -1\\ 1 \end{pmatrix} \right \} \leftrightarrow 1,\left \{ \begin{pmatrix} 1\\ 1 \end{pmatrix} \right \} \leftrightarrow 9\)
Hence \(Q=\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} \rightarrow \)normalize columns\(\rightarrow Q=\frac{1}{\sqrt{2}}\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} ,\Lambda =\begin{pmatrix} 1 & 0\\ 0 & 9 \end{pmatrix} \)
So, verify first that the above is correct:
\(A=\frac{1}{\sqrt{2}}\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0\\ 0 & 9 \end{pmatrix}\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} \frac{1}{\sqrt{2}}=\frac{1}{2}\allowbreak \times \begin{pmatrix} 10 & 8\\ 8 & 10 \end{pmatrix} =\allowbreak \begin{pmatrix} 5 & 4\\ 4 & 5 \end{pmatrix} \)
Correct. So we write \(R=\left ( \sqrt{\Lambda }Q^{T}\right ) =\sqrt{\begin{pmatrix} 1 & 0\\ 0 & 9 \end{pmatrix} }\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} \frac{1}{\sqrt{2}}=\begin{pmatrix} 1 & 0\\ 0 & 3 \end{pmatrix}\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} \frac{1}{\sqrt{2}}=\allowbreak \begin{pmatrix} -1 & 1\\ 3 & 3 \end{pmatrix} \frac{1}{\sqrt{2}}\)
Hence \begin{align*} A & =R^{T}R\\ & =\overset{R^{T}=Q\sqrt{\Lambda }}{\overbrace{\frac{1}{\sqrt{2}}\allowbreak \begin{pmatrix} -1 & 3\\ 1 & 3 \end{pmatrix} }}\overset{R=\sqrt{\Lambda }Q^{T}}{\overbrace{\begin{pmatrix} -1 & 1\\ 3 & 3 \end{pmatrix} \frac{1}{\sqrt{2}}}} \end{align*}
\(3)\) now find \(R=\left ( Q\sqrt{\Lambda }Q^{T}\right ) \)
\(R=\frac{1}{\sqrt{2}}\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} \sqrt{\begin{pmatrix} 1 & 0\\ 0 & 9 \end{pmatrix} }\frac{1}{\sqrt{2}}\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} =\frac{1}{2}\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0\\ 0 & 3 \end{pmatrix}\begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} =\allowbreak \begin{pmatrix} 2 & 1\\ 1 & 2 \end{pmatrix} \)
Hence \begin{align*} A & =R^{T}R\\ & =\begin{pmatrix} 2 & 1\\ 1 & 2 \end{pmatrix} ^{T}\begin{pmatrix} 2 & 1\\ 1 & 2 \end{pmatrix} \\ & =\overset{R^{T}=Q\sqrt{\Lambda }Q^{T}}{\overbrace{\begin{pmatrix} 2 & 1\\ 1 & 2 \end{pmatrix} }}\overset{R=Q\sqrt{\Lambda }Q^{T}}{\overbrace{\begin{pmatrix} 2 & 1\\ 1 & 2 \end{pmatrix} }} \end{align*}
problem: if \(A\) is SPD and C is nonsignular, prove that \(B=C^{T}AC\) is also SPD
solution: Since \(A\) is SPD, then it has positive eigenvalues.
Since \(B\) is similar to \(A\) (given), then \(B\) has the same eigenvalues as \(A\), Hence \(B\) also has all its eigenvalues positive.
Hence by theorem 6B, \(B\) is symmetric positive definite.