Problem: Find the inverse of \(\ A_{1}=\begin{bmatrix} 0 & 2\\ 3 & 0 \end{bmatrix} ,A_{2}=\begin{bmatrix} 2 & 0\\ 4 & 2 \end{bmatrix} ,A_{3}=\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \)
Answer:
Using the formula
\[\begin{bmatrix} a & b\\ c & d \end{bmatrix} ^{-1}=\frac{1}{ad-bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix} \]
Hence
\begin{align*} A_{1}^{-1} & =\begin{bmatrix} 0 & 2\\ 3 & 0 \end{bmatrix} ^{-1}=\frac{-1}{6}\begin{bmatrix} 0 & -2\\ -3 & 0 \end{bmatrix} =\begin{bmatrix} 0 & \frac{1}{3}\\ \frac{1}{2} & 0 \end{bmatrix} \\ A_{2}^{-1} & =\begin{bmatrix} 2 & 0\\ 4 & 2 \end{bmatrix} ^{-1}=\frac{1}{4}\begin{bmatrix} 2 & 0\\ -4 & 2 \end{bmatrix} =\begin{bmatrix} \frac{1}{2} & 0\\ -1 & \frac{1}{2}\end{bmatrix} \\ A_{3}^{-1} & =\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} ^{-1}=\frac{1}{\cos ^{2}\theta +\sin ^{2}\theta }\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} =\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} \end{align*}
Problem: (a) Find the inverses of the permutation matrices \(P_{1}=\begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 0 \end{bmatrix} \) and \(P_{2}=\begin{bmatrix} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix} \)
(b) Explain for permutation why \(P^{-1}\) is always the same as \(P^{T}\). Show that the \(1^{\prime }s\) are in the right place to give \(PP^{T}=I\)
Solution:
(a) When \(P_{1}=\begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 0 \end{bmatrix} \) is applied to a matrix \(A\) its effect on \(A\) is to replace the first row of by the 3rd row of, and to replace the 3rd row by the first row at the same time. As an example \(\begin{bmatrix} X\\ Y\\ Z \end{bmatrix} \overset{P_{1}}{\Rightarrow }\) \(\begin{bmatrix} Z\\ Y\\ X \end{bmatrix} \). Hence to reverse this effect, we need to perform the same operation again, i.e. replace the first row by the 3rd row and replace the 3rd row by the first, but this is \(P_{1}\) itself. Hence \(\begin{bmatrix} Z\\ Y\\ X \end{bmatrix} \overset{P_{1}}{\Rightarrow }\begin{bmatrix} X\\ Y\\ Z \end{bmatrix} \)
Therefor \(P_{1}^{-1}=P_{1}\)
\(P_{2}=\begin{bmatrix} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix} \) says to replace first row by the 3rd row, and to replace the second row by the first and to replace the 3rd row by the second. For example \(\begin{bmatrix} X\\ Y\\ Z \end{bmatrix} \overset{P_{2}}{\Rightarrow }\) \(\begin{bmatrix} Z\\ X\\ Y \end{bmatrix} \), Hence to reverse it, we need to replace the first row by the second, and to replace the second row by the 3rd and to replace the 3rd row by the first at the same time. Hence \(P_{2}^{-1}=\begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{bmatrix} \)
(b) In a permutation matrix \(P\), each row will have at most one non-zero entry with value of \(1.\)
Consider the entry \(P_{i,j}=1\). This entry will cause row \(i\) to be replaced by row \(j.\) Hence to reverse the effect, we need to replace row \(j\) by row \(i\), or in other words, we need to have the entry \((j,i)\) in the inverse matrix be \(1\). But this is the same as transposing \(P\), since in a transposed matrix the entry \(\left ( i,j\right ) \) goes to \(\left ( j,i\right ) \)
Hence \[ \fbox{$P^{-1}=P^{T}$}\]
Now Let \(PP^{T}=C\), where \(P,P^{T}\), are permutation matrices (in other words, each row of \(P,P^{T}\) is all zeros, except for one entry with value of \(1\).)
Hence the entry \(C\left ( i,i\right ) \) will be \(1\) whenever \(A\left ( i,j\right ) =B\left ( j,i\right ) =1\), This is from the definition of matrix multiplication, element by element view, since \(C\left ( k,l\right ) ={\displaystyle \sum \limits _{j=1}^{N}} P\left ( k,j\right ) \times P^{T}\left ( j,l\right ) \) but \(P\left ( k,j\right ) \times P^{T}\left ( j,l\right ) =0\) for all entries except when the entry \(P\left ( k,j\right ) =1\), and at the same time \(P^{T}\left ( j,l\right ) =1\), but since \(P^{T}\) is the transpose of \(P\), then whenever \(P\left ( k,j\right ) =1\) then \(P^{T}\left ( j,l\right ) =1\) only when \(k=l\).
Hence this leads to \(C\left ( k,k\right ) =1\) with all other entries in \(C\) being zero.
i.e. \[ \fbox{$C=PP^{T}=I$}\]
Problem: Give examples of \(A\) and \(B\) such that
(a) \(A+B\) is not invertible although \(A\) and \(B\) are invertible
(b) \(A+B\) is invertible although \(A\) and \(B\) are not invertible
(c) All of \(A,B\) and \(A+B\) are invertible
In the last case use \(A^{-1}\left ( A+B\right ) B^{-1}=B^{-1}+A^{-1}\) to show that \(C=B^{-1}+A^{-1}\) is also invertible and find a formula for \(C^{-1}\)
Answer:
(a)\(A=\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} ,B=\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \)
Here \(A,B\) are both invertible (\(Det\left ( A\right ) =-1\,,Det\left ( B\right ) =1\), while \(Det\left ( A+B\right ) =Det\begin{bmatrix} 1 & 1\\ 1 & 1 \end{bmatrix} =0\)) i.e. \(\left ( A+B\right ) \) not invertible.
(b)\(A=\begin{bmatrix} 1 & 0\\ 0 & 0 \end{bmatrix} ,B=\begin{bmatrix} 0 & 0\\ 0 & 1 \end{bmatrix} \,,\)Here \(A,B\) are both non-invertible (\(Det\left ( A\right ) =0\,,Det\left ( B\right ) =0\), while \(Det\left ( A+B\right ) =Det\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} =1\)) i.e. \(\left ( A+B\right ) \) invertible.
(c)\(A=\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} ,B=\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix} \)Here \(A,B\) are both invertible (\(Det\left ( A\right ) =1\,,Det\left ( B\right ) =-1\), and \(Det\left ( A+B\right ) =Det\begin{bmatrix} 2 & 1\\ 1 & 1 \end{bmatrix} =1\)) i.e. \(\left ( A+B\right ) \) invertible also.
Now need to find a formula for \(C^{-1}.\)
Since \(C=B^{-1}+A^{-1},\) then \begin{align*} C^{-1} & =\left ( B^{-1}+A^{-1}\right ) ^{-1}\\ & =(A^{-1}\left ( A+B\right ) B^{-1})^{-1}\\ & =\left ( B^{-1}\right ) ^{-1}\left ( A^{-1}\left ( A+B\right ) \right ) ^{-1}\\ & =B\left ( \left ( A+B\right ) ^{-1}\left ( A^{-1}\right ) ^{-1}\right ) \\ & =\fbox{$B\left ( A+B\right ) ^{-1}A$} \end{align*}
btw, reading around, found a paper called ”On the inverse of the sum of Matrices” by Kenneth Meler, gives this formula
\[ \left ( X+Y\right ) ^{-1}=X^{-1}-\frac{1}{1+trace(YX^{-1})}X^{-1}YX^{-1}\]
(But this is valid when Y has rank 1?)
Problem: If \(A=L_{1}D_{1}U_{1}\) and \(A=L_{2}D_{2}U_{2}\) prove that \(L_{1}=L_{2},D_{1}=D_{2}\) and \(U_{1}=U_{2}\). If \(A\) is invertible, the factorization is unique.
(a) Derive the equation \(L_{1}^{-1}L_{2}D_{2}=D_{1}U_{1}U_{2}^{-1}\) and explain why one side is lower triangular and the other side is upper triangular.
(b) Compare the main diagonals and then compare the off-diagonals.
Solution:
This question is asking to show that the \(LDV\) decomposition is unique.
Proof by contradiction: Assume the decomposition is not unique. Hence there exist \(\left [ L\right ] \left [ D\right ] \left [ V\right ] \) and \(\left [ \hat{L}\right ] \left [ \hat{D}\right ] \left [ \hat{V}\right ] \) decompositions of \(A\).
Hence we write \begin{align*} A & =\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\end{bmatrix} \\ & =\left [ L\right ] \left [ D\right ] \left [ V\right ] \mathbf{=}\left [ \hat{L}\right ] \left [ \hat{D}\right ] \left [ \hat{V}\right ] \\ & =\begin{bmatrix} 1 & 0\\ L_{21} & 1 \end{bmatrix}\begin{bmatrix} D_{11} & 0\\ 0 & D_{22}\end{bmatrix}\begin{bmatrix} 1 & V_{12}\\ 0 & 1 \end{bmatrix} \mathbf{=}\begin{bmatrix} 1 & 0\\ \hat{L}_{21} & 1 \end{bmatrix}\begin{bmatrix} \hat{D}_{11} & 0\\ 0 & \hat{D}_{22}\end{bmatrix}\begin{bmatrix} 1 & \hat{V}_{12}\\ 0 & 1 \end{bmatrix} \\ & =\begin{bmatrix} 1 & 0\\ L_{21} & 1 \end{bmatrix}\begin{bmatrix} D_{11} & D_{11}V_{12}\\ 0 & D_{22}\end{bmatrix} \mathbf{=}\begin{bmatrix} 1 & 0\\ \hat{L}_{21} & 1 \end{bmatrix}\begin{bmatrix} \hat{D}_{11} & \hat{D}_{11}\hat{V}_{12}\\ 0 & \hat{D}_{22}\end{bmatrix} \\ & =\begin{bmatrix} D_{11} & D_{11}V_{12}\\ L_{21}D_{11} & L_{21}D_{11}V_{12}+D_{22}\end{bmatrix} \mathbf{=}\begin{bmatrix} \hat{D}_{11} & \hat{D}_{11}\hat{V}_{12}\\ \hat{L}_{21}\hat{D}_{11} & \hat{L}_{21}\hat{D}_{11}\hat{V}_{12}+\hat{D}_{22}\end{bmatrix} \end{align*}
Since both of the above 2 matrix are equal to the same matrix \(A\), compare elements to elements from the above.
Then we see that \(D_{11}=a_{11}\), and \(\hat{D}_{11}=a_{11}\), hence\[ \fbox{$D_{11}=\hat{D}_{11}$}\]
Similarly, \(D_{11}V_{12}=a_{12}\), and \(\hat{D}_{11}\hat{V}_{12}=a_{12}\), therefor \(D_{11}V_{12}=\hat{D}_{11}\hat{V}_{12}\). But from above we showed that \(D_{11}=\hat{D}_{11}\), hence \[ \fbox{$V_{12}=\hat{V}_{12}$}\]
Similarly, \(L_{21}D_{11}=a_{21}\) and \(\hat{L}_{21}\hat{D}_{11}=a_{21}\) hence \(L_{21}D_{11}=\hat{L}_{21}\hat{D}_{11}\), but from above we showed that \(D_{11}=\hat{D}_{11}\), hence \[ \fbox{$L_{21}=\hat{L}_{21}$}\]
Finally, \(L_{21}D_{11}V_{12}+D_{22}=a_{22}\), and \(\hat{L}_{21}\hat{D}_{11}\hat{V}_{12}+\hat{D}_{22}=a_{22}\), hence \(L_{21}D_{11}V_{12}+D_{22}=\hat{L}_{21}\hat{D}_{11}\hat{V}_{12}+\hat{D}_{22}\), but since from above we showed that \(D_{11}=\hat{D}_{11}\) and \(V_{12}=\hat{V}_{12}\) and \(L_{21}=\hat{L}_{21}\), hence this means that \[ \fbox{$D_{22}=\hat{D}_{22}$}\]
Hence we showed that all the elements of \(L\) are equal to all the elements of \(\hat{L}\), i.e. \(L=\hat{L}\), similarly \(V=\hat{V}\) and \(D=\hat{D}\), But this is a contradiction that the decomposition is not unique. Hence the decomposition is unique.
(a) Start with
\[ L_{1}D_{1}U_{1}=L_{2}D_{2}U_{2}\]
right multiply both sides by \(U_{2}^{-1}\)
\begin{align*} L_{1}D_{1}U_{1}U_{2}^{-1} & =L_{2}D_{2}U_{2}U_{2}^{-1}\\ L_{1}D_{1}U_{1}U_{2}^{-1} & =L_{2}D_{2} \end{align*}
left multiply both sides by \(L_{1}^{-1}\)
\[ L_{1}^{-1}L_{1}D_{1}U_{1}U_{2}^{-1}=L_{1}^{-1}L_{2}D_{2}\]
Hence
\[ \fbox{$D_{1}U_{1}U_{2}^{-1}=L_{1}^{-1}L_{2}D_{2}$}\]
Since \(U\) is an upper triangle matrix, then its inverse is also an upper triangle matrix. When 2 upper triangle matrices are multiplied with each others, the result is a diagonal matrix (a matrix with non-zero elements only on the diagonal). Hence \(U_{1}U_{2}^{-1}\) is a diagonal matrix. But \(D_{1}\) is a diagonal matrix, and the product of 2 diagonal matrices is a diagonal matrix. Hence \(D_{1}U_{1}U_{2}^{-1}\) is a diagonal matrix.
Now looking at the RHS. \(L\) is a lower triangle matrix. Hence its inverse is a lower triangle matrix. The product of 2 lower triangle matrices is a diagonal matrix. But \(D_{2}\) is a diagonal matrix, and the product of 2 diagonal matrices is a diagonal matrix. Hence \(L_{1}^{-1}L_{2}D_{2}\) is a diagonal matrix.
But a diagonal matrix is both an upper and a lower diagonal matrices. Hence one can label one side as lower diagonal matrix and the other side as upper diagonal matrix.
(b) The main diagonals contain the pivots. The off diagonals are the same, all zeros.
Problem: If \(A\) has row 1+row2=row3, show that \(A\) is not invertible.
(a) Explain why \(Ax=\left ( 1,0,0\right ) \) cannot have a solution
(b) Which right-hand sides (\(b_{1},b_{2},b_{3}\)) might allow a solution for \(Ax=b\)?
(c) What happens to row 3 in elimination?
Answer:
One answer is to use the row view. This leads to geometrical reasoning. A row represents an equation of some hyperplane in \(n\) dimensional space. For \(n=3,\) this represents a plane. Since we are told 2 planes add to a third, hence we only need to consider 2 planes to obtain a solution. The solution (if one exist) of 2 planes is a line (2 planes if they interest make a line). Hence we can not have a single point as a solution. Hence \(\left ( 1,0,0\right ) \) can not be a solution. This is the same as saying that a matrix whose rows (or columns) are not all linearly independent to each others is not invertible.
Another way to show this is by construction.
If row1+row2=row3, then A is not invertible since when using Gaussian elimination the method will fail. To show how and why, and W.L.O.G., consider the following \(3\times 3\) matrix where row1+row2=row3
\[ A=\begin{bmatrix} a & b & c\\ d & e & f\\ a+d & b+e & c+f \end{bmatrix} \]
Elimination using \(l_{21}=\frac{d}{a}\) gives
\[\begin{bmatrix} a & b & c\\ 0 & e-b\left ( \frac{d}{a}\right ) & f-c\left ( \frac{d}{a}\right ) \\ a+d & b+e & c+f \end{bmatrix} \]
Elimination using \(l_{31}=\frac{a+d}{a}\) gives
\begin{align*} \begin{bmatrix} a & b & c\\ 0 & e-b\left ( \frac{d}{a}\right ) & f-c\left ( \frac{d}{a}\right ) \\ 0 & \left ( b+e\right ) -b\left ( \frac{a+d}{a}\right ) & \left ( c+f\right ) -c\left ( \frac{a+d}{a}\right ) \end{bmatrix} & =\begin{bmatrix} a & b & c\\ 0 & \frac{ea-bd}{a} & \frac{fa-cd}{a}\\ 0 & \left ( b+e\right ) -\frac{ab+db}{a} & \left ( c+f\right ) -\frac{ca+cd}{a}\end{bmatrix} \\ & =\begin{bmatrix} a & b & c\\ 0 & \frac{ea-bd}{a} & \frac{fa-cd}{a}\\ 0 & \frac{ab+ae}{a}-\frac{ab+db}{a} & \frac{ca+fa}{a}-\frac{ca+cd}{a}\end{bmatrix} \\ & =\begin{bmatrix} a & b & c\\ 0 & \frac{ea-bd}{a} & \frac{fa-cd}{a}\\ 0 & \frac{\left ( ab+ae\right ) -\left ( ab+db\right ) }{a} & \frac{\left ( ca+fa\right ) -\left ( ca+cd\right ) }{a}\end{bmatrix} \\ & =\begin{bmatrix} a & b & c\\ 0 & \frac{ea-bd}{a} & \frac{fa-cd}{a}\\ 0 & \frac{ea-bd}{a} & \frac{fa-cd}{a}\end{bmatrix} \end{align*}
we see that we are unable to eliminate this any more. row 2 now is the same as row 3. Trying to zero out entry (3,2) will cause entry (3,3) to become zero as well since \(l_{32}=1\) in this case. Hence we will get the third row to be all zeros. and hence no unique solution can result.
(a) To answer this part, consider the row view of \(A\mathbf{x}=\mathbf{b}.\) The solution is where the 3 planes intersects, which is a point.
Since first row+second row=third row, then we only have 2 planes here to consider and not 3. which are row 1 and row 2 only. Hence the solution is a line and not a point (2 planes can have only have a line as a solution). Hence it is not possible to have the solution be a point when we have only 2 planes in 3 dimensional space.
(b) The right hand side of \(\left [ 0,0,0\right ] \) would allow a solution of \(x=\left [ 0,0,0\right ] \)
(c) In elimination, as shown above, row 3 will be the same as row 2. Hence it is not possible to zero out entry (3,2) and finish elimination.
Problem: If the product \(M=ABC\) of the three square matrices is invertible, then \(A,B,C,\) are invertible. Find a formula for \(B^{-1}\) that involves \(M^{-1}\), \(A\) and \(C\)
solution:
Since \(M\) is invertible, then \begin{align*} M^{-1} & =\left ( ABC\right ) ^{-1}\\ & =\left ( BC\right ) ^{-1}A^{-1}\\ & =C^{-1}B^{-1}A^{-1} \end{align*}
Left multiply both sides by \(C\)
\begin{align*} CM^{-1} & =CC^{-1}B^{-1}A^{-1}\\ CM^{-1} & =B^{-1}A^{-1} \end{align*}
right multiply both sides by \(A\)
\begin{align*} CM^{-1}A & =B^{-1}A^{-1}A\\ & =B^{-1} \end{align*}
Hence
\[ \fbox{$B^{-1}=CM^{-1}A$}\]
Problem: Find \(A^{T}\) and \(A^{-1}\) and \(\left ( A^{-1}\right ) ^{T}\) and \(\left ( A^{T}\right ) ^{-1}\) for
\(A=\begin{bmatrix} 1 & 0\\ 9 & 3 \end{bmatrix} ,B=\begin{bmatrix} 1 & c\\ c & 0 \end{bmatrix} \)
Solution:
\[ A^{T}=\begin{bmatrix} 1 & 9\\ 0 & 3 \end{bmatrix} \]
\[ A^{-1}=\frac{1}{3}\begin{bmatrix} 3 & 0\\ -9 & 1 \end{bmatrix} =\begin{bmatrix} 1 & 0\\ -3 & \frac{1}{3}\end{bmatrix} \]
\begin{align*} \left ( A^{-1}\right ) ^{T} & =\begin{bmatrix} 1 & -3\\ 0 & \frac{1}{3}\end{bmatrix} \\ \left ( A^{T}\right ) ^{-1} & =\left ( A^{-1}\right ) ^{T}=\begin{bmatrix} 1 & -3\\ 0 & \frac{1}{3}\end{bmatrix} \end{align*}
\[ B^{T}=\begin{bmatrix} 1 & c\\ c & 0 \end{bmatrix} \]
\[ B^{-1}=\frac{1}{-c^{2}}\begin{bmatrix} 0 & -c\\ -c & 1 \end{bmatrix} =\begin{bmatrix} 0 & \frac{1}{c}\\ \frac{1}{c} & -\frac{1}{c^{2}}\end{bmatrix} \]
\begin{align*} \left ( B^{-1}\right ) ^{T} & =\begin{bmatrix} 1 & \frac{1}{c}\\ \frac{1}{c} & -\frac{1}{c^{2}}\end{bmatrix} \\ \left ( B^{T}\right ) ^{-1} & =\left ( B^{-1}\right ) ^{T}=\begin{bmatrix} 1 & \frac{1}{c}\\ \frac{1}{c} & -\frac{1}{c^{2}}\end{bmatrix} \end{align*}
Problem: Verify that \(\left ( AB\right ) ^{T}\) equals \(B^{T}A^{T}\) but these are different from \(A^{T}B^{T}\)
\(A=\begin{bmatrix} 1 & 0\\ 2 & 1 \end{bmatrix} ,B=\begin{bmatrix} 1 & 3\\ 0 & 1 \end{bmatrix} ,AB=\begin{bmatrix} 1 & 3\\ 2 & 7 \end{bmatrix} \)
in case \(AB=BA\) (not generally true!) how do you prove that \(B^{T}A^{T}=A^{T}B^{T}?\)
Solution:
\[ \left ( AB\right ) ^{T}=\left ( \begin{bmatrix} 1 & 0\\ 2 & 1 \end{bmatrix}\begin{bmatrix} 1 & 3\\ 0 & 1 \end{bmatrix} \right ) ^{T}=\begin{bmatrix} 1 & 3\\ 2 & 7 \end{bmatrix} ^{T}=\begin{bmatrix} 1 & 2\\ 3 & 7 \end{bmatrix} \]
\[ B^{T}A^{T}=\begin{bmatrix} 1 & 3\\ 0 & 1 \end{bmatrix} ^{T}\begin{bmatrix} 1 & 0\\ 2 & 1 \end{bmatrix} ^{T}=\begin{bmatrix} 1 & 0\\ 3 & 1 \end{bmatrix}\begin{bmatrix} 1 & 2\\ 0 & 1 \end{bmatrix} =\begin{bmatrix} 1 & 2\\ 3 & 7 \end{bmatrix} \]
Hence \(\left ( AB\right ) ^{T}=B^{T}A^{T}\) but
\[ A^{T}B^{T}=\begin{bmatrix} 1 & 0\\ 2 & 1 \end{bmatrix} ^{T}\begin{bmatrix} 1 & 3\\ 0 & 1 \end{bmatrix} ^{T}=\begin{bmatrix} 1 & 2\\ 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0\\ 3 & 1 \end{bmatrix} =\begin{bmatrix} 7 & 2\\ 3 & 1 \end{bmatrix} \neq B^{T}A^{T}\]
Now to show that if \(AB=BA\) then \(A^{T}B^{T}=B^{T}A^{T}\)
Since we are given that \(AB=BA\,\), then take the transpose of each side
\[ \left ( AB\right ) ^{T}=\left ( BA\right ) ^{T}\]
But \(\left ( XY\right ) ^{T}=Y^{T}X^{T}\), hence applying this rule to each side of the above , we obtain the result needed
\[ B^{T}A^{T}=A^{T}B^{T}\]
Problem: If \(A=A^{T}\) and \(B=B^{T}\), which of these matrices are certainly symmetric?
(a)\(A^{2}-B^{2}\) (b)\(\left ( A+B\right ) \left ( A-B\right ) \) (c)\(ABA\) (d)\(ABAB\)
Solution:
If \(A\) and \(B\) are symmetric matrices, then \(A-B\) and \(A+B\) are symmetric. Call this rule (1).
To show this, WLOG, we can use \(2\times 2\) matrices and write
\(A=\begin{bmatrix} a & b\\ b & c \end{bmatrix} ,B=\begin{bmatrix} e & f\\ f & g \end{bmatrix} \Rightarrow A+B=\begin{bmatrix} a+e & b+f\\ b+f & c+g \end{bmatrix} \) which is symmetric.
and \(A-B=\begin{bmatrix} a-e & b-f\\ b-f & c-g \end{bmatrix} \)which is symmetric.
(a)\(\ \)WLOG, we can check on a general \(2\times 2\) symmetric matrix \(A:\)
\(A^{2}=\begin{bmatrix} a & b\\ b & c \end{bmatrix}\begin{bmatrix} a & b\\ b & c \end{bmatrix} =\begin{bmatrix} a^{2}+b^{2} & ab+bc\\ ba+cb & b^{2}+c^{2}\end{bmatrix} \) which is symmetric.
Hence if \(A\) is symmetric, then \(A^{2}\) is symmetric. Similarly, \(\ \)if \(B\) is symmetric, then \(B^{2}\). Hence using rule (1) above, it follows that \(A^{2}-B^{2}\) is symmetric
(b) Using rule (1), \(\left ( A+B\right ) \) is symmetric and so is \(\left ( A-B\right ) \), hence we need to see if the product of two symmetric matrices is always symmetric or not. WLOG, we can check on a \(2\times 2\) symmetric matrices.
\(X=\begin{bmatrix} a & b\\ b & c \end{bmatrix} ,Y=\begin{bmatrix} e & f\\ f & g \end{bmatrix} \Rightarrow XY=\begin{bmatrix} a & b\\ b & c \end{bmatrix}\begin{bmatrix} e & f\\ f & g \end{bmatrix} =\begin{bmatrix} ae+bf & af+bg\\ be+cf & bf+cg \end{bmatrix} \) which is
in general (unless \(af+bg=be+cf)\) which is not true in general.
(c)To check on \(ABA\), from part(b) we showed that the product of 2 symmetric matrices is not necessarily symmetric, hence \(AB\) is not necessarily symmetric\(,\) Let \(AB=X\), then the above is the same as asking if \(XA\) is always symmetric when \(X\) is not necessarily symmetric and \(A\) is symmetric. The answer is NO. To show, WLOG, try to a general \(2\times 2\) matrices.
Let \(X=\begin{bmatrix} a & b\\ c & d \end{bmatrix} \) where \(c\neq b\), and \(A=\begin{bmatrix} e & f\\ f & g \end{bmatrix} \Rightarrow XA=\begin{bmatrix} a & b\\ c & d \end{bmatrix}\begin{bmatrix} e & f\\ f & g \end{bmatrix} =\begin{bmatrix} ae+bf & af+bg\\ ce+df & cf+dg \end{bmatrix} \)
which is NOT symmetric in general (unless \(af+bg=ce+df\) )
(d) To check on \(ABAB\), From (b) we showed that the product of 2 symmetric matrices is NOT necessarily symmetric, hence \(AB\) is NOT necessarily symmetric. Hence this is asking if the product of 2 matrices, both not necessarily symmetric is certainly symmetric or not. Hence the answer is NOT symmetric. (if the product of 2 symmetric matrices is not necessarily symmetric, then the product of 2 matrices who are not symmetric is also not necessarily symmetric).
Problem: Write out the \(LDU=LDL^{T}\) factors of \(A\) in equation (6) when \(n=4.\) Find the determinant as the product of the pivots in \(D.\)
Solution:
for \(n=4\), \[ A=\begin{bmatrix} 2 & -1 & 0 & 0\\ -1 & 2 & -1 & 0\\ 0 & -1 & 2 & -1\\ 0 & 0 & -1 & 2 \end{bmatrix} \]
To start LU decomposition, write the augmented matrix
\(\begin{bmatrix} 2 & -1 & 0 & 0\\ -1 & 2 & -1 & 0\\ 0 & -1 & 2 & -1\\ 0 & 0 & -1 & 2 \end{bmatrix} \overset{l_{21}=\frac{-1}{2}}{\Rightarrow }\begin{bmatrix} 2 & -1 & 0 & 0\\ 0 & \frac{3}{2} & -1 & 0\\ 0 & -1 & 2 & -1\\ 0 & 0 & -1 & 2 \end{bmatrix} \overset{l_{32}=\frac{-2}{3}}{\Rightarrow }\begin{bmatrix} 2 & -1 & 0 & 0\\ 0 & \frac{3}{2} & -1 & 0\\ 0 & 0 & \frac{4}{3} & -1\\ 0 & 0 & -1 & 2 \end{bmatrix} \)
\(\overset{l_{43}=\frac{-3}{4}}{\Rightarrow }\begin{bmatrix} 2 & -1 & 0 & 0\\ 0 & \frac{3}{2} & -1 & 0\\ 0 & 0 & \frac{4}{3} & -1\\ 0 & 0 & 0 & \frac{5}{4}\end{bmatrix} ,\)hence
\[ U=\begin{bmatrix} 2 & -1 & 0 & 0\\ 0 & \frac{3}{2} & -1 & 0\\ 0 & 0 & \frac{4}{3} & -1\\ 0 & 0 & 0 & \frac{5}{4}\end{bmatrix} \]
and \[ L=\begin{bmatrix} 1 & 0 & 0 & 0\\ \frac{-1}{2} & 1 & 0 & 0\\ 0 & \frac{-2}{3} & 1 & 0\\ 0 & 0 & \frac{-3}{4} & 1 \end{bmatrix} \]
and now we need to make the diagonal elements of \(U\) be all \(1^{\prime }s\), hence the \(D\) matrix is
\[ D=\begin{bmatrix} 2 & 0 & 0 & 0\\ 0 & \frac{3}{2} & 0 & 0\\ 0 & 0 & \frac{4}{3} & 0\\ 0 & 0 & 0 & \frac{5}{4}\end{bmatrix} \]
and the \(V\) matrix is
\[ V=\begin{bmatrix} 1 & -\frac{1}{2} & 0 & 0\\ 0 & 1 & -\frac{3}{2} & 0\\ 0 & 0 & 1 & -\frac{4}{3}\\ 0 & 0 & 0 & 1 \end{bmatrix} \]
Hence
\[ LDV=\begin{bmatrix} 1 & 0 & 0 & 0\\ \frac{-1}{2} & 1 & 0 & 0\\ 0 & \frac{-2}{3} & 1 & 0\\ 0 & 0 & \frac{-3}{4} & 1 \end{bmatrix}\begin{bmatrix} \fbox{$2$} & 0 & 0 & 0\\ 0 & \fbox{$\frac{3}{2}$} & 0 & 0\\ 0 & 0 & \fbox{$\frac{4}{3}$} & 0\\ 0 & 0 & 0 & \fbox{$\frac{5}{4}$}\end{bmatrix}\begin{bmatrix} 1 & -\frac{1}{2} & 0 & 0\\ 0 & 1 & -\frac{3}{2} & 0\\ 0 & 0 & 1 & -\frac{4}{3}\\ 0 & 0 & 0 & 1 \end{bmatrix} \]
which is equal to \(LDL^{T}\)
Now the determinant of \(A\) can be found as the products of the pivots, which are along the diagonal of the \(D\) matrix \[ 2\times \frac{3}{2}\times \frac{4}{3}\times \frac{5}{4}=\allowbreak 5 \]
Problem: Find the \(5\times 5\) matrix \(A_{o}(h=\frac{1}{6})\) that approximates
\[ -\frac{d^{2}u}{dx^{2}}=f\left ( x\right ) \]
with boundary conditions \(u^{\prime }(0)=u^{\prime }\left ( 1\right ) =0\)
replace these boundary conditions by \(u_{0}=u_{1}\) and \(u_{6}=u_{5}\). Check that your \(A_{o}\) times the constant vector \(\left [ C,C,C,C,C\right ] \) yields zero. \(A_{o}\) is singular. Analogously, if \(u\left ( x\right ) \) is a solution of the continuos problem, then so is \(u\left ( x\right ) +C\)
Solution:
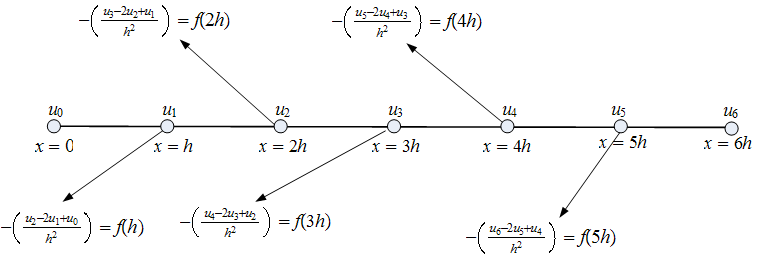
Using the approximation \(\frac{d^{2}u}{dx^{2}}\approx \frac{u\left ( x+h\right ) -2u\left ( x\right ) +u\left ( x-h\right ) }{h^{2}}\) we write the above ODE for each internal point as shown in this diagram

Hence we have the following 5 equations (one equation generated per one internal node)
\begin{align*} -u_{2}+2u_{1}-u_{0} & =h^{2}f\left ( h\right ) \\ -u_{3}+2u_{2}-u_{1} & =h^{2}f\left ( 2h\right ) \\ -u_{4}+2u_{3}-u_{2} & =h^{2}f\left ( 3h\right ) \\ -u_{5}+2u_{4}-u_{3} & =h^{2}f\left ( 4h\right ) \\ -u_{6}+2u_{5}-u_{4} & =h^{2}f\left ( 5h\right ) \end{align*}
Since the boundary condition given is \(u^{\prime }(0)\), this means that the rate of change of \(u\) at the boundary is zero (insulation). Hence the value of the dependent variable does not change at the boundary. This is another way of say that \(u_{0}=u_{1}\). The same on the other side, where \(u_{6}=u_{5}\). Doing these replacement into the above equations we obtain the following
\begin{align*} -u_{2}+u_{1} & =h^{2}f\left ( h\right ) \\ -u_{3}+2u_{2}-u_{1} & =h^{2}f\left ( 2h\right ) \\ -u_{4}+2u_{3}-u_{2} & =h^{2}f\left ( 3h\right ) \\ -u_{5}+2u_{4}-u_{3} & =h^{2}f\left ( 4h\right ) \\ u_{5}-u_{4} & =h^{2}f\left ( 5h\right ) \end{align*}
Written in Matrix form, and given \(h=\frac{1}{6}\)
\[\begin{bmatrix} 1 & -1 & 0 & 0 & 0\\ -1 & 2 & -1 & 0 & 0\\ 0 & -1 & 2 & -1 & 0\\ 0 & 0 & -1 & 2 & -1\\ 0 & 0 & 0 & -1 & 1 \end{bmatrix}\begin{bmatrix} u_{1}\\ u_{2}\\ u_{3}\\ u_{4}\\ u_{5}\end{bmatrix} =\frac{1}{36}\begin{bmatrix} f\left ( h\right ) \\ f\left ( 2h\right ) \\ f\left ( 3h\right ) \\ f\left ( 4h\right ) \\ f\left ( 5h\right ) \end{bmatrix} \]
Now Check that \(A_{0}\times B=0\) where \(B\) is some constant vector \(\left [ C,C,C,C,C\right ] \)
\[\begin{bmatrix} 1 & -1 & 0 & 0 & 0\\ -1 & 2 & -1 & 0 & 0\\ 0 & -1 & 2 & -1 & 0\\ 0 & 0 & -1 & 2 & -1\\ 0 & 0 & 0 & -1 & 1 \end{bmatrix}\begin{bmatrix} C\\ C\\ C\\ C\\ C \end{bmatrix} =\begin{bmatrix} 0\\ 0\\ 0\\ 0\\ 0 \end{bmatrix} \]
Problem: Compare the pivots in direct elimination to those with partial pivoting for \(A=\begin{bmatrix} 0.001 & 0\\ 1 & 1000 \end{bmatrix} \) (this is actually an example that needs rescaling before elimination)
Solution:
Direct elimination \(\begin{bmatrix} 0.001 & 0\\ 1 & 1000 \end{bmatrix} \overset{l_{21}=1000}{\Rightarrow }\begin{bmatrix} \fbox{$0.001$} & 0\\ 0 & \fbox{$1000$}\end{bmatrix} \)
Partial pivoting. Switch rows first \(\Rightarrow \begin{bmatrix} 1 & 1000\\ 0.001 & 0 \end{bmatrix} ,\) now apply elimination
\(\begin{bmatrix} 1 & 1000\\ 0.001 & 0 \end{bmatrix} \overset{l_{21}=0.001}{\Rightarrow }\begin{bmatrix} \fbox{$1$} & 1000\\ 0 & \fbox{$-1$}\end{bmatrix} \)
The pivots in direct elimination are \(\left \{ 0.001,1000\right \} \), while when using partial pivoting \(\left \{ 1,-1\right \} \)