Problem: Which of the following subsets of \(R^{3}\) are actually subsets?
(a) The plane of vectors \(\left ( b_{1},b_{2},b_{3}\right ) \) with the first component \(b_{1}=0\)
(b)The plane of vectors \(b\) with \(b_{1}=1\)
(c)The plane of vectors \(b\) with \(b_{2}b_{3}=0\) (this is the union of the 2 subspaces, plane \(b_{2}=0\) and plane \(b_{3}=0\))
(d)All combinations of 2 vectors \(\left ( 1,1,0\right ) \) and \(\left ( 2,0,1\right ) \)
(e)The plane of vectors \(\left ( b_{1},b_{2},b_{3}\right ) \) which satisfies \(b_{3}-b_{2}+3b_{1}=0\)
answer:
(a) This is the plane \(y-z\) which \(x=0.\) The zero vector is in this plane. Adding any 2 vectors will remain this this plane, and scaling any vector will remain in the plane. Hence this is a subspace of \(R^{3}\)
(b) This is a plane parallel to the \(y-z\) plane, but at an offset of 1. Hence this plane does not include the origin. Hence this is not a subspace of \(R^{3}\)
(c) This is the union of the plane \(x-z\) and the plane \(x-y\), hence this plane is the \(x-axis\) only. The zero vector is one this line. Adding any 2 vectors will remain this this line, and scaling any vector will remain one the line. Hence this is a subspace of \(R^{3}\)
(d) Since these 2 vectors are linearly independent (There is no way to multiply one of these vectors by a scalar to obtain the second one) hence they are bases vectors for an \(R^{2}\) space within \(R^{3}\). Since the zero vector can be reached by these 2 vectors (they both originate from the origin), Hence this is a subspace of \(R^{3}\) (by definition, bases vectors can be used to reach any vector in the space these bases vectors span), and since the problem did not give any restriction to the region within this subspace in which we can reach, hence closed under addition and scaler multiplication).
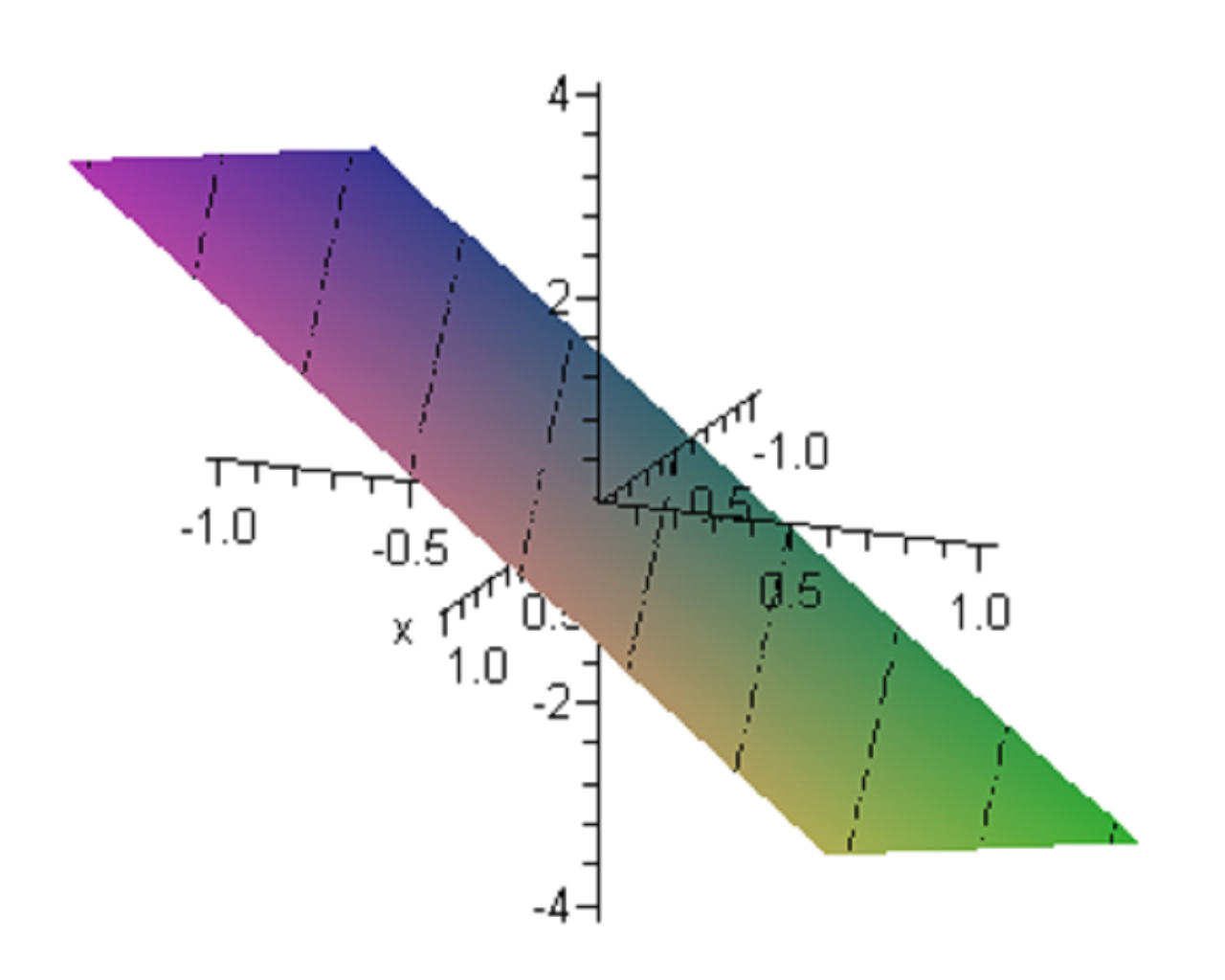
(e)These vectors span a plane through the origin in which each vector satisfy the equation on its coordinates such that \(b_{3}-b_{2}+3b_{1}=0\). This an illustration on this plane \(z=y-3x\)

The zero vector is in this subspace. OK
Any scaled vector on this plane will remain in this plane. OK.
The additions of any 2 vectors in this plane will remain in this plane. (the plane is ’flat’, i.e. it has zero curvature, hence it is not possible to leave this plane using combination of vectors which lie in the plane itself).
Hence this is a subspace of \(R^{3}\)
question: Describe the column space and the null space of these matrices
\(A=\begin{bmatrix} 1 & -1\\ 0 & 0 \end{bmatrix} ,B=\begin{bmatrix} 1 & -1 & 3\\ 1 & 2 & 3 \end{bmatrix} ,C=\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix} \)
answer:
A)
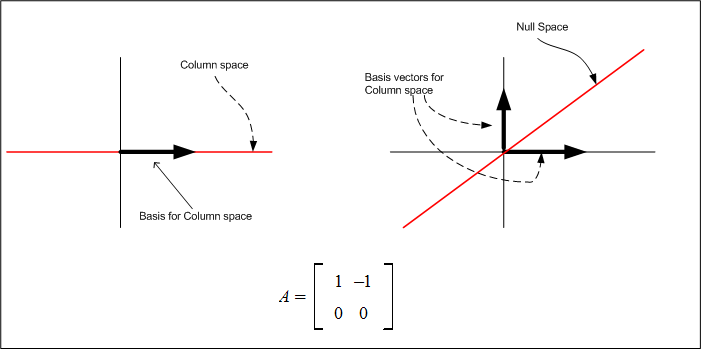
The column space is the space reached by vectors represented by the columns of the matrix. For matrix \(A\) these are the vectors \(\begin{pmatrix} 1\\ 0 \end{pmatrix} ,\begin{pmatrix} -1\\ 0 \end{pmatrix} \), hence the space is the set of all vectors \(a\begin{pmatrix} 1\\ 0 \end{pmatrix} +b\begin{pmatrix} -1\\ 0 \end{pmatrix} \), for \(a,b\in R\), hence this is the whole \(x-axis\) line. i.e. \[ C\left ( A\right ) =\begin{pmatrix} 1\\ 0 \end{pmatrix} \]
i.e. the vector \((1,0)\) is the basis for the column space of A.
The null space is the solution to \(Ax=0,\) hence we have \(\begin{bmatrix} 1 & -1\\ 0 & 0 \end{bmatrix} \) \(\begin{bmatrix} x\\ y \end{bmatrix} =\begin{bmatrix} 0\\ 0 \end{bmatrix} \), which gives \(x-y=0\) which means \(x=1\) and \(y=1\) (or \(x=c\), \(y=c\) for any scalar \(c\)). i.e. \(N\left ( A\right ) =\begin{pmatrix} 1\\ 1 \end{pmatrix} \) i.e. the vector \(\left ( 1,1\right ) \) is the basis vector for the Null space of A.
Hence the null space is a line whose coordinates are \(\left ( c,c\right ) \)
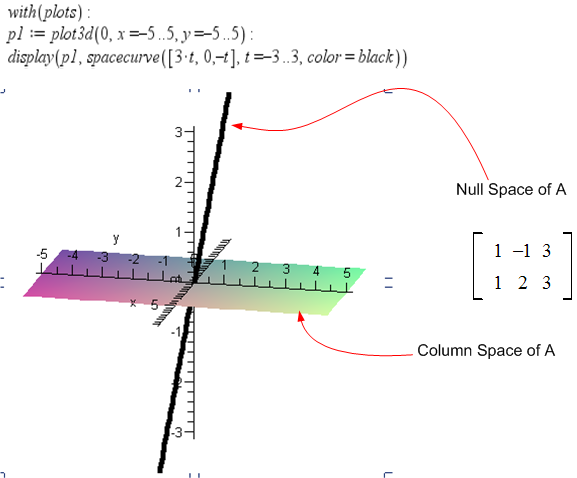
\(B=\begin{bmatrix} 1 & -1 & 3\\ 1 & 2 & 3 \end{bmatrix} \)
The first and third columns do not produce any new basis, hence the column space is spanned by the first and the second columns only. These 2 columns are linearly independent, hence they are basis. Since we have 2 basis vectors, and we in are in \(R^{3}\) space, hence these 2 columns will span all of the subspace \(R^{2}\) and a basis that can be used to span the column space are the the standard basis \(\begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} ,\begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix} \)
The null space is the solution to \(Ax=0\), or \(\begin{bmatrix} 1 & -1 & 3\\ 1 & 2 & 3 \end{bmatrix}\begin{pmatrix} x_{1}\\ x_{2}\\ x_{3}\end{pmatrix} =\begin{pmatrix} 0\\ 0 \end{pmatrix} \), hence we obtain \(x_{1}-x_{2}+3x_{3}=0,\) and \(x_{1}+2x_{2}+3x_{3}=0\)
If we try \(x_{1}=3,x_{2}=0,x_{3}=-1\), we see that this solution satisfies these 2 equations. Hence \(\begin{pmatrix} 3\\ 0\\ -1 \end{pmatrix} \) is a basis vector that spans the null space of \(A\). The null space of \(A\) is a line through the origin. Any point on the line \(3x+0y-z=0\) is in the null space of \(A\)
\(C=\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix} \)
The column space is the space that can be reached by combination of the columns. Since the columns are the zero vectors, hence the space that can be spanned is empty. Hence \(C\left ( A\right ) =\{\}\)
Since the dimension of the space reached by the column space basis + the dimension of the space reach by the null space basis must equal the number of columns which is 3, hence the null space must be \(R^{3}\), and the basis that can be used are the standard basis \[\begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} ,\begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix} ,\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \]
(a) Let \(\mathbf{x}=\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} ,\mathbf{y}=\begin{pmatrix} y_{1}\\ y_{2}\end{pmatrix} \)
note: in these problems use the zero vector as \(\begin{pmatrix} -1\\ -1 \end{pmatrix} \)
Rules (1),(2) can easily be verified to be valid under the new sum rule.
For rule (3), we get \begin{align*} \mathbf{x} & \mathbf{=}\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} +\mathbf{0}\\ & =\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} +\begin{pmatrix} -1\\ -1 \end{pmatrix} \\ & =\begin{pmatrix} x_{1}-1+\fbox{$1$}\\ x_{2}-1+\fbox{$1$}\end{pmatrix} \\ & =\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} \\ & =\mathbf{x} \end{align*}
hence rule(3) is NOT broken.
For rule (4) we have \begin{align*} \mathbf{0} & =\mathbf{x+}\left ( -\mathbf{x}\right ) \\ & =\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} +\begin{pmatrix} -x_{1}\\ -x_{2}\end{pmatrix} \\ & =\begin{pmatrix} x_{1}-x_{1}-\fbox{$1$}\\ x_{2}-x_{2}-\fbox{$1$}\end{pmatrix} \\ & =\begin{pmatrix} -1\\ -1 \end{pmatrix} =\mathbf{0\ \ }\text{(using these rules)} \end{align*}
hence rule (4) is not broken.
Rules (5) and (6) are not affected since they involve only multiplication.
For rule (7) we have \begin{align*} c\left ( \mathbf{x}+\mathbf{y}\right ) & =c\left ( \begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} +\begin{pmatrix} y_{1}\\ y_{2}\end{pmatrix} \right ) \\ & =c\begin{pmatrix} x_{1}+y_{1}+\fbox{$1$}\\ x_{2}+y_{2}+\fbox{$1$}\end{pmatrix} \\ & =\begin{pmatrix} cx_{1}+cy_{1}+c\\ cx_{2}+cy_{2}+c \end{pmatrix} \\ & =\begin{pmatrix} cx_{1}\\ cx_{2}\end{pmatrix} +\begin{pmatrix} cy_{1}\\ cy_{2}\end{pmatrix} +\begin{pmatrix} c\\ c \end{pmatrix} \\ & =c\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} +c\begin{pmatrix} y_{1}\\ y_{2}\end{pmatrix} +c\begin{pmatrix} 1\\ 1 \end{pmatrix} \\ & =c\mathbf{x}+c\mathbf{y+}c\begin{pmatrix} 1\\ 1 \end{pmatrix} \\ & =c\left ( \mathbf{x}+\mathbf{y}\right ) +c\begin{pmatrix} 1\\ 1 \end{pmatrix} \end{align*}
but \(c\left ( \mathbf{x}+\mathbf{y}\right ) \neq c\left ( \mathbf{x}+\mathbf{y}\right ) +c\begin{pmatrix} 1\\ 1 \end{pmatrix} \), hence rule (7) is broken
For rule 8, \begin{align*} \left ( c_{1}+c_{2}\right ) \mathbf{x} & \mathbf{=}\left ( c_{1}+c_{2}\right ) \begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} \\ & =c_{1}\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} +c_{2}\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} \\ & =\begin{pmatrix} c_{1}x_{1}\\ c_{1}x_{2}\end{pmatrix} +\begin{pmatrix} c_{2}x_{1}\\ c_{2}x_{2}\end{pmatrix} \\ & =\begin{pmatrix} c_{1}x_{1}+c_{2}x_{1}+\fbox{$1$}\\ c_{1}x_{2}+c_{2}x_{2}+\fbox{$1$}\end{pmatrix} \\ & =\begin{pmatrix} c_{1}x_{1}+c_{2}x_{1}\\ c_{1}x_{2}+c_{2}x_{2}\end{pmatrix} +\begin{pmatrix} 1\\ 1 \end{pmatrix} \\ & =c_{1}\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} +c_{2}\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix} +\begin{pmatrix} 1\\ 1 \end{pmatrix} \\ & =\left ( c_{1}+c_{2}\right ) \mathbf{x+}\begin{pmatrix} 1\\ 1 \end{pmatrix} \end{align*}
but \(\left ( c_{1}+c_{2}\right ) \mathbf{x\neq }\) \(\left ( c_{1}+c_{2}\right ) \mathbf{x+}\begin{pmatrix} 1\\ 1 \end{pmatrix} \), hence rule (8) is broken.
Hence rules (7),(8) are broken