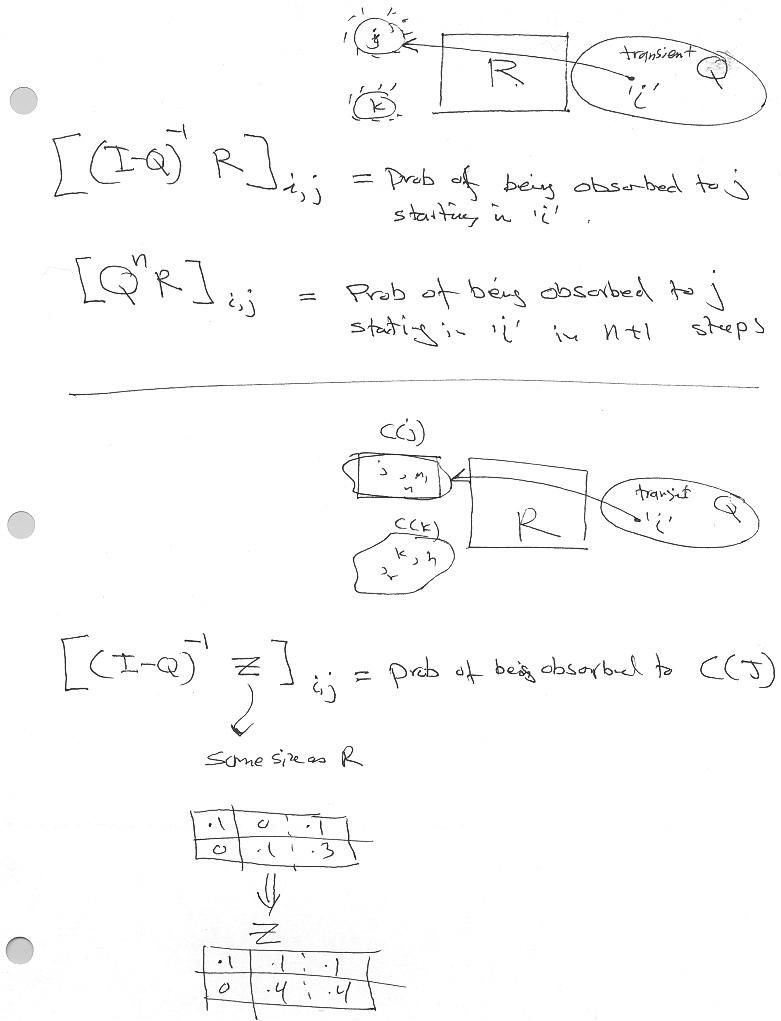-
up
-
This document in PDF
Study notes. Math 504 (Simulation), CSUF. spring
2008
spring 2008 Compiled on October 26, 2018 at 8:22am
Contents
1 some code I wrote for testing things...
-
expected_test.m
-
solving_3_dot_6,nb
-
A small note on using the left eigenvector of the one step transition matrix for a
regular chain to determine the limiting distribution trying_8_1_problem.nb
trying_8_1_problem.pdf
2 Definitions
Source of this block unknown and lost from the net:
Continuous Time Markov Chains Most of our models will be formulated as continuous time Markov chains. On this page we describe the workings of these processes and how we simulate them. Definition. We say that an event happens at rate r(t) if an occurence between times t and t + dt has probability about r(t)dt when dt is small. Fact. When r(t) is a constant r, the times t[i] between occurrences are independent exponentials with mean 1/r, and we have a Poisson process with rate r. Markov chains in continuous time are defined by giving the rates q(x,y) at which jumps occur from state x to state y. In many cases (including all our examples) q(x,y) can be written as p(x,y)Q where Q is a constant that represents the total jump rate. In this case we can construct the chain by taking one step according to the transition probability p(x,y) at each point of a Poisson process with rate Q. If we throw away the information about the exponential holding times in each state, the resulting sequence of states visited is a discrete time Markov chain, which is called the embedded discrete time chain. In our simulations, the total flip rate Q at any one time is a multiple of the number of sites, CQ. Since the number of sites is typically tens of thousands, we lose very little accuracy by simulating TCQ steps and calling the result the state at time T. To build the discrete time chain we must pick from the various transitions with probabilities proportional to their rates. In our particle systems we can do this by picking a site at random, applying a stochastic updating rule, and then repeating the procedure. Because of this, continuous time is occasionally referred to as asynchronous updating. This is to distinguish that porcedure from the synchronous updating of a discrete time process which updates all of the sites simultaneously.
2.1 Regular finite M.C.
definition 1: There exist some  such that
such that  has all positive entries
has all positive entries
definition 2: A regular finite chain is one which is irreducible and aperiodic
Notice that this means regular chain has NO transient states.
2.2 irreducible M.C.
A M.C. which contains one and only one closed set of states. Note that for finite MC, this
means all the states are recurrent. In otherwords, its state space contains no proper subset that
is closed.
2.3 Stationary distribution
This is the state vector  which contains the probability of each state that the MC could be in
the long term. For an irreducible MC, this is independent of the starting
which contains the probability of each state that the MC could be in
the long term. For an irreducible MC, this is independent of the starting  , however,
for a reducible MC, the Stationary distribution will be different for different initial
, however,
for a reducible MC, the Stationary distribution will be different for different initial

2.4 recurrent state
-
 . In otherwords, the probability of reaching state
. In otherwords, the probability of reaching state  eventually, starting
from state
eventually, starting
from state  is always certain.
is always certain.
-
 , in otherwords, since sum diverges, this means the probability to
return back to
, in otherwords, since sum diverges, this means the probability to
return back to  starting from
starting from  will always exist, not matter how large
will always exist, not matter how large  is (i.e.
sum terms never reach all zeros after some limiting value
is (i.e.
sum terms never reach all zeros after some limiting value  )
)
2.5 transient state
-
 . In otherwords, the probability of reaching state
. In otherwords, the probability of reaching state  eventually, starting
from state
eventually, starting
from state  is not certain. i.e. there will be a chance that starting from
is not certain. i.e. there will be a chance that starting from  , chain
will never again get back to state
, chain
will never again get back to state  .
.
-
 , in otherwords, since sum converges, this means the probability to
return back to
, in otherwords, since sum converges, this means the probability to
return back to  starting from
starting from  will NOT always exist (i.e. sum terms reach all
zeros after some limiting value
will NOT always exist (i.e. sum terms reach all
zeros after some limiting value  )
)
2.6 Positive recurrent state
A recurrent state where the expected number of steps to return back to the state is
finite.
2.7 Null recurrent state
A recurrent state where the expected number of steps to return back to the state is
infinite.
2.8 Period of state
GCD of the integers  such that
such that  . In otherwords, find all the steps MC will
take to return back to the same state, then find the GCD of these values. If the
GCD is
. In otherwords, find all the steps MC will
take to return back to the same state, then find the GCD of these values. If the
GCD is  , then the period is
, then the period is  and the state is called Aperiodic (does not have a
period).
and the state is called Aperiodic (does not have a
period).
2.9 Ergodic state
A state which is Aperiodic and positive recurrent. i.e. a recurrent state (with finite number of
steps to return) but it has no period.
2.10 First entrance time 
The number of steps needed to reach state  (first time) starting from transient state
(first time) starting from transient state

2.11 
This is the probability that it will take  steps to first reach state
steps to first reach state  starting from transient
state
starting from transient
state  . i..e
. i..e 
2.12 
This is the probability of reaching state  (for first time) when starting from transient state
(for first time) when starting from transient state
 . Hence
. Hence 
2.13 Closed set
A set of states, where if MC enters one of them, it can’t reach a state outside this set. i.e.
 whenever
whenever  and
and  , then set
, then set  is called closed set.
is called closed set.
2.14 Absorbing M.C.
All none-transient states are absorbing states. Hence the  matrix looks like
matrix looks like
 i.e.
i.e. ![[ ]
I 0
R Q](index-38e3259dc5d44a875f2449503a1480c3.svg)
2.15  Matrix
Matrix
Properties of a  matrix are: There is at least one row which sums to less than 1. And there is
a way to reach such row(s) from other others. and
matrix are: There is at least one row which sums to less than 1. And there is
a way to reach such row(s) from other others. and  as
as 
2.16 Balance equations
3 HOW TO finite Markov chain
3.1 How to find 
This is the probability it will take  steps to first reach state
steps to first reach state  from state
from state  . In Below
. In Below
 means the closed set which contains the state
means the closed set which contains the state  and
and  means the transient
set
means the transient
set
|
|
 , ,  |
use formula (1) below |
|
|
 , ,  |
 |
|
|
 , ,  Absorbing state Absorbing state | Calculate  where where  then the then the  entry of entry of  gives gives  |
|
|
 , ,  |
| Normally we are interested in finding expected number | of visits to  before absorbing. i.e before absorbing. i.e  . see below. Otherwise use (1) . see below. Otherwise use (1) |
|
|
|
| |
We can use  . Notice the subtle difference between
. Notice the subtle difference between  and
and  .
.
 gives the probability of needing
gives the probability of needing  steps to first reach
steps to first reach  from
from  , while
, while  gives
the probability of being in state
gives
the probability of being in state  after
after  steps leaving
steps leaving  . So with
. So with  could
have reached state
could
have reached state  before
before  steps, but left state
steps, but left state  and moved around, then
came back, as long as after
and moved around, then
came back, as long as after  steps exactly MC will be in state
steps exactly MC will be in state  . With
. With  this
is not allowed. The chain must reach state
this
is not allowed. The chain must reach state  the very first time in
the very first time in  steps from
leaving
steps from
leaving  . So in a sense,
. So in a sense,  is a more strict probability. Using the recursive
formula
is a more strict probability. Using the recursive
formula
 | (1) |
We can calculate  . We see that
. We see that  and so
and so  and
also
and
also
and
etc...
Hence knowing just the  matrix, we can always obtain values of the
matrix, we can always obtain values of the  for any
powers
for any
powers
However, using the following formula, from lecture notes 6.2 is easier

the  entry of
entry of  gives the probability of taking
gives the probability of taking  steps to first reaching
steps to first reaching  when
starting from transient state
when
starting from transient state 
 So use this formula. Just note this formula works only when
So use this formula. Just note this formula works only when
 is transient.
is transient.
question
: If  is NOT transient, and we asked to find what is the prob. it will take
is NOT transient, and we asked to find what is the prob. it will take  steps to first
reach state
steps to first
reach state  from state
from state  . Then use (1). right?
. Then use (1). right?
3.2 How to find 
This is the probability that chain will eventually reach state  given it starts in state
given it starts in state

|
|
|
|
 |
 |
|
|
 |
 |
|
|
 | | Use formula in page 5.5 lecture notes |
 |
 , hence just needs to find , hence just needs to find  |
 |
|
|
|
|
|
 |
![f = [(I − Q )−1 R]
ij i,j](index-3422b16845c3a5b136550a072676dcca.svg) |
|
|
|
|
 |
We know eventually  for for  , but can we talk about , but can we talk about  here? here? |
|
|
|
|
| |
3.3 How to find  the expected number of visits to j before absorbing?
the expected number of visits to j before absorbing?
Here,  and
and  Then
Then

The above gives the average number of visits to state  (also transient) before chain is
absorbed for first time.
(also transient) before chain is
absorbed for first time.
question: Note that if chain is regular, then all states communicates with each others and then
 and so
and so  can be found from the stationary distribution
can be found from the stationary distribution  ,
right?
,
right?
3.4 How to find average number of steps  between state
between state  and state
and state  ?
?
|
|
 |
 |
|
|
 |
does not make sense to ask this here? |
|
|
| |
3.5 How to find number of visits to a transient state?
Number of visits to transient state is a geometric distribution.

The expected number of visits to transient state  is
is

where  is the probability of visiting state
is the probability of visiting state  if chain starts in state
if chain starts in state 
4 Some useful formulas


4.1 Law of total probability

4.2 Conditional (Bayes) formula

4.3 Inverse of a 2 by 2 matrix
![[ ]
[ ]−1 d − b
a b − c a
= -----------
c d ad − bc](index-1c5d3e37ae0c225127148be51942b4ab.svg)
4.4 
The above says that for a regular finite MC, where a stationary probability exist (and is
unique), then it is inverse of the mean number of steps between visits  to state
to state  in steady
state.
in steady
state.
4.5 
The above says that for a regular M.C. there exist a stationary probability distribution

4.6 Poisson random variable
 is number of events that occur over some period of time.
is number of events that occur over some period of time.
 is a Poisson random variable if
is a Poisson random variable if
-

-
Independent increments
-

Where  is the average number of events that occur over the same period that we are asking
for the probability of this number of events to occur. Hence remember to adjust
is the average number of events that occur over the same period that we are asking
for the probability of this number of events to occur. Hence remember to adjust  accordingly
if we are given
accordingly
if we are given  as rate (i.e. per unit time).
as rate (i.e. per unit time).
4.7 Poisson random Process
 is a Poisson random variable if
is a Poisson random variable if
-

-
Independent increments
-

Where  is the average number of events that occur in one unit time. So
is the average number of events that occur in one unit time. So  is
random variable which is the number of events that occur during interval of length
is
random variable which is the number of events that occur during interval of length

The probability that ONE event occure in the next

interval, when the interval is very small, is

This can be seen by setting  in the definition and using series expansion for
in the definition and using series expansion for  and
then letting
and
then letting 
Expected value of Poisson random variable:  . For a process,
. For a process,  where
where
 is the rate.
is the rate.
4.8 Exponential random variable
 is random variable which is the time between events where the number of events occur as
Poisson distribution,
is random variable which is the time between events where the number of events occur as
Poisson distribution,
pdf: 

![∫t
−λs [ −λs]t [ −λt ] − λt
P (T < t) = λe ds = − e 0 = − e − 1 = 1 − e
0](index-42b4661a86e8ed7c2c57efb0c1d577b0.svg)
pdf=derivative of CDF
Probability that the waiting time for  events to occur
events to occur  is a GAMMA distribution.
is a GAMMA distribution.

5 Diagram to help understanding
5.1 Continouse time Markov chain
 is the parameter (rate) for the exponential distributed random variable which represents the
time in that state. Hence The probability that system remains in state
is the parameter (rate) for the exponential distributed random variable which represents the
time in that state. Hence The probability that system remains in state  for time larger than
for time larger than
 is given by
is given by

 Jump probability
Jump probability  for
for  . This is the probability of going from state
. This is the probability of going from state  to
state
to
state  (once the process leaves state
(once the process leaves state  )
)
 FOrward Komogolv equation
FOrward Komogolv equation
 , let
, let  , hence
, hence  hence
hence  therefore
therefore

 Balance equations
Balance equations

This is ’flow out’ = ’flow in’.
This equation can also be obtaind more easily I think from  Where
Where  is the matrix
made up from the
is the matrix
made up from the  and the
and the  on the diagonal. Just write then down, and at the end add
on the diagonal. Just write then down, and at the end add
 to find
to find