HOME

Contents

1 Problem 1 (section 1.3,#1, page 40)

problem: Find the general solution of the following differential equations

(m) \(u^{\prime \prime }+\omega ^{2}u=\sin \beta t\), \(\omega \neq \beta \)

solution:

We start by assuming \(\omega \) is real, hence \(\omega ^{2}\) must be positive.

Now, the general solution is

Where \(u_{1}\left ( t\right ) ,u_{2}\left ( t\right ) \) are the 2 independent solutions of the homogeneous differential equation

and \(u_{p}\left ( t\right ) \) is the particular solution.

To find \(u_{1}\left ( t\right ) \) and \(u_{2}\left ( t\right ) \), we assume the homogeneous solution is \(u_{h}\left ( t\right ) =Ae^{mt}\) for some constants \(A,m\) and substitute this assumed solution in the ODE. We obtain the characteristic equation \(Am^{2}e^{mt}+\omega ^{2}Ae^{mt}=0\rightarrow m^{2}+\omega ^{2}=0\rightarrow m^{2}=-\omega ^{2}\) or \(m=\pm i\omega \), hence \(u_{1}\left ( t\right ) =A_{1}e^{i\omega t}\) and \(u_{2}\left ( t\right ) =A_{2}e^{-i\omega t}\).

Since the homogeneous solution is a linear combination of all the independent solutions, we take the sum and the difference of these solutions, and using Euler relation which converts the complex exponential to the trigonometric \(\sin \) and \(\cos \) functions we obtain

and we now write

Now to obtain \(u_{p}\left ( t\right ) \), we use the method of undetermined coefficients. Assume

and plug into the original ODE, we obtain

Hence by comparing coefficients we obtain

Since \(\omega \neq \beta \) (given), then \(\omega ^{2}-\beta ^{2}\neq 0\,\), hence this must mean the following

Therefor, the particular solution now can be written as

Hence the general solution, which is \(y\left ( t\right ) =y_{h}\left ( t\right ) +y_{p}\left ( t\right ) \) is given by

Where \(c_{1}\) and \(c_{2}\) are constants that can be found from the initial conditions.

2 Problem 2 (section 1.3,#1, page 40)

problem: Find the general solution of the following differential equations

(n) \(u^{\prime \prime }+\omega ^{2}u=\cos \omega t\)

solution:

First, let the forcing function be called \(f\left ( t\right ) \), hence \(f\left ( t\right ) =\cos \omega t\) in this example.

From (m) we found the homogeneous solution to be \(u_{h}\left ( t\right ) =c_{1}u_{1}\left ( t\right ) +c_{2}u_{2}\left ( t\right ) \) where

and

Now to find the particular solution we can not use the method of undetermined coefficients since the forcing frequency is the same as the undamped natural frequency of the system \(\omega \) and this will lead to the denominator going to zero. Hence use the method of variation of parameters which is a general method to find particular solution which will work with this case.

Where \(W\) is the Wronskian of \(u_{1},u_{2}\) given by \(W=u_{1}u_{2}^{\prime }-u_{2}u_{1}^{\prime }\)

Hence \(W\left ( t\right ) =\cos \omega t\left ( \omega \cos \omega t\right ) -\sin \omega t\left ( -\omega \sin \omega t\right ) =\omega \left ( \cos ^{2}\omega t+\sin ^{2}\omega t\right ) =\omega \)

Hence

We now evaluate \(I_{1}\) and \(I_{2}\). Start with the easy one, \(I_{2}\)

and now \(I_{1}\)

We can use integration by parts (do it twice) or use an trigonometric identity. From tables, Using the formula of

so if we let \(\lambda =2\omega t\) and \(\zeta =0\) we obtain the integrand above, hence

Substitute into \(I_{1}\)

Therefor

Hence the general solution is

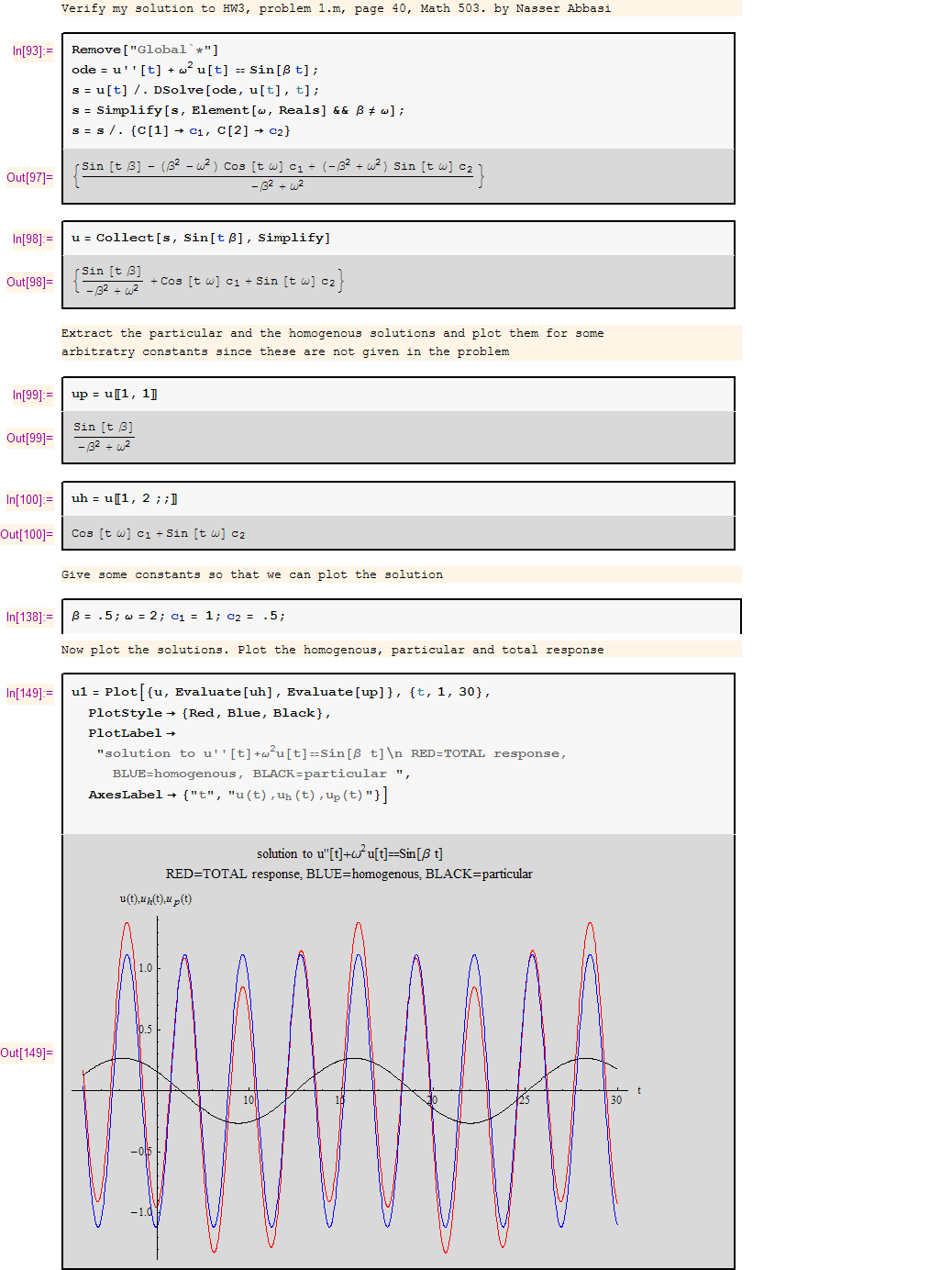
Verify using Mathematica