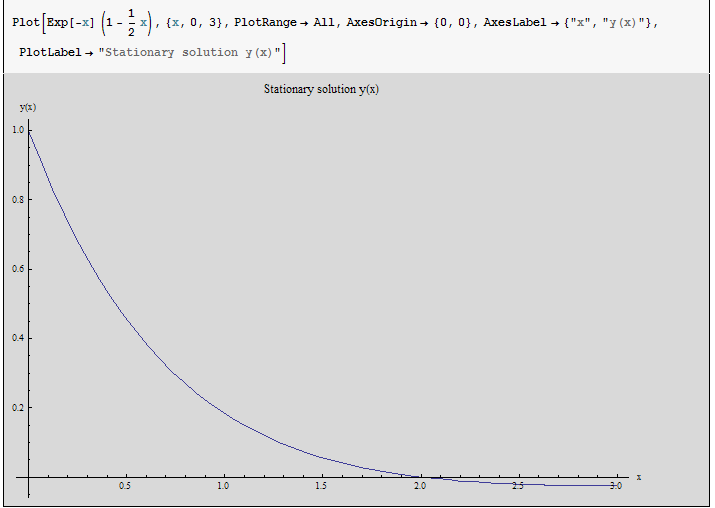
problem: Find extrermals for the following functional:
(b) \(J\left ( y\right ) =\int _{0}^{3}e^{2x}\left ( y^{\prime 2}-y^{2}\right ) dx\)
\(y\left ( 0\right ) =1,y\left ( 3\right ) =\)free
Solution:
Starting from first principles. First the preliminary standard setup:
Let \(J:\left ( A\subset V\right ) \rightarrow \mathbb {R} \), where \(A\) is the set of admissible functions, and \(V:C^{2}\left [ a,b\right ] \), hence \(A=\left \{ y\in V:\ y\left ( a\right ) =0,y\left ( b\right ) =\text {free}\right \} \)
Let \(v\left ( x\right ) \) be the set \(A_{d}\left ( y\right ) \) of the permissible directions defined as \(A_{d}\left ( y\right ) =\left \{ v\in V:y+tv\in A\right \} \) for some real scalar \(-\xi <t<\xi \)
And \(L_{y}\left ( x,y,y^{\prime }\right ) \equiv \frac {\partial L}{\partial y}L\left ( x,y,y^{\prime }\right ) \) and \(L_{y^{\prime }}\left ( x,y,y^{\prime }\right ) \equiv \frac {\partial L}{\partial y^{\prime }}L\left ( x,y,y^{\prime }\right ) \)
Now we write
Therefor a necessary condition for \(y\left ( x\right ) \in A\) to be a local minimum for the functional \(J\left ( y\right ) \) is that \(\delta J\left ( y,v\right ) =0\) for all \(v\in A_{d}\), which means
Integrating by parts the second term above results in the general expression for the necessary condition for \(y\left ( x\right ) \) to be a local minimum for \(J\left ( y\right ) \), which is
Since \(v\left ( a\right ) =0\), the second term above simplifies, and the above equation becomes
Now we apply the following argument: Out of all functions \(v\in A_{d}\), we can find a set which has the property such that \(v\left ( b\right ) =0\). For these \(v^{\prime }s\) only (1) becomes
Where now we apply the other standard argument: Since the above is true for every arbitrary \(v\) (but remember now \(v\) is such that \(v\left ( b\right ) =0,\) but since there are so many such \(v^{\prime }s\) still, then the argument still holds) , then it must mean that
This will generate a second order ODE, which we will solve, with the boundary conditions \(y\left ( 0\right ) =1\)
But we need another boundary condition. Then we hold off solving this for one moment. Let us now consider those functions \(v\in A_{d}\) which have the property that \(v\left ( b\right ) \neq 0.\) For these \(v\)’s, and for the second term in (1) to become zero, we now must have
Now from (3) we have \(\frac {\partial L}{\partial y^{\prime }}=\frac {\partial }{\partial y^{\prime }}e^{2x}\left ( y^{\prime 2}-y^{2}\right ) =2e^{2x}y^{\prime }\), which means
Hence
This gives us the second boundary condition we needed to solve (2).
Hence to summarize the problem becomes that of solving for \(y\) given
with the boundary conditions \(y\left ( 0\right ) =1\) and \(y^{\prime }\left ( 3\right ) =0\)
Now (2) can be written as
Hence
Assume \(y=Ae^{mx}\,\), hence the characteristic equation is \(m^{2}+2m+1=0\rightarrow m=\frac {-b\pm \sqrt {b^{2}-4ac}}{2a}=\frac {-2\pm \sqrt {4-4}}{2}=\)\(-1\)
Since we have repeated root, then the solution is
When \(x=0\,,\ y=1\), hence \(c_{1}=1\)
when \(x=3,y^{\prime }=0,\) hence \(0=-e^{-3}+c_{2}\left ( e^{-3}-3e^{-3}\right ) \rightarrow c_{2}=-\frac {e^{-3}}{e^{-3}\left ( 2\right ) }\rightarrow \)\(c_{2}=-\frac {1}{2}\)
Hence the solution is
or

problem: determine the natural boundary condition at \(x=b\) for the variational problem defined by \(J\left ( y\right ) =\int _{a}^{b}L\left ( x,y,y^{\prime }\right ) dx+G\left ( y\left ( b\right ) \right ) \) where \(y\in C^{2}\left [ a,b\right ] ,y\left ( a\right ) =y_{0}\) and \(G\) is a given differentiable function on \(\mathbb {R} \)
Solution:
Starting from first principles, first the preliminary standard setup.
Let \(J:\left ( A\subset V\right ) \rightarrow \mathbb {R} \), where \(A\) is the set of admissible functions, and \(V:C^{2}\left [ a,b\right ] \) Hence \(A=\left \{ y\in V:\ y\left ( a\right ) =0,y\left ( b\right ) =free\right \} .\)Let \(v\left ( x\right ) \) be a set \(A_{d}\left ( y\right ) \) of permissible directions defined as \(A_{d}\left ( y\right ) =\left \{ v\in V:y+tv\in A\right \} \) for some real scalar \(-\xi <t<\xi \), and Let \(L_{y}\left ( x,y,y^{\prime }\right ) \equiv \frac {\partial L}{\partial y}L\left ( x,y,y^{\prime }\right ) \), and \(L_{y^{\prime }}\left ( x,y,y^{\prime }\right ) \equiv \frac {\partial L}{\partial y^{\prime }}L\left ( x,y,y^{\prime }\right ) \)
Now we write
Therefor a necessary condition for \(y\left ( x\right ) \in A\) to be a local minimum for \(J\left ( y\right ) \) is that \(\delta J\left ( y,v\right ) =0\) for all \(v\in A_{d}\), which means
Integrating the second term in the integral above by parts results in the general expression for the necessary condition for \(y\left ( x\right ) \) to be a local minimum for \(J\left ( y\right ) \), which is
Hence
Since \(y\left ( a\right ) =y_{0}\), we must have \(v\left ( a\right ) =0\), then the above simplifies to
Let us now consider those functions \(v\in A_{d}\) which have the property that \(v\left ( b\right ) \neq 0.\) For these \(v\)’s, for the second term in (1) to become zero, we now must have
Hence
Hence the natural boundary condition on \(y\left ( x\right ) \) at \(x=b\) must satisfy the above. (I do not see how can one go further without being given what \(L\) and \(G\) are.)