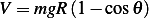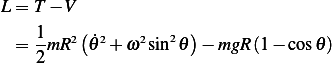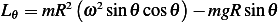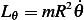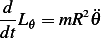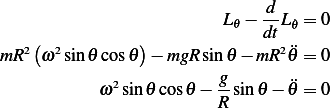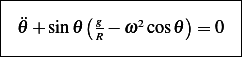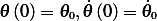HOME
HW 6 Mathematics 503, Mathematical Modeling, CSUF ,
June 24, 2007
Nasser M. Abbasi
June 15, 2014
Contents
1 Problem 1 (section 3.5,#9, page 197)
problem:
Consider a simple plane pendulum with a bob of mass  attached to a string of length
attached to a string of length 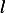 . After the
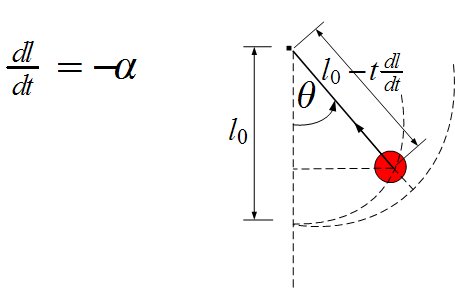
pendulum is set in motion the string is shortened by a constant rate
. After the
pendulum is set in motion the string is shortened by a constant rate 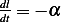 . Formulate Hamilton's principle
and determine the equation of motion. Compare the Hamiltonian to the total energy. Is energy
conserved?
. Formulate Hamilton's principle
and determine the equation of motion. Compare the Hamiltonian to the total energy. Is energy
conserved?
Solution:
Assume initial string length is 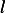 , and assume
, and assume 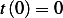 , then at time
, then at time 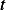 we have
we have
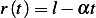
K.E. First note that
and
Now
P.E.
Hence
Hence
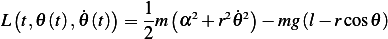 | (1) |
Hence the Euler-Lagrange equations are
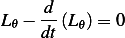 | (2) |
But
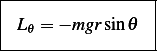
and
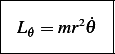
and
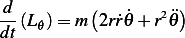
But 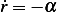 , the above becomes
, the above becomes
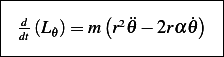
Hence 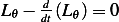 becomes
becomes
Hence the ODE becomes, after dividing by common factor 
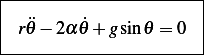
This is a second order nonlinear differential equation. Notice that when 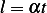 it will mean that the string
has been pulled all the way back to the pivot and
it will mean that the string
has been pulled all the way back to the pivot and 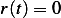 . So when running the solution it needs to run from
. So when running the solution it needs to run from
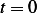 up to
up to 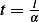 .
.
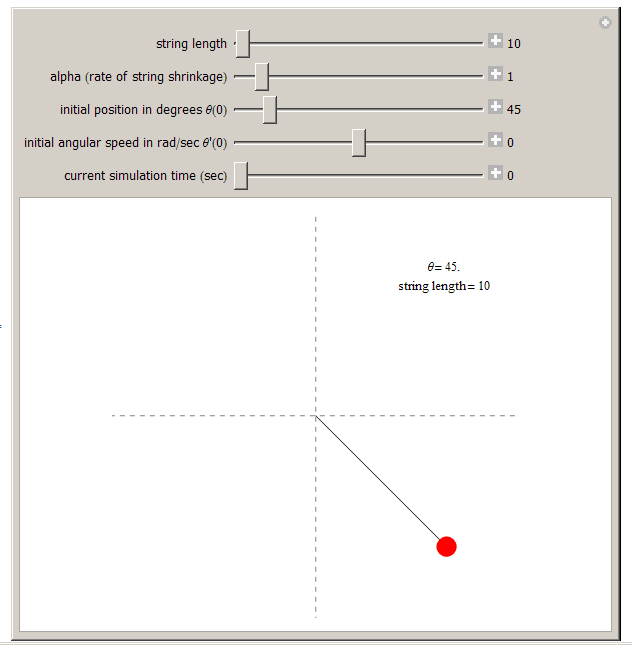
A small simulation was done for the above solution which can be run for different parameters to see the
effect more easily. Here is a screen shot.
Now we need to determine the Hamiltonian of the system.
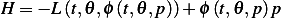 | (3) |
Where we define a new variable 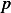 called the canonical momentum by
called the canonical momentum by
Hence
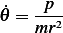
This implies that
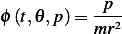
Then from (1) and (3), we now calculate 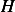
Hence the Hamiltonian is
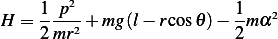 | (5) |
Now we are asked to compare 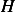 to the total energy. The total instantaneous energy of the system is
to the total energy. The total instantaneous energy of the system is
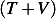 , hence we need to determine if
, hence we need to determine if 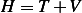 or not.
or not.
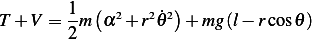 | (6) |
To make comparing (5) and (6) easier, I need to either replace 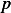 by
by 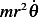 in (5) or replace
in (5) or replace 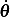 by
by 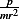 .
Lets do the later, hence
.
Lets do the later, hence 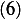 becomes
becomes
If 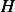 is the total energy, then (7)-(6) should come out to be zero, lets find out
is the total energy, then (7)-(6) should come out to be zero, lets find out
Hence we see that
Hence 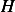 does not represents the total energy, and the
energy of the system is not conserved.
does not represents the total energy, and the
energy of the system is not conserved.
2 Problem 1 (section 3.5,#9, page 197)
problem: A bead of mass  slides down the rim of a circular hoop of radius
slides down the rim of a circular hoop of radius 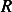 . The hoop stands vertically
and rotates about its diameter with angular velocity
. The hoop stands vertically
and rotates about its diameter with angular velocity 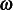 . Determine the equation of motion of the
bead.
. Determine the equation of motion of the
bead.
Answer:
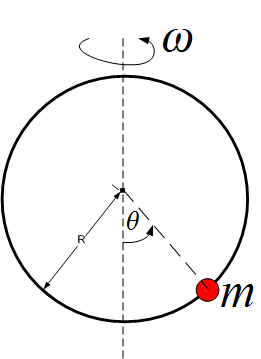
Kinetic energy 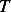 is made up of 2 components, one due to motion of the bead along the hoop itself
with speed
is made up of 2 components, one due to motion of the bead along the hoop itself
with speed 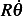 , and another due to motion with angular speed
, and another due to motion with angular speed 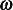 which has speed given by
which has speed given by
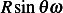
Hence
P.E. 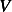 is due to the bead movement up and down the hoop, which is the standard
is due to the bead movement up and down the hoop, which is the standard 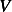 for a pendulum given
by
for a pendulum given
by
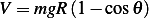
Hence
Hence
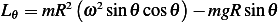
and
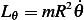
Hence
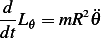
Hence
Hence the ODE is
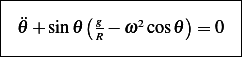
With initial conditions 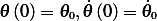
 attached to a string of length
attached to a string of length 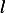 . After the
pendulum is set in motion the string is shortened by a constant rate
. After the
pendulum is set in motion the string is shortened by a constant rate 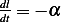 . Formulate Hamilton's principle
and determine the equation of motion. Compare the Hamiltonian to the total energy. Is energy
conserved?
. Formulate Hamilton's principle
and determine the equation of motion. Compare the Hamiltonian to the total energy. Is energy
conserved?
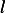 , and assume
, and assume 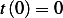 , then at time
, then at time 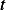 we have
we have
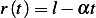
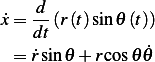
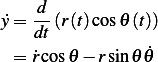
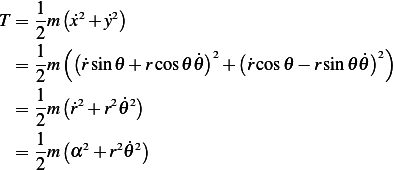
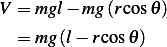
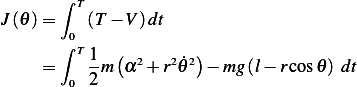
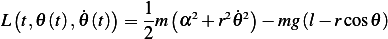
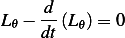
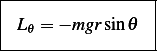
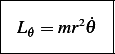
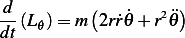
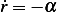 , the above becomes
, the above becomes
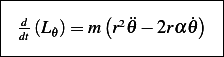
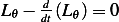 becomes
becomes
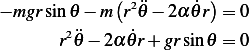

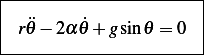
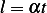 it will mean that the string
has been pulled all the way back to the pivot and
it will mean that the string
has been pulled all the way back to the pivot and 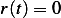 . So when running the solution it needs to run from
. So when running the solution it needs to run from
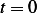 up to
up to 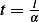 .
.
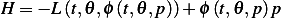
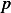 called the canonical momentum by
called the canonical momentum by
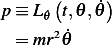
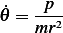
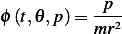
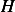
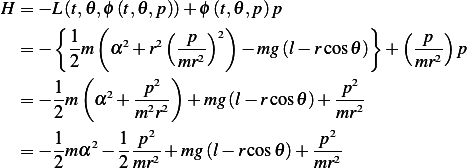
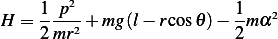
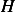 to the total energy. The total instantaneous energy of the system is
to the total energy. The total instantaneous energy of the system is
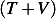 , hence we need to determine if
, hence we need to determine if 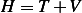 or not.
or not.
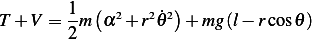
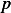 by
by 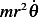 in (5) or replace
in (5) or replace 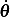 by
by 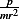 .
Lets do the later, hence
.
Lets do the later, hence 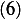 becomes
becomes
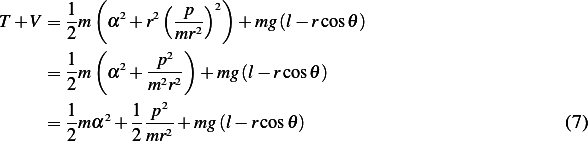
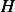 is the total energy, then (7)-(6) should come out to be zero, lets find out
is the total energy, then (7)-(6) should come out to be zero, lets find out
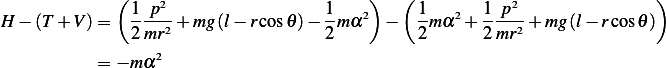
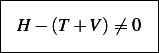
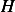 does not represents the total energy, and the
does not represents the total energy, and the

 slides down the rim of a circular hoop of radius
slides down the rim of a circular hoop of radius 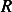 . The hoop stands vertically
and rotates about its diameter with angular velocity
. The hoop stands vertically
and rotates about its diameter with angular velocity 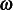 . Determine the equation of motion of the
bead.
. Determine the equation of motion of the
bead.
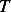 is made up of 2 components, one due to motion of the bead along the hoop itself
with speed
is made up of 2 components, one due to motion of the bead along the hoop itself
with speed 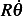 , and another due to motion with angular speed
, and another due to motion with angular speed 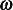 which has speed given by
which has speed given by
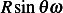
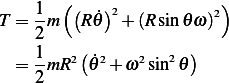
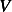 is due to the bead movement up and down the hoop, which is the standard
is due to the bead movement up and down the hoop, which is the standard 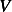 for a pendulum given
by
for a pendulum given
by