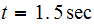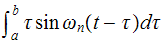 .
I derive it once.
.
I derive it once.
HW 3. CEE 247. Structural Dynamics. UCI. Fall 2006
Nasser Abbasi
Integration by parts is used in many problems below to solve
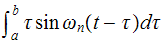 .
I derive it once.
.
I derive it once.
Let
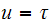 and
and
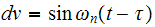 hence
hence
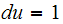 and
and
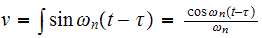
Hence
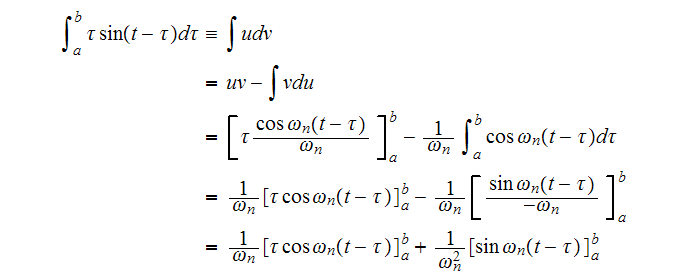
Hence the integral
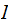 becomes
becomes
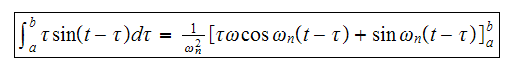
The above is the form to remember.
or
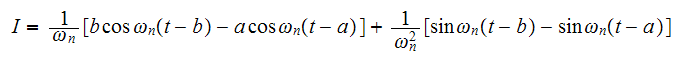
For example, when
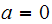 ,
,
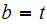 ,
we obtain
,
we obtain
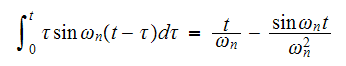
Solution
We first assume that the initial absolute state of the girder is
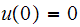 ,
and
,
and
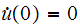
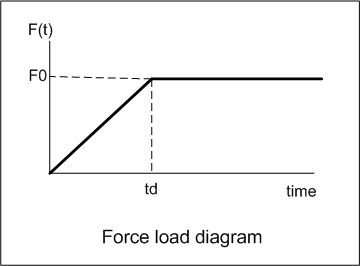
This is the force load diagram
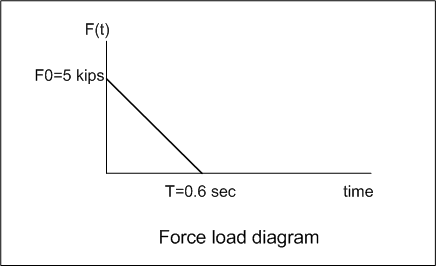
The intercept is
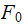 and the slope is
and the slope is
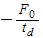 hence since the general line equation for
hence since the general line equation for
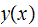 is
is
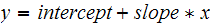 ,
we see that the equation for force loading is
,
we see that the equation for force loading is
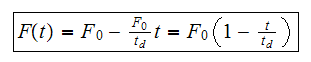
First we draw the physical model diagram
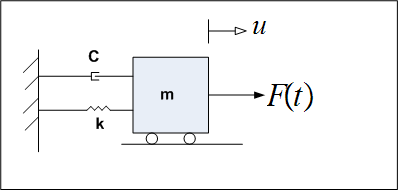
Using Duhamel integral, the displacement
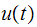 is (using the assumption of no damping)
is (using the assumption of no damping)
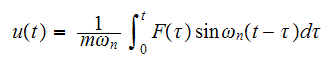
Substitute (1) into the above and carry the integration.
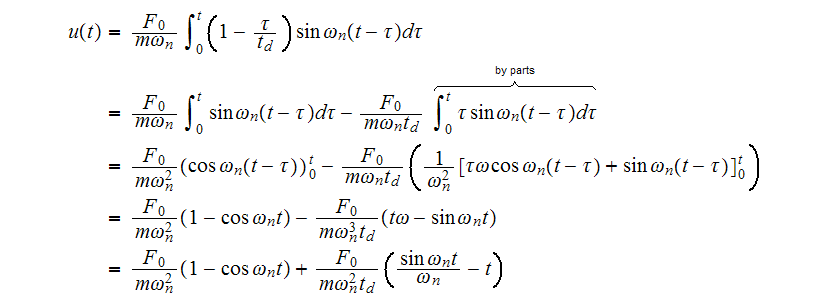
But
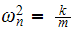 hence the above becomes
hence the above becomes
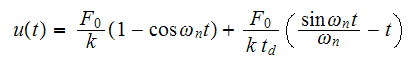
Now to find the stiffness

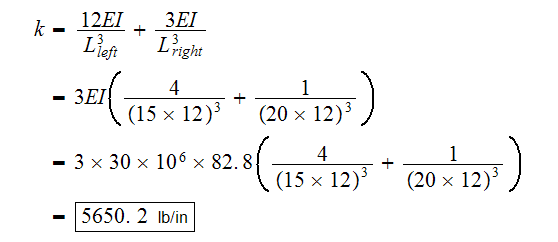
Hence
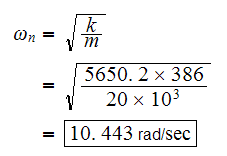
Now substitute the above results for
 and
and
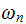 in equation (2), and evaluate at
in equation (2), and evaluate at
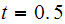 we obtain
we obtain
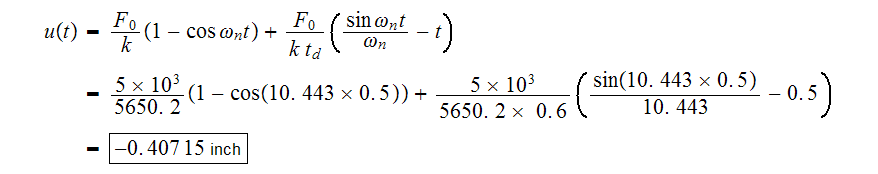
part(b)
To find maximum displacement
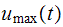 we use the response spectrum shown on page 107 of the 5th edition of the text
book. First we find the natural period
we use the response spectrum shown on page 107 of the 5th edition of the text
book. First we find the natural period
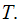
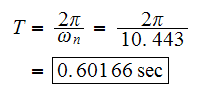
Hence
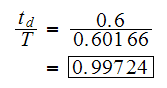
Hence from the spectrum on page 107, we see that
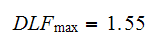 approximately
approximately
But
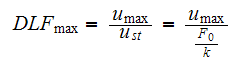
Hence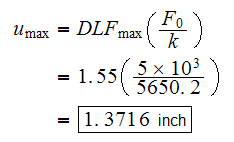
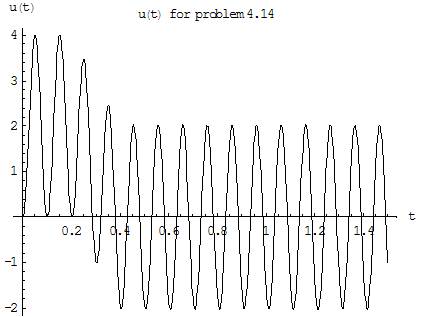
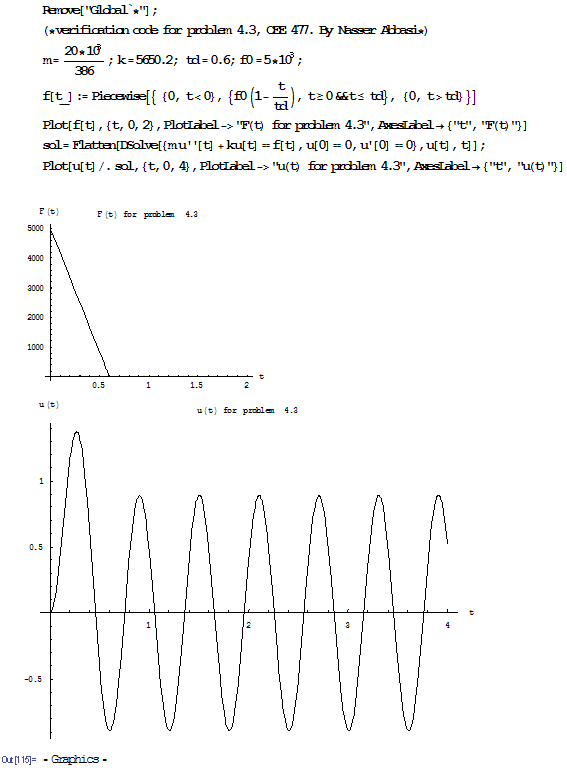
This is a small program to plot u(t) itself. We see that
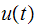 became maximum before
became maximum before
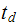 .
.
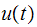 maximum as at about
maximum as at about
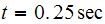
solution
fig P4.5 is
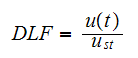
Hence we need to find
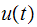
For
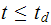 and for an undamped simple oscillator, using Duhamel integral, the
displacement
and for an undamped simple oscillator, using Duhamel integral, the
displacement
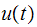 is
is
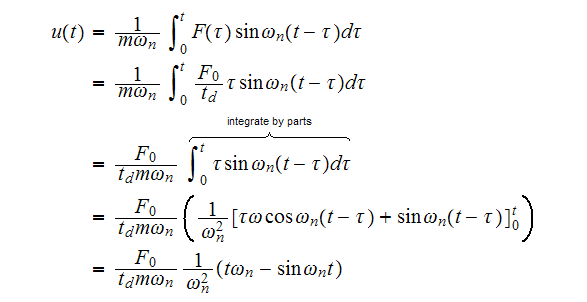
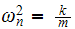 hence the above becomes
hence the above becomes
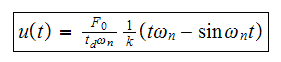
Now we find
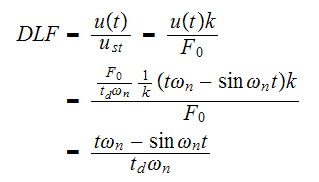
Hence
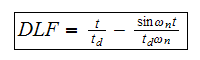
Now we do the case for
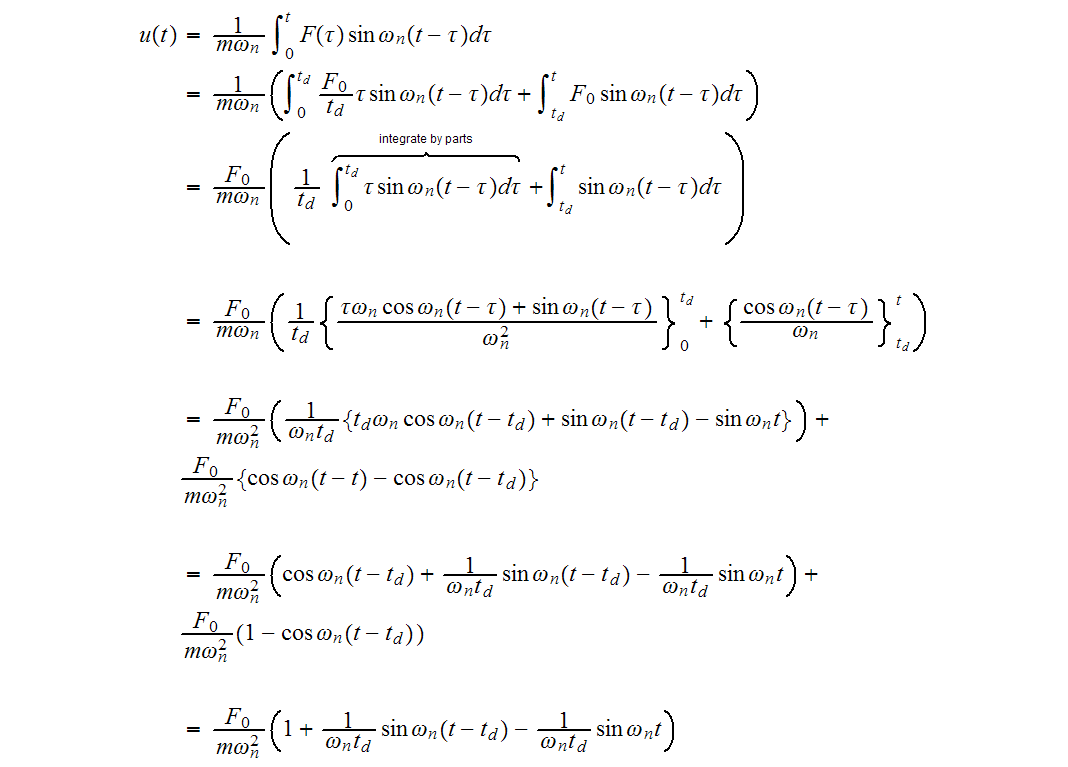
Hence
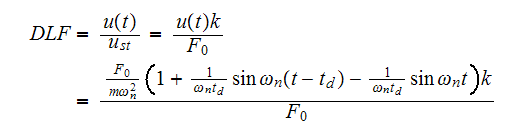
But
 hence the above becomes
hence the above becomes
Notice there is a sign difference with the answer on the back of the book. The back of the book gives
I think the answer in the back of the book is wrong. One way to obtain the
book answer from my answer is to replace
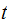 by
by
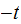 .
.
Frame shown in problem 4.3 above is subjected to sudden acceleration of 0.5 g applied to the foundation. Determine the maximum shear force in the columns. Neglect damping.
solution
The equation for motion when the system is subjected to ground acceleration can be written as
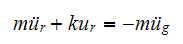
Where
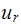 is the relative motion of the girder to the ground, and
is the relative motion of the girder to the ground, and
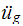 is the ground acceleration (absolute). Hence
is the ground acceleration (absolute). Hence
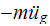 is the effective force
is the effective force

Hence this is the same problem as
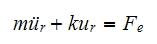
which has the solution
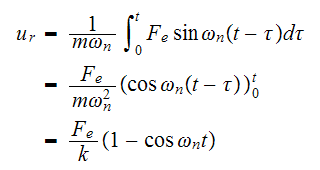
Hence
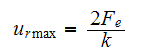
But from problem 4.3, we calculated
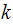 to be
to be
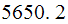 lb/in
lb/in hence
hence
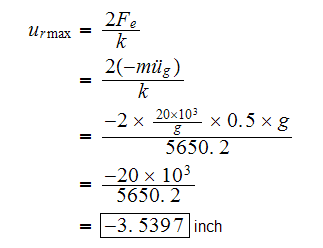
Now maximum shear is given by
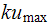 ,
hence for the left column we have (I will take absolute value of displacement,
since we are only interested in maximum value, the sense of shear is not
relevant).
,
hence for the left column we have (I will take absolute value of displacement,
since we are only interested in maximum value, the sense of shear is not
relevant).
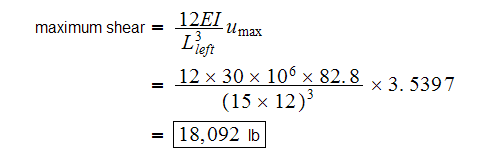
and for the right column
solution
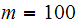 lb
lb
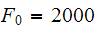 lb
lb
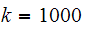 lb/in
lb/in
Let
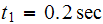
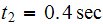
Hence for
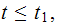
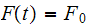
For
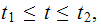
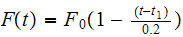
For an undamped simple oscillator, using Duhamel integral, the displacement
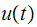 is
is
Hence for
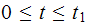
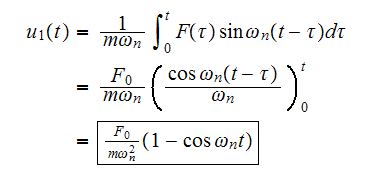
Hence
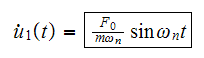
Note that
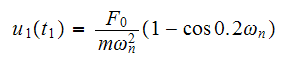 and
and
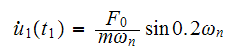
Now for
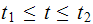
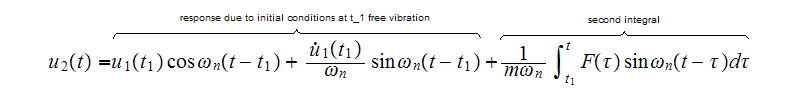
But the free vibration response is , using
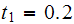
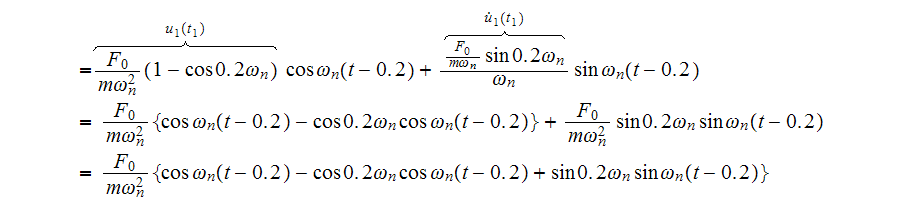
and the second integral is
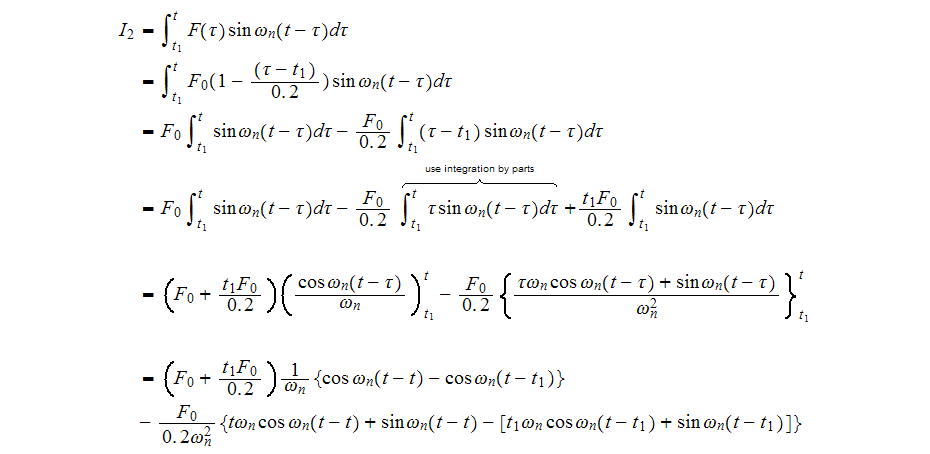
Simplify to
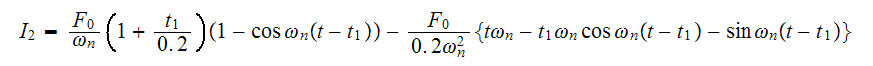
Hence
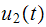 for
for
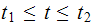 is by putting the above result back into (1) we obtain
is by putting the above result back into (1) we obtain
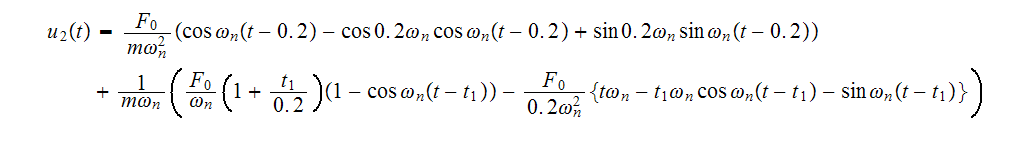
But
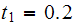 ,
hence
,
hence
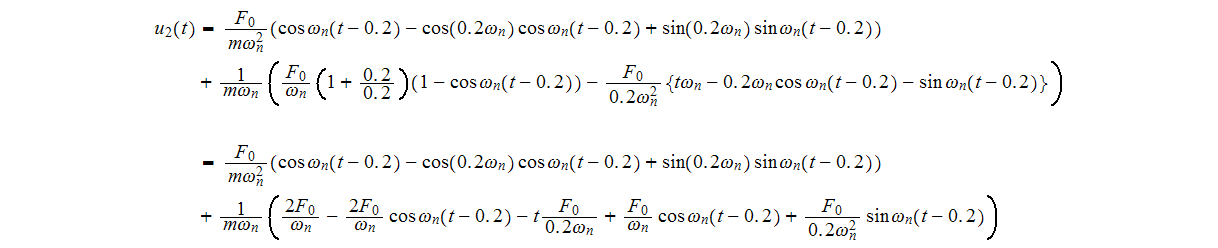
simplify
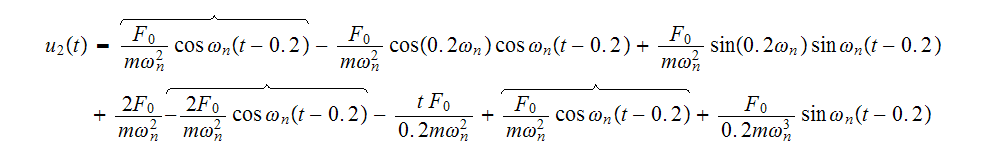
Hence
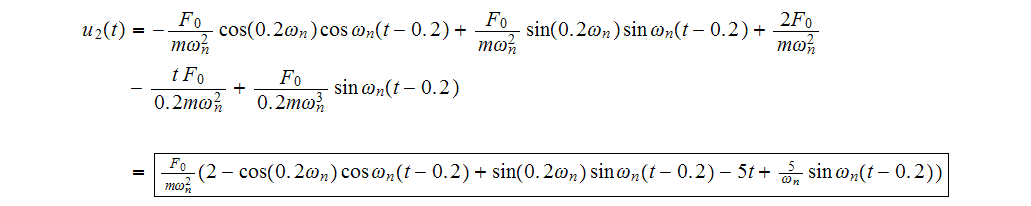
Now
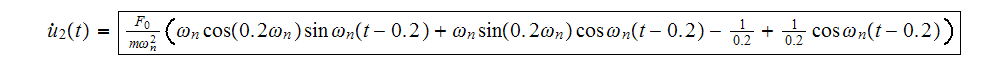
Note that at
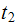 we have
we have
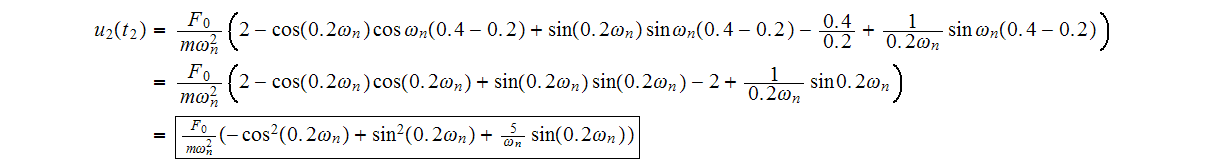
and at
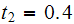 we have
we have
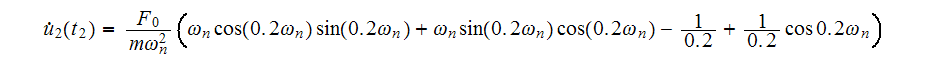
Now for
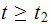 since no force is applied, we use the free vibration solution using the above
since no force is applied, we use the free vibration solution using the above
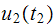 and
and
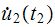 as initial conditions
as initial conditions
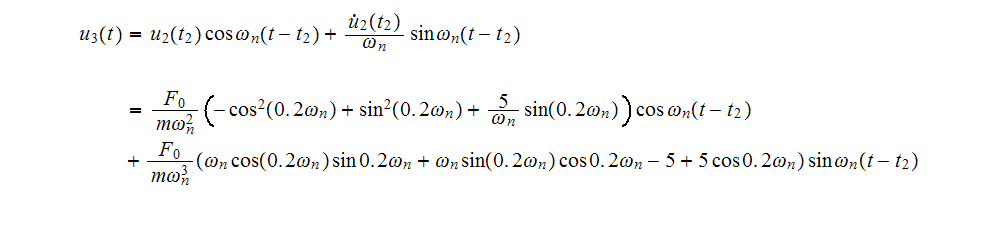
Now that we have
 for each time segment, we can plot the solution. Here it is for up to
for each time segment, we can plot the solution. Here it is for up to
 sec
sec
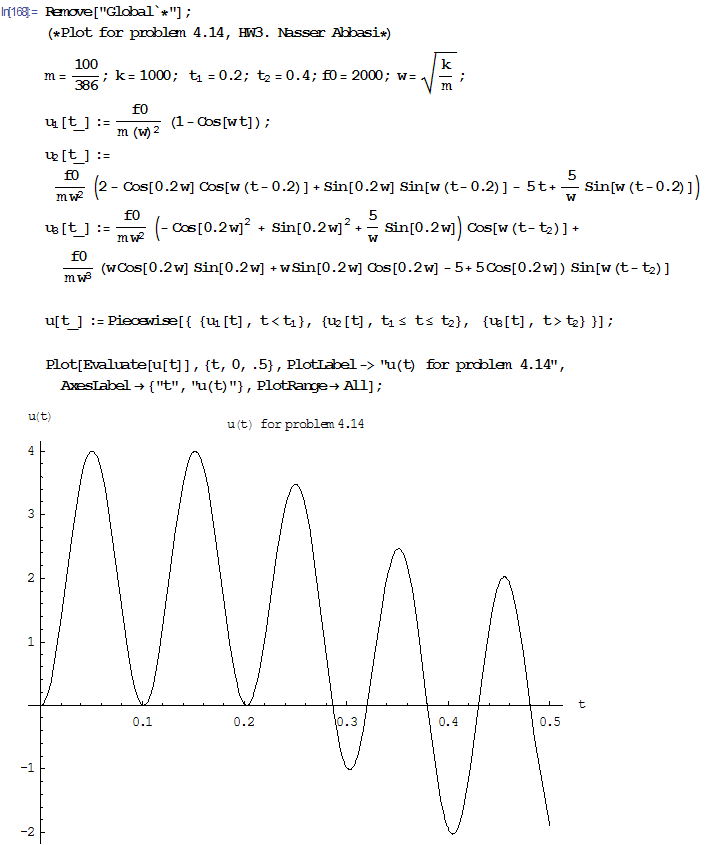
Here is the solution for up to