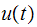 from a SDOF system with natural period of
from a SDOF system with natural period of
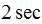 and
and
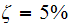 to the El Centro ground motion N-S component. Implement one of the numerical
time-stepping algorithms.
to the El Centro ground motion N-S component. Implement one of the numerical
time-stepping algorithms.
HW 4. CEE 247. Structural Dynamics. UCI. Fall 2006.
Nasser Abbasi
Determine and plot the deformation response
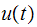 from a SDOF system with natural period of
from a SDOF system with natural period of
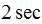 and
and
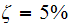 to the El Centro ground motion N-S component. Implement one of the numerical
time-stepping algorithms.
to the El Centro ground motion N-S component. Implement one of the numerical
time-stepping algorithms.
Derivation used was based on TextBook 'Structural Dynamics' 5th edition by Paz and Leigh. Page 185.
First, The El Centro data needed was downloaded from this web
site
http://nisee.berkeley.edu/data/
Here is listing of the first few lines of the file:
Data for El Centro 1940 North South Component (Peknold Version)
1559 points at equal spacing of 0.02 sec
Points are listed in the format of 8F10.5, i.e., 8 points across in
a row with 5 decimal places
The units are (g)
*** Begin data ***
0.00630 0.00364 0.00099 0.00428 0.00758 0.01087 0.00682 0.00277
-0.00128 0.00368 0.00864 0.01360 0.00727 0.00094 0.00420 0.00221
0.00021 0.00444 0.00867 0.01290 0.01713 -0.00343 -0.02400 -0.00992
0.00416 0.00528 0.01653 0.02779 0.03904 0.02449 0.00995 0.00961
0.00926 0.00892 -0.00486 -0.01864 -0.03242 -0.03365 -0.05723 -0.04534
We start by the equation of motion for SDOF system, using relative motion to
support subjected to suppose accelaration of
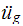
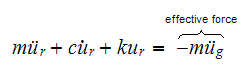
The ground accelaration
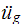 is given from the El-centro earthquake measurements.
is given from the El-centro earthquake measurements.
Solve using the method of linear acceleration. We start by writing the above equation as
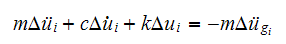
Where in the above all the mass displacement, velocity and acceleration are relative to the support and are not the absolute values.
Rewrite the above, to remove the unknown mass
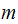 as follows
as follows
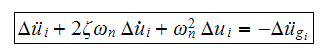
Following the analysis of the text book, from equation 6.36 on page 186, and
using
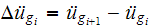 we have the following expression for the change of displacement at time step
we have the following expression for the change of displacement at time step
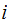
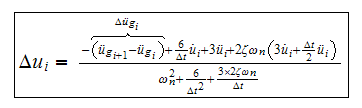
and hence we can now find
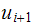 using
using
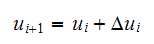
Now, we can find
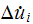 from equation 6.31 in the book
from equation 6.31 in the book
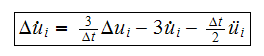
Hence
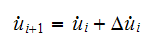
And
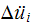 is obtained directly from equation (1) above
is obtained directly from equation (1) above
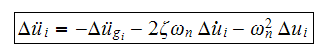
Hence
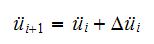
Now that
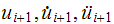 have been obtained, the process is repeated for the next step.
have been obtained, the process is repeated for the next step.
We start the process by using the initial conditions of
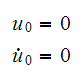
The El-centro data file gives the values of
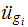 ,
which we will use to solve this problem.
,
which we will use to solve this problem.
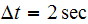 for this data.
for this data.
Hence the algorithm is as follows
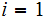 ,
,
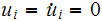
read
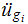 and
and
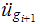 from El-centro file, and find
from El-centro file, and find
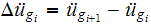
Find
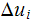 from eq (2). Find
from eq (2). Find
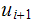 from eq (3)
from eq (3)
Find
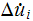 from eq (4). Find
from eq (4). Find
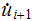 from eq (5)
from eq (5)
Find
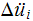 from eq (6). Find
from eq (6). Find
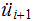 from eq (7)
from eq (7)
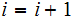 and go to step 2. Stop when
and go to step 2. Stop when
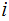 is the length of the el-centro data less than 1
is the length of the el-centro data less than 1
The following is a listing of the program and the output