HW 5. CEE 247. Structural Dynamics. UCI. Fall 2006.

Nasser Abbasi

Problem 7.1

Solution

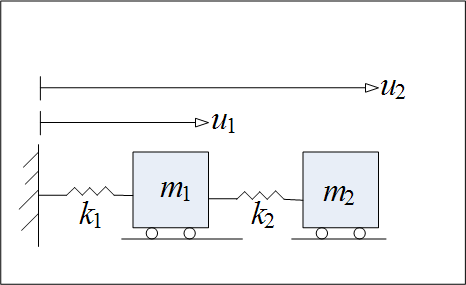
The idealized physical system is the following

The Lagrangian of the system is

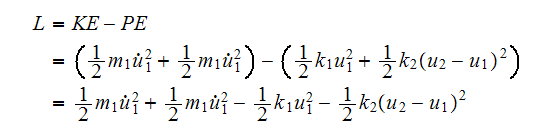
Now apply Euler equation on the Lagrangian to obtain the equation of motion for each degree of freedom. Given the equation of motion for is given by

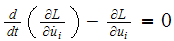
Hence the equation of motion associated with is given by

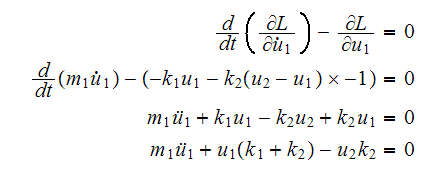
And the equation of motion associated with is given by

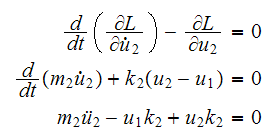
Hence the equation of motions are

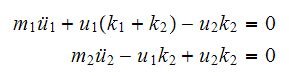
Hence the overall system EQM can be put in a matrix form as follows

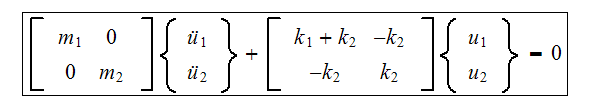
Notice that the mass matrix 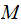and the stiffness matrix 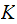are symmetric. This will always be the case for conservative systems.

Equation (3) can be written as

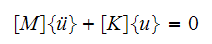
Now assume the solution is given by

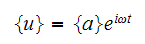
Substitute (5) into (4) we obtain

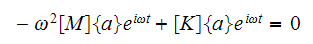
Since 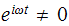we divide by it and obtain

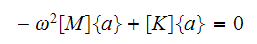
Factor out

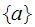
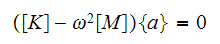
To have a non-trivial solution for the motion the above implies that the determinant of 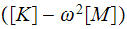must be zero. Hence we need to solve

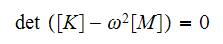
Let 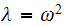, and expand the matrices and rewrite we obtain

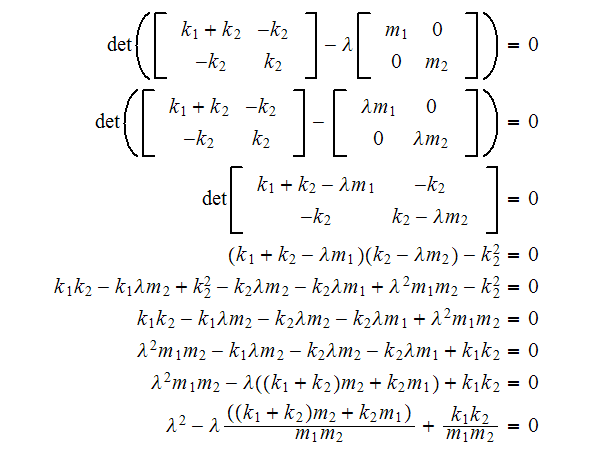
Now find the numerical values for 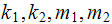and plug into the above equation to find

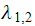
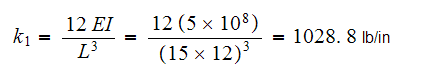
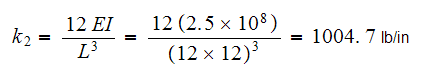
and

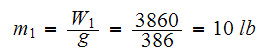
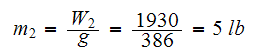
Hence eq (6) above becomes

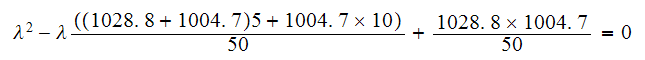
Hence

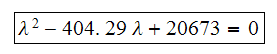
Hence this is now in standard quadratic format, solve for

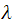
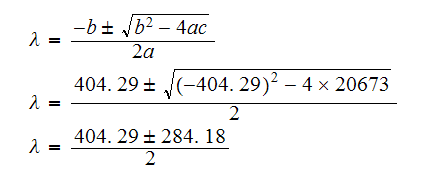
Hence

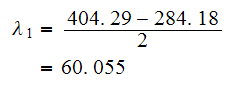
and

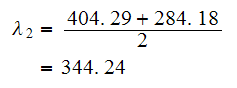
Since 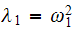then

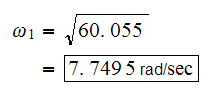
and similarly

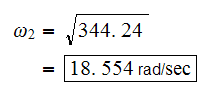
Now to find the eigenvectors, since

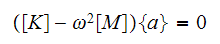
Then

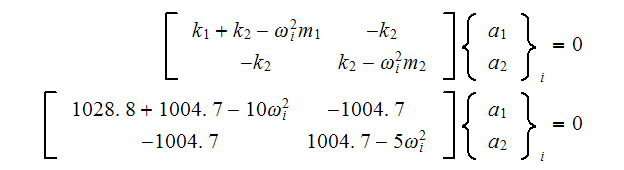
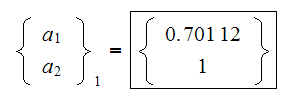
For the first eigenvalue 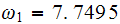the above becomes

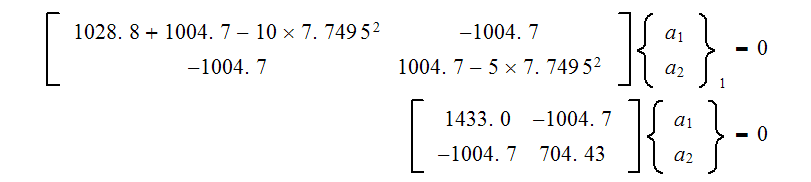
From first equation we obtain

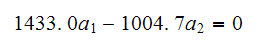
Hence

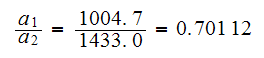
Hence we choose the first eigenvector to be

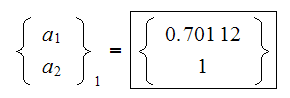
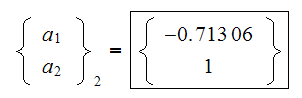
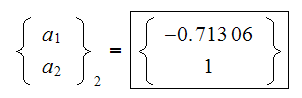
For the second eigenvalue

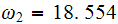
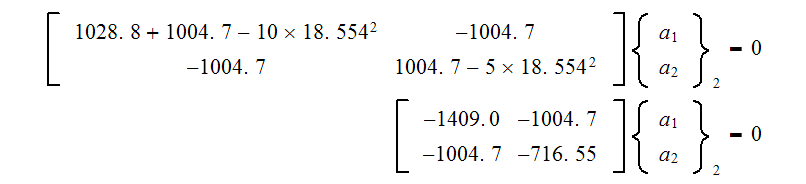
From first equation we obtain

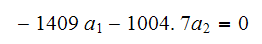
Hence

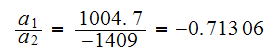
Hence we choose the second eigenvector to be

Conclusion

Problem 7.6

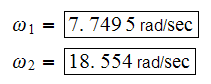
Answer

First deterrmine the stiffness and the masses.

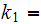
I wrote a Mathematica program to solve this. This is the result, and below that I attach step by step run of the program