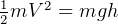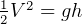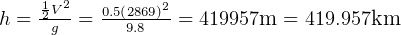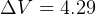 km/sec to transfer from LEO at inclination
km/sec to transfer from LEO at inclination 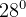 to GEO.
to GEO. 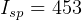 sec,
sec, 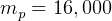 kg,
kg, 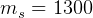 kg. How much payload can tug deliver to GEO? can tug make a
round trip without payload? if it can, how much payload could it carry to GEO and still return to
LEO?
kg. How much payload can tug deliver to GEO? can tug make a
round trip without payload? if it can, how much payload could it carry to GEO and still return to
LEO?
Problem: Given that total 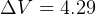 km/sec to transfer from LEO at inclination
km/sec to transfer from LEO at inclination 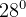 to GEO.
to GEO. 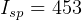 sec,
sec, 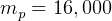 kg,
kg, 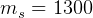 kg. How much payload can tug deliver to GEO? can tug make a
round trip without payload? if it can, how much payload could it carry to GEO and still return to
LEO?
kg. How much payload can tug deliver to GEO? can tug make a
round trip without payload? if it can, how much payload could it carry to GEO and still return to
LEO?
Assumptions
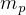 given is that starting from LEO, and not from surface of earth.
given is that starting from LEO, and not from surface of earth.
roundtrip is back to LEO, not earth.
Method
We are given 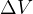 and asked to find payload that could be carried given the physical properties of the
spacecraft.
and asked to find payload that could be carried given the physical properties of the
spacecraft.
Solve from total 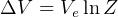
For the other parts of the problem, use the rocket equation again to solve for different variables as shown in the analysis.
Analysis
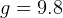 m/s.
m/s.
so 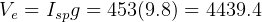 m/s
m/s
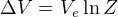
hence 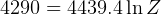
hence 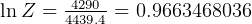
hence 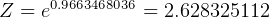
so 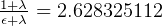
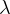 is the payload ratio
is the payload ratio
 is the structural ratio
is the structural ratio
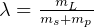
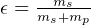
so 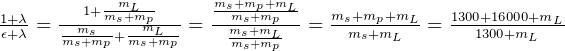
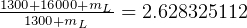
solve for 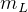
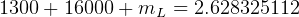
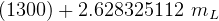
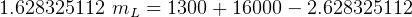
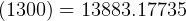
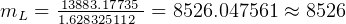 kg
kg
To find if tug can make a round-trip to LEO without payload, make 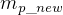 as the unknow, solve for it,
and compare it to the given
as the unknow, solve for it,
and compare it to the given 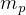 .
.
Now we have an aditional 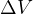 which is that needed to go back from GEO to LEO.
which is that needed to go back from GEO to LEO.
So, our 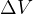 now is
now is 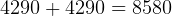 km/s
km/s
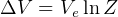
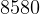
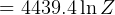
hence 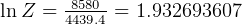
hence 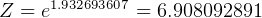
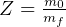
Here, 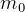 is the initial mass at start of the trip, which is
is the initial mass at start of the trip, which is 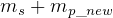 , and
, and 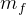 is the final mass at the
end of the trip, which now is
is the final mass at the
end of the trip, which now is 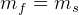
So, 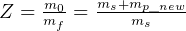 solve for
solve for 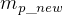 and compared to give
and compared to give 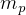 to see if less than.
to see if less than.
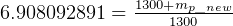
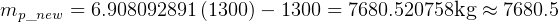 kg
kg
Compare this to the 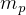 that the tug actually has which is
that the tug actually has which is 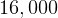 kg, so the answer is Yes, it can make a
round trip back to LEO with no payload.
kg, so the answer is Yes, it can make a
round trip back to LEO with no payload.
To find how much payload it can carry and still make a round trip to LEO. Since the 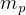 needed to make a round trip with NO payload was found above to be
needed to make a round trip with NO payload was found above to be 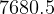 kg, then the
kg, then the 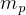 that we can use to make one second half of the round trip with no payload is
that we can use to make one second half of the round trip with no payload is 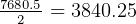 kg
kg
So, given that we started with 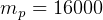 kg, then the
kg, then the 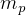 that we have at our disposal in the first half of
the trip is the difference
that we have at our disposal in the first half of
the trip is the difference 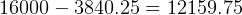 kg. This is the
kg. This is the 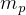 we can use for the one way trip from
LEO to GEO with a payload. We know find this payload.
we can use for the one way trip from
LEO to GEO with a payload. We know find this payload.
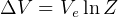
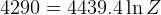
hence 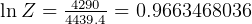
hence 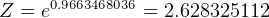
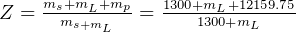 solve for
solve for 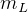
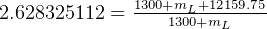
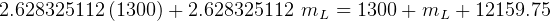
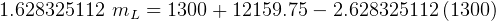
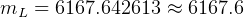 kg
kg
see problem on page 226, Weisel book.
Assumptions: burn-time is zero long. g (earth accelaration) does not change during the flight of the spacecraft.
Method: Use the rocket equation
Analysis
for the overall system
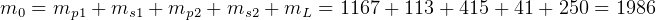 kg
kg
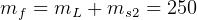
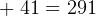 kg
kg
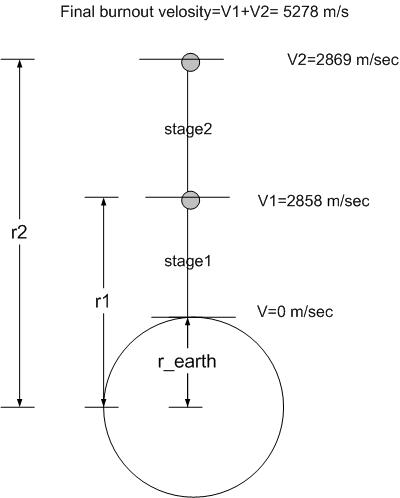
burn out for end of first stage:
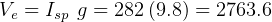 m/sec
m/sec
First stage:
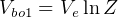
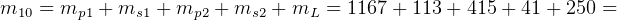
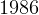 kg
kg
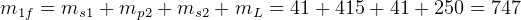 kg
kg
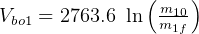
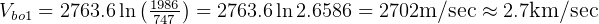
second stage:
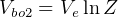
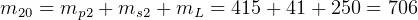 kg
kg
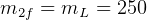 kg
kg
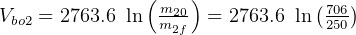
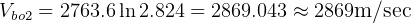
so, final burnout velosity is the sum of the above 2 velosities:
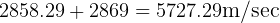
To find max altitude with 250 kg.
Find the mechanical energy 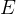 at surface of earth and at end of last stage, and use to solve for the
unknowns
at surface of earth and at end of last stage, and use to solve for the
unknowns 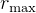 since
since 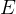 does not change over the path.
does not change over the path.
Convert 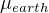 to m/sec, which is
to m/sec, which is
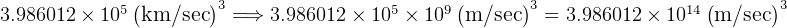
At surface of earth, and noting that the velosity of the rocket is zero at that point, we get
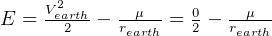
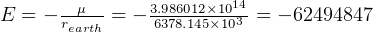 m
m /s
/s
now, final velosity is 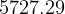 m/sec, so
m/sec, so
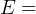
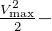
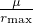
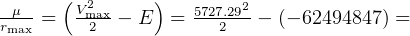
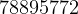
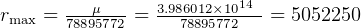 m
m
So, max altitude 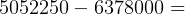
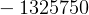 m
m 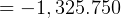 km
km
Not sure why I get negative ALT. I think this is because zero potential energy reference is usually taken at
 . This should then be
. This should then be
_________________________________max alt = 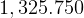 km
km
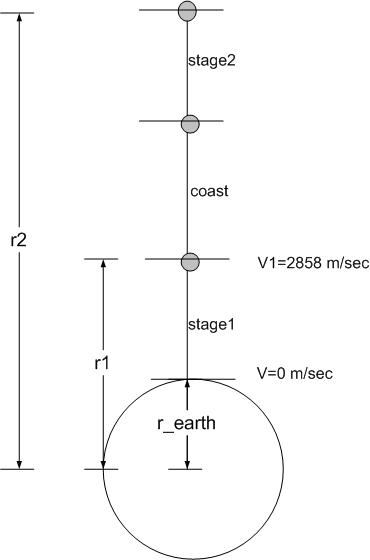
At end of stage 1 we know the velocity. Let the spacecraft coast from that point untill its velosity becomes zero. Then start stage2.
At end of stage one, the mass of spacecraft is 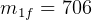 kg.
kg.
The K.E. the spacecraft have at this point is 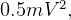 then at end of coast, this K.E. will all be exchanged
by P.E. gained in going up, so solve for distance travelled
then at end of coast, this K.E. will all be exchanged
by P.E. gained in going up, so solve for distance travelled
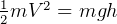
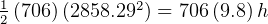
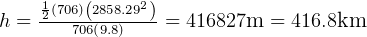
Now, the spacecraft fires its second stage rocket, at end of the second stage it will have gained a velosity of
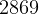 m/sec (found from above). Mass of spacecraft at end of stage 2 is
m/sec (found from above). Mass of spacecraft at end of stage 2 is 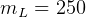 kg
kg
From