MAE 185. Numerical Methods for Mechanical Engineers. Spring 2003.

UCI.

Student Name: Nasser Abbasi

Assignment #1.

Problems

5.3 Determine the real roots of

f(x)=-26+82.3x –88x^2 +45.4 x^3 –9x^4 +0.65 x^5

(b) Using bisection to determine the highest root to E_s=10%. Employ and initial guesses of X_l=0.5 and X_u=1.0

6.9 Determine the lowest positive root of f(x)=7 sin(x) exp(-x) –1

(b) Using the Newton-Raphson method (three iterations, x_i=0.3)

6.11 Determine the roots of the following simulataneous nonlinear equations using (a) fixed-point iteration and (b) the Newton-Raphson method:

x = y+x^2 – 0.5

y = x^2 – 5xy

Employee initial guesses of x=y=1.0 and discuss the results.

7.5 Use Bairstow’s method to determine the roots of

(c)f(x)=x^4 - 2x^3 + 6x^3 - 2x +5

Solutions

5.3 part (b)

Using bisection method.

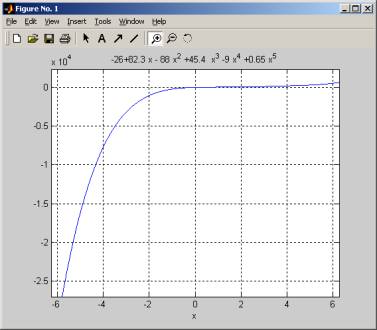
Before starting, plot the function to get an idea of where the root is located.

>> ezplot('-26+82.3*x - 88*x^2 +45.4* x^3 -9*x^4 +0.65*x^5')

This table below shows the progress of the iterations.

In this table, x1 is the ‘lower’ point, and x2 is the ‘upper’ point.

x_m is the middle point. It is found from (x2-x1)/2.

Start with x1=0.5 and x2=1.0 as given in the problem.

At each iteration the size of the region containing the root decreases by a factor of 2. Assume the size of the original region containing the root is A, and assume that the desired size of the ending tolerance is B, hence the number of iterations is log2(A/B). In this problem A=0.5 and B=(10% A). This is below a graphical representation of bisection.

‘x’ below represents where the root being bracketed is.

ß----------A=0.5 ------à

|-------------x----------| 100%

|-----x----------| 50%

|-----x--| 25%

|-x--| 12.5%

|-x| 6.25%

<-->

Hence the number of iterations needed to reach a region 10% of the original region is log2(0.5/(0.10*0.5))= log2(1/0.1)=log2(10)= 3.322 or 4 iterations.

E_s is the ratio of the size of the new bracketing region to the original size of the bracketing region as a percentage.

Iter	x1	x_m	x2	f(x1)	f(x_m)	f(x2)	Max Err	Es %
1	0.5	0.75	1.0	-1.7171875	2.684717	5.35	0.5	50
2	0.5	0.625	0.75	-1.7171875	0.8351822	2.684717	0.25	25
3	0.5	0.5625	0.625	-1.7171875	-0.334188	0.8351822	0.125	12.5
4	0.5625	0.59375	0.625	-0.334188	0.2747303	0.835182	0.0625	6.25

So we take x=0.59375 as the approximation to the root.

Solution to 5.3 (c)

Here, use the requla falsi formula of

x2 = x1 – f(x1)*(x0-x1)/( f(x0) – f(x1) )

(see page 44 of the main text book for how the above formula was derived)

f(x)=-26+82.3x –88x^2 +45.4 x^3 –9x^4 +0.65 x^5

start with x0=0.5, x1=1.0

Using the algorithm shown on table 47 of the text book:

REPEAT

Set x2= x1 – f(x1)*(x0-x1)/( f(x0) – f(x1) )

IF f(x2) of opposite sign to f(x0)

Set x1=x2

ELSE

Set x0=x2

END IF

UNTIL | f(x2) | < tolerance

In this problem we are asked to stop when E_s=0.1%, where

The difference between this method and the bisection method is that the size of the new bracketing region is not neccessarly half the size of the bracketing region of the previous step. Hence we do not know in advance the number of steps needed to achieve the required tolerance.

To know when to stop use this: when the delta change of the size of the bracketed region is 0.1% of the size of the bracketed region of the previous step, then we stop. So, let s(i) be the size of the bracketed

Region at step i, then E_S = s(i-1)-s(i)/(s(i-1) * 100 %

	x0	x1	F(x0)	f(x1)	X2	Size of region	E_s
1	0.5	1.0	-1.7171875	0.7745010	0.621490	1.0-0.5 =0.5
2	0.5	0.62149	-1.7171875	0.0849378	0.583727	0.621490-0.5 =0.12149	0.5-0.12149/0.5 = 75.7%
3	0.5	0.583727	-1.7171875	0.0088116	0.579781	0.583727-0.5 =0.083727	0.12149-0.083727/0.12149 =31.08%
4	0.5	0.579781	-1.7171875	0.0009087	0.579373	0.579781-0.5 =0.079781	0.083727-0.079781/0.083727 =4.71%
5	0.5	0.579373	-1.7171875	0.0009010	0.579331	-.579373-0.5 =0.079373	0.079781-0.079373/0.079781 =0.51%
6	0.5	0.579331	-1.7171875	9.285377E-005	0.57932671	0.579331-0.5 =0.079331	0.079373- 0.079331/0.079373 =0.05%

So root is taken as 0.57932671

To verify, I used matlab symbolic solve function to find the real root:

>> solve('-26+82.3*x - 88*x^2 +45.4* x^3 -9*x^4 +0.65*x^5')

ans =

[ .579326592861950261846454370632]

[ 1.07726983544428433169938136893-.860621514282949848638960605085*i]

[ 1.07726983544428433169938136893+.860621514282949848638960605085*i]

[ 5.55614379120166361430046836883-2.33378449456931739881421919764*i]

[ 5.55614379120166361430046836883+2.33378449456931739881421919764*i]

This shows there is one real root which is .579326592861950261846454370632.

So the false position method converged to the actual root faster than the bisection method did after the same number of iterations. This is the expected result for functions that are smooth near the root.

Solution to 6.9 (b)

Using Newton-Raphson method.

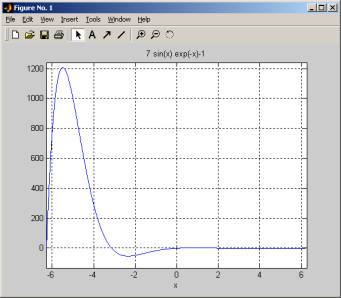
Before starting, plot the function to get an idea of where the roots are

This is a plot of f(x)=7 sin(x) exp(-x) –1

The iteration formula is

x_(n+1) = x_n – f(x_n)/f’(x_n)

where f(x) = 7 sin(x) exp(-x) –1

so, f’(x) = 7 cos(x) exp(-x) – 7 sin(x) exp(-x)

This table shows the 3 iterations. We start with x=0.3 (I assumed the first step is not part of the iteration process)

n	x_n	f(x_n)	f’(x_n)	x_(n+1)
0	0.3	0.5324873	3.4216275	0.144376
1	0.144376	-0.1282708	5.1241684	0.1694085
2	0.1694085	-0.0037214	4.8282779	0.1701793
3	0.1701793	-0.0000035	4.8193032	0.170179994

So, after 3 iteration, we take x=0.170179994 as approximation to the root

To verify, used matlab to solve it

>> solve('7*sin(x)*exp(-x)-1')

ans =

.170179993753835176860864670115239502017737590738214599312052

Solution for 6.9 (c)

Using the secant method. Start with x1=0.4, x0=0.5

F(x1)= 0.8272

F(x0)= 1.0355

Since |f(x0)| > |f(x1)| then no need to swap x0 with x1.

(i.e. need to keep x1 closer to the root)

Using the iteration formula given in the book on page 44

x2= x1 – f(x1)*(x0-x1)/( f(x0) – f(x1) )

x0= x1

x1= x2

The result of the calculation is shown in this table

N	X0	X1	F(x0)	F(x1)	X2
0	0.5	0.4	1.0355040	0.827244	0.002782
1	0.4	0.002782	0.8272444	-0.9805797	0.218237
2	0.002782	0.218237	0.2184109	-0.9805801	0.178990
3	0.218237	0.178989	0.2184127	0.0420032	0.169644

So, after 3 iterations, root is taken as 0.169644

This shows that Newton-Raphson method converged faster than the secant method to the root for this function.

Solution for 6.11 (a)

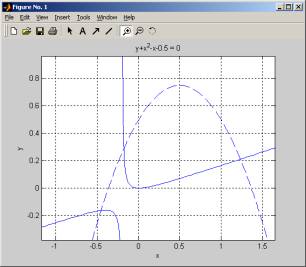
First I plot the 2 function to get an idea where the solutions are. The solution is where the 2 functions intersect.

ezplot('x^2-y-5*x*y');

hold on;

ezplot('y+x^2-x-0.5')

h=findobj(gca,'type','line');

set(h(1),'LineStyle','--')

So, I see that there are 3 solutions.

Zoom in:

let me also find the exact solutions using matlab to make sure my worked out answers are correct:

>> SOL=solve('x^2-y-5*x*y','y+x^2-x-0.5')

SOL =

x: [3x1 sym]

y: [3x1 sym]

>> SOL.x

ans =

[ -.45518959344844446505992693519646]

[ -.17812819955522914530391522665854]

[ 1.2333177930036736103638421618550]

>> SOL.y

ans =

[ -.16238715943220462132849109792298]

[ .29014214496798331801721391559981]

[ .21224501446422130331127718232317]

Now, using fixed point iteration to solve

x = y + x^2 – 0.5 ------ (1)

y = x^2 – 5xy ------ (2)

let x=g(x,y), y=f(x,y). Start iteration with x=1, y=1.

With g(x,y)=y+x^2 – 0.5, and f(x,y)=x^2 –5xy we get this table

X	y	x=G(x,y)	Y=F(x,y)
1	1	1.5	-4
1.5	-4	-2.25	32.25
-2.25	32.25	36.8125	367.875

So, x and y values are diverging. Forms selected for g(x) and f(y) are not working. I Need to select different form.

Rewrite (1) as y=x-x^2+0.5 ---- (1)

Rewrite (2) as x=(x^2-y)/5y ---- (2)

Now, y=G(x,y) = x - x^2 + 0.5

X=f(x,y) = (x^2-y) / 5y

Start with x=y=1, I get this table

X	y	y=G(x,y)	X=F(y,x)
1	1	0.5	0
0	0.5	0.5	-0.2
-.2	.5	.34	-.216
-.216	.34	.330656	-.1533
-.1533	.330656	.3702	-.1765
-.1765	.3702	.29235	-.1688
-.1688	.29235	.30271	-.17151
-.17151	.30271	.299	-.1705

This form seems to converge to around y=.29 and x=-0.17

So one solution is y=0.29 and x=-0.17

This agrees with matlab. This finds one solution.