Problem 18.5

Nasser Abbasi, MAE 185. UCI. April 24, 2003.

Given data

X	1	2	3	5	6
F(x)	4.75	4	5.25	19.75	36

Calculate f(4) using Newton’s interpolating polynomial or order 1 through 4.

Solution:

Set up the forward divided-difference table.

First I set it in symbolic form, then plug in the values.

x0	F0	F1-f0 F[x0,x1]= ------ X1-x0	F[x1,x2] – F[x0,x1] F[x0,x1,x2]= ------------------ X2 – x0	F[x1,x2,x3] – F[x0,x1,x2] F[x0,x1,x2,x3]= --------------------- X3 – x0	F[x1,x2,x3,x4] – F[x0,x1,x2,x3] F[x0,x1,x2,x3,x4]= -------------------------- X4 – x0
x1	F1	F2-F1 F[x1,x2]= ----- X2-x1	F[x2,x3] – F[x1,x2] F[x1,x2,x3]= ------------------ X3 – x1	F[x2,x3,x4] – F[x1,x2,x3] F[x1,x2,x3,x4]= --------------------- X4 – x1
x2	F2	F3-f2 F[x2,x3]= ----- X3-x2	F[x3,x4] – F[x2,x3] F[x2,x3,x4]= ------------------ X4 – x2
x3	F3	F4-f3 F[x3,x4]= ------ X4-X3
x4	F4

Now plug in the values for the observation points xi, fi, into the above table to get:

1	4.75	4-4.75 -------- = -0.75 2-1	1.25 – (-0.75) --------------- = 1 3 - 1	2 – 1 ---------- = 0.25 5 - 1	0.25 – 0.25 ----------------- = 0 6 - 1
2	4	5.25 - 4 --------- =1.25 3 - 2	7.25 – 1.25 ------------ = 2 5 - 2	3 - 2 ---------- = 0.25 6 - 2
3	5.25	19.75–5.25 ----------= 7.25 5-3	16.25 – 7.25 -------------- = 3 6 - 3
5	19.75	36–19.75 -------- = 16.25 6-5
6	36

So,

a0 = 4.75

a1 = -0.75

a2 = 1

a3 = 0.25

a4 = 0

So, Newton polynomial of order 1 is:

F(x) = a0 + a1 (x-x0)

F(x) = 4.75 – 0.75 (x-1) = 5.5 – 0.75 x

so

F(4) = 5.5 – 0.75 (4) = 2.5

Newton polynomial of order 2 is:

F(x) = the order one polynomial + a2 (x-x0)(x-x1)

F(x) = 5.5 – 0.75 x + (x-1)(x-2)

F(x) = 7.5 – 3.75 x + x^2

so

F(4) = 8.5

Newton polynomial of order 3 is:

F(x) = the order two polynomial + a3 (x-x0)(x-x1)(x-x2)

F(x) = 7.5 – 3.75 x + x^2 + 0.25 (x-1)(x-2)(x-3)

F(x) = 6 – x – 0.5 x^2 + 0.25 x^3

so

F(4) = 10;

So, Newton polynomial of order 4 is:

F(x) = the order 3 polynomial + a4 (x-x0)(x-x1)(x-x2)(x-x3)

F(x) = 6 – x – 0.5 x^2 + 0.25 x^3 + a4 (x-x0)(x-x1)(x-x2)(x-x3)

However, a4 = 0 . So this case is the same as the last case. Nothing to do.

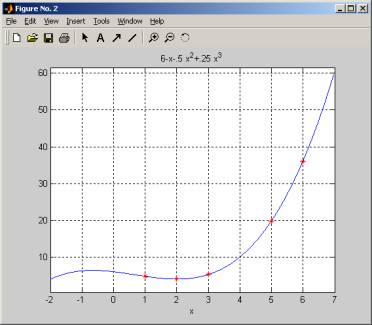
Now, Plot it to make sure the observation points are on the interpolation polynomial

>> ezplot('6-x-.5*x^2+.25*x^3',[-2,7]);

>> grid

>> hold on;

>> plot(1,4.75,'*r'); plot(2,4,'*r'); plot(3,5.25,'*r'); plot(5,19.75,'*r'); plot(6,36,'*r');

>>