This below builds
the A matrix:
>> r1=[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0];
>> r2=[8 4 2 1 0 0 0 0 0 0 0 0 0 0 0 0];
>> r3=[12 4 1 0 -12 -4 -1 0 0 0
0 0 0 0 0
0];
>> r4=[0
0 0 0 27 6 1
0 -27 -6 -1 0 0
0 0 0];
>> r5=[0 0 0 0 8 4 2 1 0
0 0 0 0 0 0
0];
>> r6=[0 0 0 0 27 9 3 1 0 0 0
0 0
0 0 0];
>> r7=[0
0 0 0 0 0 0
0 75 10 1 0 -75 -10 -1 0];
>> r8=[12 2 0 0 -12 -2 0 0 0
0 0 0 0 0 0
0];
>> r9=[0 0 0 0 0 0 0 0 27
9 3 1 0 0 0
0];
>> r10=[0 0 0 0 0 0 0 0 125
25 5 1 0 0
0 0];
>> r11=[0
0 0 0 18 2 0
0 -18
-2 0 0 0 0
0 0];
>> r12=[0
0 0 0 0 0 0
0 30
2 0 0 -30 2 0 0];
>> r13=[0 0 0 0 0 0 0 0 0
0 0 0 125 25 5 1];
>> r14=[0 0 0 0 0 0 0 0 0
0 0 0 216 36
6 1];
>> r15=[6
2 0 0 0 0 0
0 0
0 0 0 0 0 0
0];
>> r16=[0
0 0 0 0 0 0
0 0
0 0 0 36 2 0
0];
>> b=[4.75 4
0 0 4 5.25 0
0 5.25 19.75
0 0 19.74 36 0 0]';
>>
A=[r1;r2;r3;r4;r5;r6;r7;r8;r9;r10;r11;r12;r13;r14;r15;r16]
A =
1 1
1 1 0 0 0
0 0 0 0 0
0 0 0 0
8 4
2 1 0 0 0
0 0 0 0 0
0 0 0 0
12 4
1 0 -12 -4 -1
0 0 0 0 0
0 0 0 0
0 0
0 0 27 6 1
0 -27 -6 -1 0
0 0 0 0
0
0 0 0 8 4
2 1 0 0 0
0 0 0 0 0
0 0
0 0 27 9 3
1 0 0 0 0
0 0 0 0
0 0
0 0 0 0 0
0 75 10 1
0 -75 -10 -1 0
12 2
0 0 -12 -2 0
0 0 0 0 0
0 0 0 0
0 0
0 0 0 0 0
0 27 9 3 1
0 0 0 0
0 0
0 0 0 0 0
0 125 25 5 1
0 0 0 0
0 0
0 0 18 2 0
0 -18 -2 0 0
0 0 0 0
0 0
0 0 0 0 0
0 30 2 0 0
-30 2 0 0
0 0
0 0 0 0 0
0 0 0 0 0
125 25 5
1
0 0
0 0 0 0 0
0 0 0 0 0
216 36 6
1
6 2
0 0 0 0 0
0 0 0 0
0 0 0 0 0
0 0
0 0 0 0 0
0 0 0 0 0
36 2 0
0
>> b
b =
4.75
4
0
0
4
5.25
0
0
5.25
19.75
0
0
19.74
36
0
0
Now solve to find the spline parameters
>> x=inv(A)*b
x =
0.458506329113927
-1.37551898734178
0.167012658227857
5.49999999999999
-0.292531645569624
3.13070886075953
-8.84544303797469
11.5083037974684
1.05342405063291
-8.98289240506331
27.4953607594937
-24.8325000000001
0.206620253164557
-3.71916455696204
38.3683670886077
-104.950253164557
so, the above gives me the a1,b1,c1,d1,c2,
etc
the first element in x above is a1, the second is
b1, the third is c1, etc
so the 4 cubic splines are:
f1(x) =
0.4585 x^3 - 1.3755189 x^2 + 0.167 x + 5.49999999
f2(x) =
-0.29253 x^3 + 3.1307088 x^2 - 8.84544 x + 11.508303
f3(x) =
1.053424 x^3 - 8.982892
x^2 + 27.4953 x -
24.8325
f4(x) =
0.20662 x^3 - 3.7191645 x^2 + 38.36837 x - 104.950253
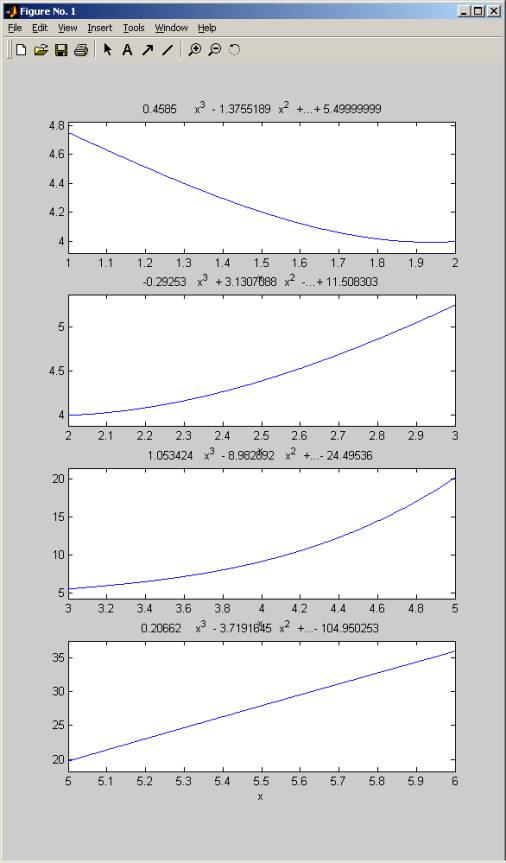
This is below a plot of each spline over its own
range:
>> subplot(4,1,1);
>> ezplot(' 0.4585 * x^3 - 1.3755189
*x^2 + 0.167* x + 5.49999999',[1 2]);
>> subplot(4,1,2); ezplot('-0.29253 * x^3 + 3.1307088 *x^2 - 8.84544 * x +
11.508303',[2 3]);
>> subplot(4,1,3); ezplot('1.053424 * x^3 - 8.982892 * x^2 + 27.4953 * x -
24.49536',[3 5]);
>> subplot(4,1,4); ezplot('0.20662 * x^3
- 3.7191645* x^2 + 38.36837*
x - 104.950253',[5 6]);
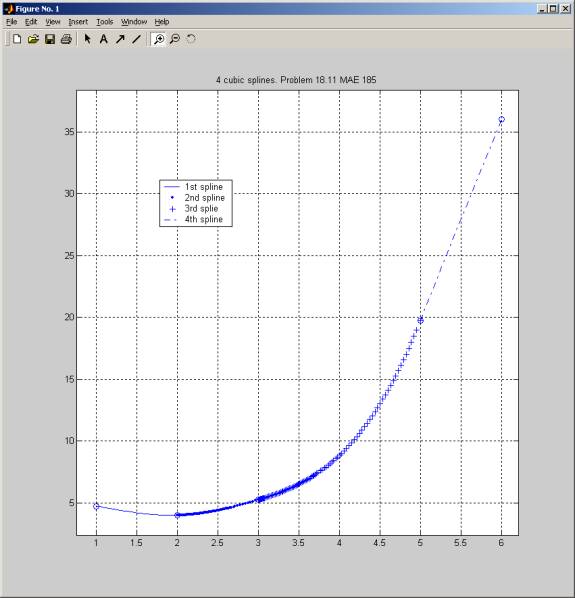
This below are the 4 splines when connected
togother.
f1(x) =
0.4585 x^3 - 1.3755189 x^2 + 0.167 x + 5.49999999
f2(x) =
-0.29253 x^3 + 3.1307088 x^2 - 8.84544 x + 11.508303
f3(x) =
1.053424 x^3 - 8.982892
x^2 + 27.4953 x -
24.8325
f4(x) =
0.20662 x^3 - 3.7191645 x^2 + 38.36837 x - 104.950253
fplot(inline('0.4585 * x^3 - 1.3755189
*x^2 + 0.167* x + 5.49999999'),[1 2],'-');
hold on;
fplot(inline('-0.29253 * x^3 + 3.1307088 *x^2 - 8.84544 * x +
11.508303'),[2 3],'.');
fplot(inline('
1.053424 * x^3 - 8.982892 *
x^2 + 27.4953 * x - 24.8325'),[3 5],'+');
fplot(inline(' 0.20662 * x^3 - 3.7191645*
x^2 + 38.36837* x - 104.950253'),[5 6],'-.');
axis([0 6.5 0 40]);
legend('1st
spline','2nd spline','3rd splie','4th spline');
grid
plot(1,4.74,'o'); plot(2,4,'o'); plot(3,5.25,'o');
plot(5,19.75,'o'); plot(6,36,'o');
title('4 cubic splines. Problem 18.11 MAE 185');
part (A)
To predict f(4):
Since x=4 is in the
range of spline 3, Ill use this spline:
f3(x) =
1.053424 x^3 - 8.982892
x^2 + 27.4953 x -
24.8325
>> x=4; eval('1.053424 * x^3 - 8.982892 * x^2 + 27.4953 * x -
24.8325');
8.841564
to predict f(2.5);
since 2.5 is in the range of second spline, use
f2(x) =
-0.29253 x^3 + 3.1307088 x^2 - 8.84544 x + 11.508303
plug x=2.5 in the above, I get: 4.39085175
part b)
plug in x=3 in the second spline equation, I get
f2(3) = 5.2500522
plug in x=3 in the third spline equation, I get:
f3(3) = 5.24982
They are almost the same as expected. (if I have
taken f2 = f3 at the shared point
between these splines, the difference should become even smaller).