|
x |
Y |
x^2 |
x^3 |
x^4 |
xY |
x^2 Y |
|
2 3 4 7 8 9 5 5 |
9 6 5 10 9 11 2 3 |
4 9 16 49 64 81 25 25 |
8 27 64 343 512 729 125 125 |
16
81
256
2401
4096
6561
625
625 |
18 18 20 70 72 99 10 15 |
36 54 80 490 576 891 50 75 |
|
43 |
55 |
273 |
1933 |
14661 |
322 |
2252 |
N=8
So equations are
8 a0
+ a1 (43) + a2 (273) = 55
43
a0 + a1
(273) + a2 (1933) =
322
273 a0
+ a1 (1933) + a2 (14661) = 2252
To solve for a0,a1,a2, I used MATLAB.
A=
8 43
273
43
273 1933
273 1933
14661
x= [a0 a1 a2]’
b= [55 322 2252]
Ax=b;
Solve for x.
>> A=[8 43 273; 43 273 1933; 273 1933 14661]
A =
8 43 273
43 273 1933
273 1933 14661
>> b=[55;322;2252]
b =
55
322
2252
>> x=inv(A)*b
x =
16.0269614835947
-4.80691868758908
0.488944365192578
so polynomial regression fit in least squares is
16.0269614835947
-4.80691868758908 x +
0.488944365192578 x^2
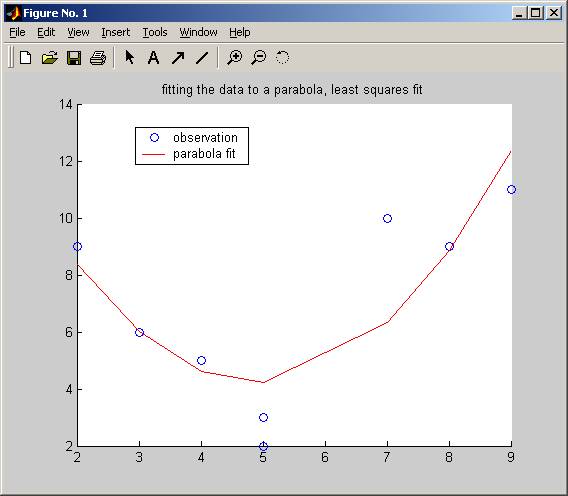
The above is the plot of the fitted parabola to the
data.
Now I need to compute the error.
|
x |
Y |
Fitted y |
e=Y-y |
e^2 |
|
2 3 4 7 8 9 5 5 |
9 6 5 10 9 11 2 3 |
8.3689015691869
6.00670470756071
4.62239657631969
6.33680456490755
8.86405135520715
12.3691868758919
4.21597717546382
4.21597717546382 |
-0.6310984308131
0.00670470756070962
-0.37760342368031
-3.66319543509245
-0.135948644792849
1.3691868758919
2.21597717546382
1.21597717546382 |
0.398285229374758
4.49531034746368e-005
0.142584345575092
13.4190007956822
0.0184820340210123
1.87467270111462
4.91055484217661
1.47860049124897 |
|
|
|
|
|
22.2422253922967 |
So, using a parabola, the error (in least squares sense) is 22.2422, compared to 62.26268 when fitting a stright line.
So error using parabola fitting is about 30% of the
error using a stright line. (all errors in least squares sense).