Results and output:

>> nma_RK4('y*(x^2-1.2)',0.25,0,2.0,1)

step x y(x) end_step_y

1 0.0000 1.0000 0.7447

2 0.2500 0.7447 0.5722

3 0.5000 0.5722 0.4680

4 0.7500 0.4680 0.4204

5 1.0000 0.4204 0.4279

6 1.2500 0.4279 0.5092

7 1.5000 0.5092 0.7308

8 1.7500 0.7308 1.3050

9 2.0000 1.3050 1.3050

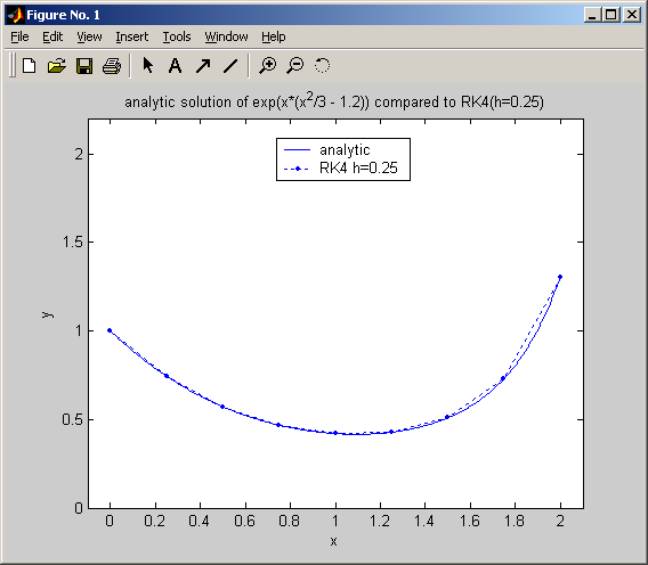
>> nma_RK4('y*(x^2-1.2)',0.5,0,2.0,1)

step x y(x) end_step_y

1 0.0000 1.0000 0.5723

2 0.5000 0.5723 0.4204

3 1.0000 0.4204 0.5091

4 1.5000 0.5091 1.2986

5 2.0000 1.2986 1.2986

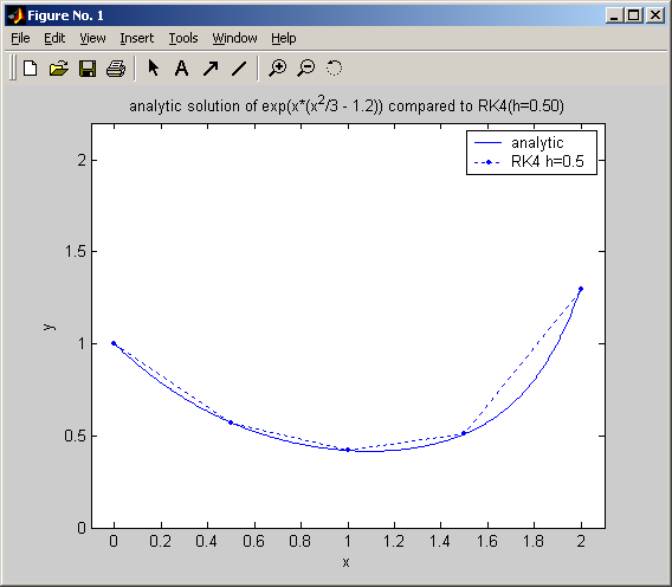
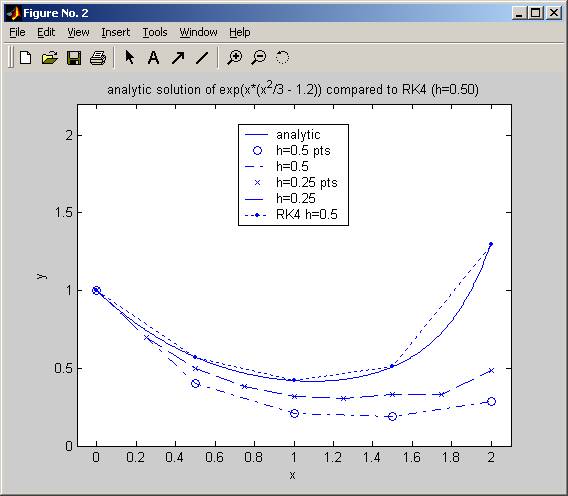
Comparing RK4 to Euler:

function nma_RK4(rate,stepSize,startX,endX,initialY)

%function nma_RK4(rate,stepSize,initialX,finalX)

% Function to solve ODE using Runge-Kutta classical 4th order

%INPUT

% rate: A string that represents the derivative dy/dx. This

% is the function f(x,y) in the ODE equation dy/dx= f(x,y)

% This string MUST use the letters 'x' and 'y' for the

% independent and the dependent variables respectively.

% For an example, in the equation dy/dx = y*x, the rate

% string is passed in as 'y*x'

% stepSize: This is 'h', the step size over x

% startX: The starting value of x

% endX: The ending value of x

% initialY: Initial condition. The value of y at startX.

% Author: Nasser Abbasi

FALSE = 0;

TRUE = 1;

y = initialY;

x = startX;

nStep = 0;

nPoints = (endX-startX)/stepSize +1;

currentPoint = 1;

while(currentPoint < nPoints)

startStepX = x;

endStepX = x + stepSize;

startStepY = y;

k1 = yder( rate, startStepX , startStepY );

k2 = yder( rate, startStepX+stepSize/2 , startStepY + (1/2)*stepSize*k1 );

k3 = yder( rate, startStepX+stepSize/2 , startStepY + (1/2)*stepSize*k2 );

k4 = yder( rate, startStepX+stepSize , startStepY + stepSize*k3 );

nStep = nStep+1;

data(nStep,1) = nStep;

data(nStep,2) = startStepX;

data(nStep,3) = startStepY;

y = startStepY + stepSize * ( (1/6) * (k1+ 2*k2+ 2*k3+ k4) );

data(nStep,4) = y;

currentPoint = currentPoint+1;

x = x + stepSize;

end

nStep = nStep+1;

data(nStep,1) = nStep;

data(nStep,2) = x;

data(nStep,3) = y;

data(nStep,4) = y;

analyze(data,stepSize);

%%%%%%%%%%%%%%%%%%%%

function dydx=yder(f,x,y)

dydx=eval(f);

%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%

function analyze(d,stepSize)

[row,col]=size(d);

fprintf('step\t x\t\t y(x) \t end_step_y\n');

N=0;

for(i=1:row)

fprintf('%d\t %7.4f\t %7.4f\t %7.4f\n',...

d(i,1),d(i,2),d(i,3),d(i,4));

end

plotAnalyticAndRKOnly(d,stepSize);

figure;

x_5=[0 0.5 1 1.5 2];

y_5=[1 0.4 0.21 0.189 0.288225];

x_25=[0 0.25 0.5 0.75 1 1.25 1.5 1.75 2];

y_25=[1 0.7 0.5009375 0.38196484375 0.321089196777344 ...

0.305034736938477 0.332678509973526 0.332678509973526 0.487581941179949];

y_analytic='exp(x*(x^2/3 - 1.2))';

ezplot(y_analytic,0,2);

hold on;

plot(x_5,y_5,'o')

plot(x_5,y_5,'-.')

plot(x_25,y_25,'x')

plot(x_25,y_25,'--')

plot(d(:,2),d(:,3),'.:')

xlim([-0.1 2.1]);

ylim([0 2.2])

legend('analytic','h=0.5 pts','h=0.5','h=0.25 pts','h=0.25','RK4 h=0.5');

ylabel('y');

title(sprintf('analytic solution of %s compared to RK4 (h=%.2f)',y_analytic,stepSize));

%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%

function plotAnalyticAndRKOnly(cleanData,stepSize)