HOME

PDF (letter size)

Solve

$$\begin{array}{rl}\text{(1)}& \frac{\partial u}{\partial t}& =k\frac{{\partial }^{2}u}{\partial x^2}0& <x<L\\ t& >0\end{array}$$

Initial conditions

$$u(0,x)=0$$

Boundary conditions

$$\begin{array}{rl}u(0,t)& =\sin \left(t\right)\\ u(t,L)& =0\end{array}$$

Let $$\begin{array}{}\text{(2)}& u=v+u_E\end{array}$$ where $u_E(x,t)$ is steady state solution that only needs to satisfy boundary conditions and $v(x,t)$ satisfies the PDE itself but with homogenous B.C.  At steady state, the PDE becomes

$$\begin{array}{rl}0& =k\frac{d^2{u}_E}{d{x}^2}\\ u_E\left(0\right)& =\sin \left(t\right)\\ u_E\left(L\right)& =0\end{array}$$

The solution is $u_E\left(t\right)=\left(\frac{L-x}{L}\right)\sin \left(t\right)$.  Hence (2) becomes

$$u(x,t)=v(x,t)+\left(\frac{L-x}{L}\right)\sin \left(t\right)$$

Substituting the above in (1) gives

$$\begin{array}{rl}\frac{\partial v}{\partial t}+\left(\frac{L-x}{L}\right)\cos \left(t\right)& =k\frac{{\partial }^{2}v}{\partial x^2}\\ \frac{\partial v}{\partial t}& =k\frac{{\partial }^{2}v}{\partial x^2}+\left(\frac{x-L}{L}\right)\cos \left(t\right)\\ \text{(3)}& \frac{\partial v}{\partial t}& =k\frac{{\partial }^{2}v}{\partial x^2}+Q(x,t)\end{array}$$

With boundary conditions $u_0(0,t)=0,u(L,t)=0$. This is now in standard form and separation of variables can be used to solve it. $$Q(x,t)=\left(\frac{x-L}{L}\right)\cos \left(t\right)$$ Now acts as a source term. The eigenfunctions are known to be ${\mathrm{\Phi }}_n\left(x\right)=\sin \left(\sqrt{{\lambda }_n}x\right)$ where ${\lambda }_n={\left(\frac{n\pi }{L}\right)}^2$. Hence by eigenfunction expansion, the solution to (3) is

$$\begin{array}{}\text{(3A)}& v(x,t)=\sum _{n=1}^{\mathrm{\infty }}{B}_n\left(t\right){\mathrm{\Phi }}_n\left(x\right)\end{array}$$

Substituting this into (3) gives

$$\begin{array}{}\text{(4)}& \sum _{n=1}^{\mathrm{\infty }}\frac{d{B}_n\left(t\right)}{dt}{\mathrm{\Phi }}_n\left(x\right)=k\sum _{n=1}^{\mathrm{\infty }}{B}_n\left(t\right){\mathrm{\Phi }}_n^{\prime \prime }\left(x\right)+Q(x,t)\end{array}$$

Expanding $Q(x,t)$ using same basis (eigenfunctions) gives

$$Q(x,t)=\sum _{n=1}^{\mathrm{\infty }}{q}_n\left(t\right){\mathrm{\Phi }}_n\left(x\right)$$

Applying orthogonality

$$\begin{array}{rl}{\int }_0^{L}Q(x,t){\mathrm{\Phi }}_m\left(x\right)dx& ={\int }_0^L\sum _{n=1}^{\mathrm{\infty }}{q}_n\left(t\right){\mathrm{\Phi }}_n\left(x\right){\mathrm{\Phi }}_m\left(x\right)dx\\ & =\sum _{n=1}^{\mathrm{\infty }}{q}_n\left(t\right){\int }_0^L{\mathrm{\Phi }}_n\left(x\right){\mathrm{\Phi }}_m\left(x\right)dx\end{array}$$

But $\sum _{n=1}^{\mathrm{\infty }}{\int }_0^L{\mathrm{\Phi }}_n\left(x\right){\mathrm{\Phi }}_m\left(x\right)dx={\int }_0^L{\mathrm{\Phi }}_m^2\left(x\right)dx=\frac{L}{2}$ since ${\mathrm{\Phi }}_n\left(x\right)=\sin \left(\frac{n\pi }{L}x\right)$ and the above simplifies to

$$\begin{array}{rl}{\int }_0^{L}Q(x,t){\mathrm{\Phi }}_n\left(x\right)dx& =\frac{L}{2}{q}_n\left(t\right)\\ q_n\left(t\right)& =\frac{2}{L}{\int }_0^{L}Q(x,t)\sin \left(\frac{n\pi }{L}x\right)dx\end{array}$$

But $Q(x,t)=\left(\frac{x-L}{L}\right)\cos \left(t\right)$, hence

$$\begin{array}{rl}{q}_n\left(t\right)& =\frac{2}{L}{\int }_0^L\left(\frac{x-L}{L}\right)\cos \left(t\right)\sin \left(\frac{n\pi }{L}x\right)dx\\ & =\frac{-2}{n\pi }\cos \left(t\right)\end{array}$$

Therefore $Q(x,t)=\sum _{n=1}^{\mathrm{\infty }}{q}_n\left(t\right){\mathrm{\Phi }}_n\left(x\right)=\sum _{n=1}^{\mathrm{\infty }}\frac{-2}{n\pi }\cos \left(t\right)\sin \left(\frac{n\pi }{L}x\right)$ and (4) becomes

$$\begin{array}{rl}\sum _{n=1}^{\mathrm{\infty }}\frac{d{B}_n\left(t\right)}{dt}{\mathrm{\Phi }}_n\left(x\right)& =k\sum _{n=1}^{\mathrm{\infty }}{B}_n\left(t\right){\mathrm{\Phi }}_n^{\prime \prime }\left(x\right)-\sum _{n=1}^{\mathrm{\infty }}\frac{2}{n\pi }\cos \left(t\right)\sin \left(\frac{n\pi }{L}x\right)\\ \frac{d{B}_n\left(t\right)}{dt}\sin \left(\frac{n\pi }{L}x\right)& =k{B}_n\left(t\right)(-\frac{n^2{\pi }^2}{L^2}\sin \left(\frac{n\pi }{L}x\right))-\frac{2}{n\pi }\cos \left(t\right)\sin \left(\frac{n\pi }{L}x\right)\\ \frac{d{B}_n\left(t\right)}{dt}+B_n\left(t\right)k\frac{n^2{\pi }^2}{L^2}& =-\frac{2}{n\pi }\cos \left(t\right)\end{array}$$

This is an ODE in $B_n\left(t\right)$ whose solution is

$$B_n\left(t\right)=C_n{e}^{-k\left(\frac{n^2{\pi }^2}{L^2}\right)t}-\frac{2L^2(k{n}^2{\pi }^2\cos t+L^2\sin t)}{n\pi (L^4+k^2{n}^4{\pi }^4)}$$

From (3A) $v(x,t)$ now becomes

$$\begin{array}{}\text{(5)}& v(x,t)=\sum _{n=1}^{\mathrm{\infty }}{C}_n{e}^{-k\left(\frac{n^2{\pi }^2}{L^2}\right)t}\sin \left(\frac{n\pi }{L}x\right)-\frac{2L^2(k{n}^2{\pi }^2\cos t+L^2\sin t)}{n\pi (L^4+k^2{n}^4{\pi }^4)}\sin \left(\frac{n\pi }{L}x\right)\end{array}$$

To find $C_n$, from initial conditions, at $t=0$ the above becomes

$$0=\sum _{n=1}^{\mathrm{\infty }}{C}_n\sin \left(\frac{n\pi }{L}x\right)-\frac{2L^2\left(k{n}^2{\pi }^2\right)}{n\pi (L^4+k^2{n}^4{\pi }^4)}\sin \left(\frac{n\pi }{L}x\right)$$

Hence

$$C_n=\frac{2L^2\left(k{n}^2{\pi }^2\right)}{n\pi (L^4+k^2{n}^4{\pi }^4)}$$

Therefore (5) becomes

$$v(x,t)=\sum _{n=1}^{\mathrm{\infty }}(\frac{2L^2\left(k{n}^2{\pi }^2\right)}{n\pi (L^4+k^2{n}^4{\pi }^4)}{e}^{-k\left(\frac{n^2{\pi }^2}{L^2}\right)t}-\frac{2L^2(k{n}^2{\pi }^2\cos t+L^2\sin t)}{n\pi (L^4+k^2{n}^4{\pi }^4)})\sin \left(\frac{n\pi }{L}x\right)$$

And since $u=v+u_E$ then the solution is

$$u(x,t)=(\sum _{n=1}^{\mathrm{\infty }}(\frac{2L^2\left(k{n}^2{\pi }^2\right)}{n\pi (L^4+k^2{n}^4{\pi }^4)}{e}^{-k\left(\frac{n^2{\pi }^2}{L^2}\right)t}-\frac{2L^2(k{n}^2{\pi }^2\cos t+L^2\sin t)}{n\pi (L^4+k^2{n}^4{\pi }^4)})\sin \left(\frac{n\pi }{L}x\right))+\left(\frac{L-x}{L}\right)\sin \left(t\right)$$

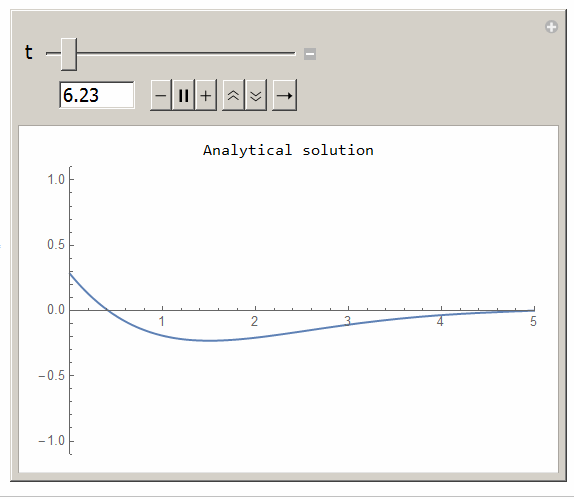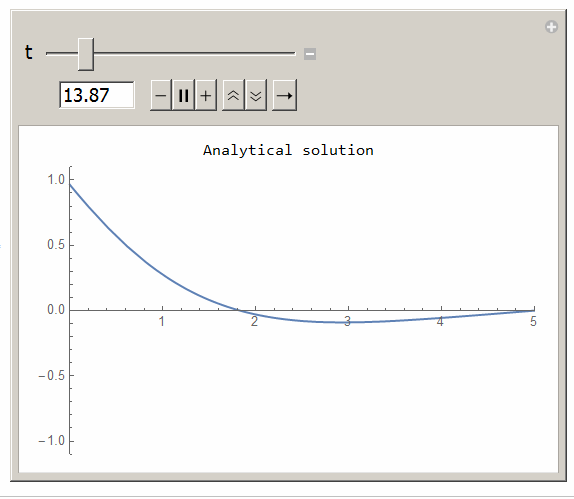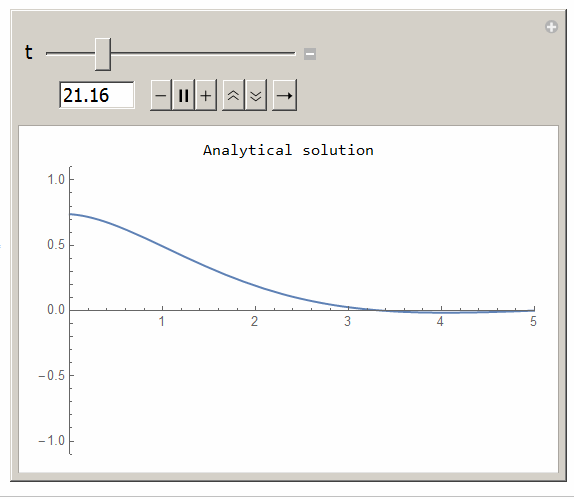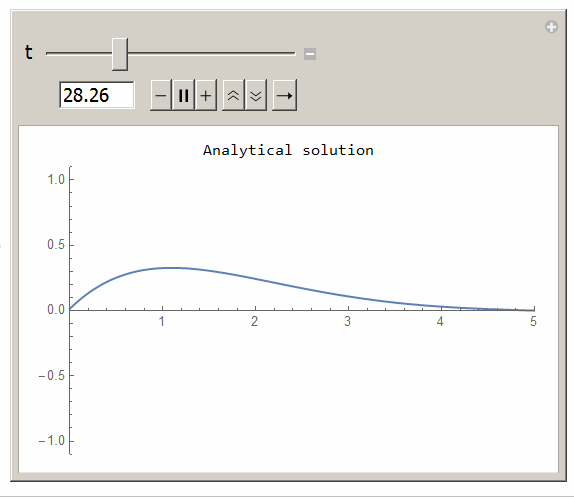
To simulate

ClearAll[t, x, n] 
k = 1; L0 = 5; max = 400; 
u[x_, t_] = 
Sum[(((2*L0^2*(k*n^2*Pi^2))/(n*Pi*(L0^4 + k^2*n^4*Pi^4)))* 
      Exp[(-k)*((n^2*Pi^2)/L0^2)*t] - 
      (2*L0^2*(k*n^2*Pi^2*Cos[t] + L0^2*Sin[t]))/(n* 
      Pi*(L0^4 + k^2*Pi^4*n^4)))*Sin[((n*Pi)/L0)*x], 
      {n, 1, max}] + ((L0 - x)/L0)*Sin[t]; 
 
Manipulate[Grid[{{"Analytical solution"}, 
     {Plot[Evaluate[u[x,t]],{x,0,5},PlotRange->{{0,5},{-1.1,1.1}}, 
     ImageSize->400]}}], 
     {{t,0,"t"},0,100,.01} 
]
 

Here is the animation from the above

start  stop

Here is the numerical solution to compare with

ClearAll["Global`*"]; 
pdeset = {Derivative[1, 0][U][t, x] == Derivative[0, 2][U][t, x]} 
ics = {U[0, x] == 0}; 
bcs = {U[t, 0] == Sin[t], U[t, 5] == 0}; 
ibcAll = {ics, bcs}; 
 
numericalSol = NDSolve[{pdeset, ibcAll}, U, {t, 0, 100}, {x, 0, 5}]; 
 
Manipulate[Grid[{{"Numerical solution"}, 
       {Plot[Evaluate[U[t, x] /. numericalSol], {x, 0, 5}, 
       PlotRange -> {{0, 5}, {-1, 1}}, ImageSize -> 400]}}], 
       {{t, 0, "t"}, 0, 100, .01} 
]
 

Here is the animation from the above

start  stop

Reference: stokes second problem question and answer