Basic relations. Let f(x) be a PDF for some continuous random variable. Then the following is true
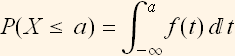
As can be verified as follows (using Normal distribution as an example) by evaluating the above integral and see if it the same as CDF(X=a)
Using Mathematica to study basic probability
by Nasser Abbasi, september 30, 2007
Basic relations. Let f(x) be a PDF for some continuous random variable. Then the following is true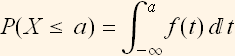
As can be verified as follows (using Normal distribution as an example) by evaluating the above integral and see if it the same as CDF(X=a)
In[1]:=

Out[3]=
![]()
Now find F (a), it should be the same as above
![]()
![]()
Another important relation is probability of X being in some range. This is the same as the area under the curve of f(x) between the 2 points:
The above is found as follows

![]()
Now find F (b)-F(a), it should be the same as above

![]()
![]()
lets try to see how to find probabilty of X be in some range when X is discrete. Assume X is a discrete random variable, say a Binomial. We need to do the same as above. Now we can not use Integrate, but need to us SUM

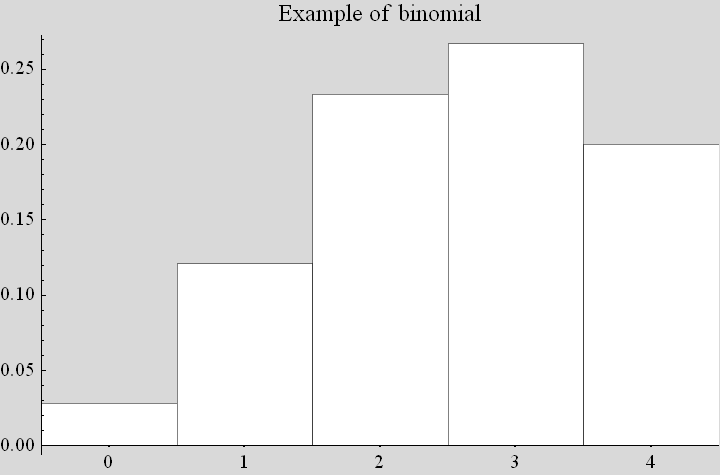
Let find P (X < 3) in the above. Now instead of integration, we use sum, we want to add the area under the PDF from 0 to 3. But the width is 1 for each interval. So we just sum the y values.
![]()
![]()
Verify by checking the CDF at 3, it should be the same as above
![]()
![]()
To show that probability mass function adds to one. Say we have binomial distribution
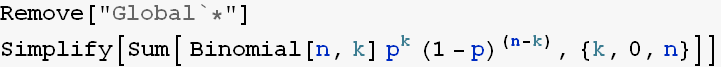

![]()
![]()
| Created by Wolfram Mathematica 6.0 for Students - Personal Use Only (29 December 2007) |