Test notebook for my Mathematica package
![]()
![]()
![]()
![]()
copyright Nasser M. Abbasi
Last updated Jan 10, 2017
This notebook tests each function on nma.m, which is package I maintain that contains some useful functions.
![]()
![]()
![]()

butterd
![]()

butterworth digital filter design
test1

![]()
![]()
![]()
![]()
![]()
test2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
butterToBandPass
![]()

test1
make a normalized butter low pass analog filter of order 4

![]()
convert to band pass

![]()
Plot the magnitude spectrums


butterToBandStop
![]()

test1
make a normalized butter low pass analog filter of order 4

![]()
convert to band stop

![]()
Plot the magnitude spectrums

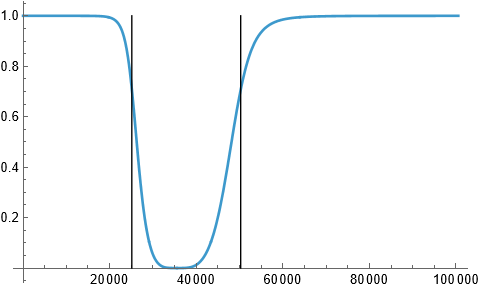
butterToHighPass
![]()

test1
make a normalized butter low pass analog filter of order 4

![]()
convert to high pass

![]()
![]()
Plot the magnitude spectrums


butterToLowPass
![]()

test1
make a normalized butter low pass analog filter of order 4

![]()
convert the cut off frequency to a new cutoff frequency

![]()
Plot the magnitude spectrums


centerImageData
![]()

![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()



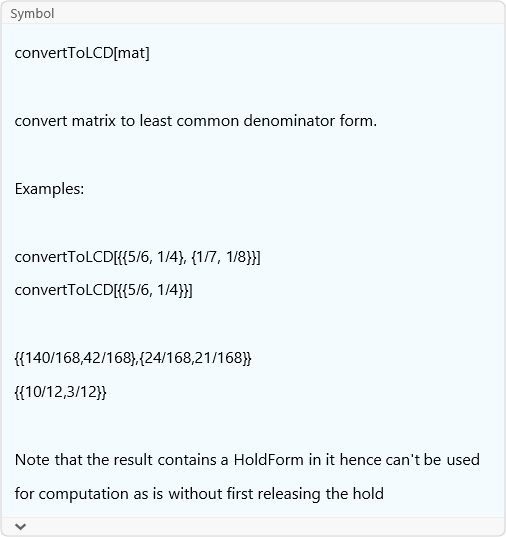
convertToLCD
![]()
![]()
![]()
![]()
![]()
diagonalBlockMatrix
![]()


![]()

diagonalDominantMatrixQ
![]()

![]()
![]()
![]()
![]()
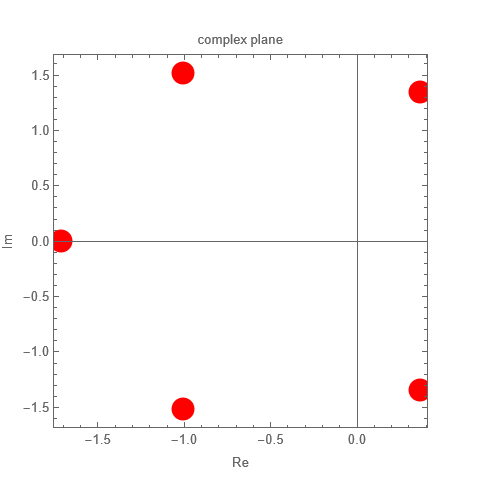
displayHurwitz
![]()

![]()
| Hurwitz Matrix | root locations | Real part of roots | ||||||||||||||||||
|
|
 |
|
fcPulseTrain
![]()

get nth fourier series complex coeff

| -4 | 0 |
| -3 | |
| -2 | 0 |
| -1 | |
| 0 | |
| 1 | |
| 2 | 0 |
| 3 | |
| 4 | 0 |
formatBinary
![]()
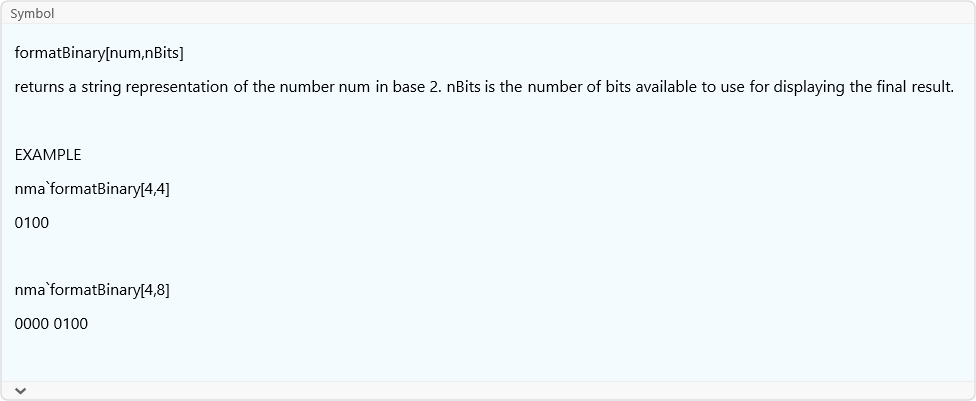
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
generateLTVControllabilityMatrix
![]()


![]()
![]()
![]()
![]()
![]()
generateLTVObservabilityMatrix
![]()



![]()
getButterworthPolynomial
![]()

Generate butterworth H(s) given order and cuttoff
test1

![]()
![]()
test2

![]()
![]()
test3

![]()
![]()
test4 find normalized Butterworth

![]()
![]()
test 5, even

![]()
![]()
getControllableForm
![]()

![]()

![]()
![]()
![]()

![]()
![]()
getMagnitudeOfPulseTrainFourierCoeff
![]()

![]()
![]()
getMaxPadding
![]()


 |
 |
getPhaseOfPulseTrainFourierCoeff
![]()

![]()
![]()
getPositiveAndNegativeTerms
![]()


![]()
![]()
getStateGainVector
![]()
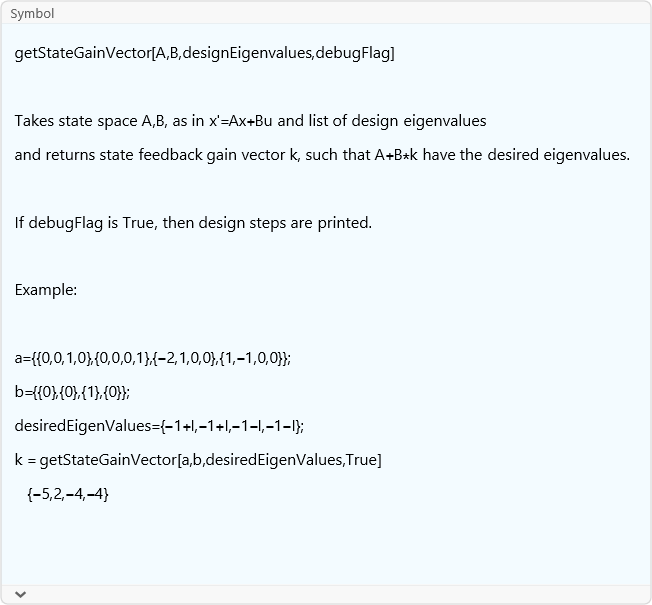

![]()
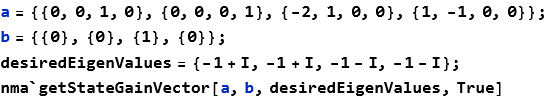

![]()






![]()
![]()
![]()
![]()
![]()
![]()
![]()
hurwitz
![]()

![]()
| 9 | 6 | 1 | 0 | 0 |
| 11 | 8 | 3 | 0 | 0 |
| 0 | 9 | 6 | 1 | 0 |
| 0 | 11 | 8 | 3 | 0 |
| 0 | 0 | 9 | 6 | 1 |
kharitonovPoly
![]()

![]()
leadingDet
![]()

![]()
![]()
![]()
linspace
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
makePulseTrain
![]()



matrix2DLexOrdering
![]()

![]()
![]()
![]()

![]()
![]()

![]()
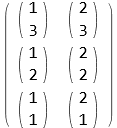
![]()
![]()

![]()

![]()
![]()
matrix2DredBlackPositions
![]()


![]()

![]()

![]()
To apply the 2D Laplacian on a matrix using red-black





numIt
![]()

![]()
![]()
![]()
numItse
![]()

![]()
![]()
![]()
![]()
![]()
![]()
plotFourierTransform
![]()




poissonMatrixOnSquareDirichlet
![]()

![]()

![]()
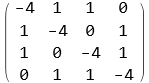
![]()

polarForm
![]()
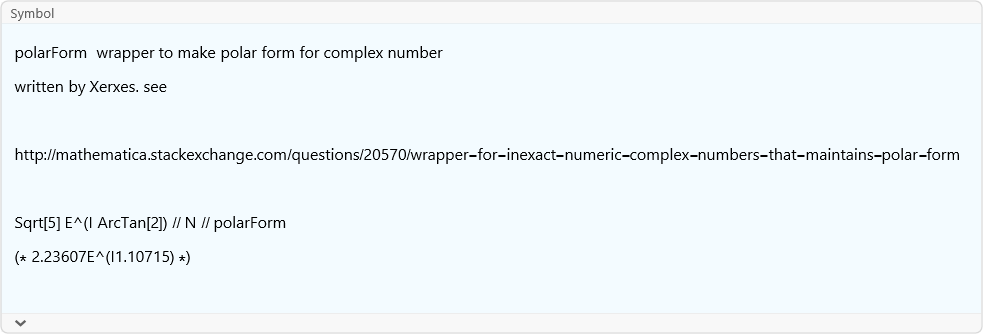
![]()
![]()
quantizationLevel
![]()
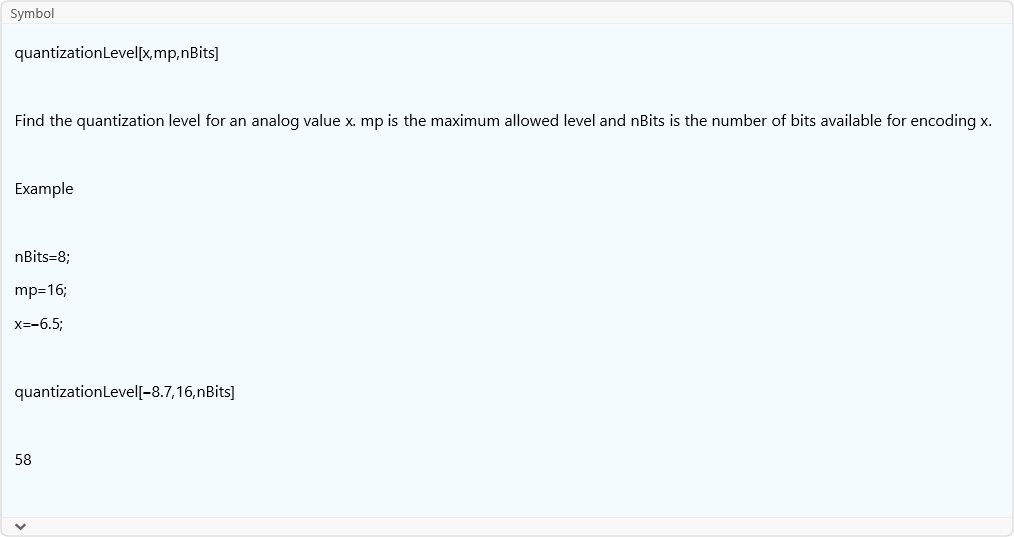

![]()
snip
![]()

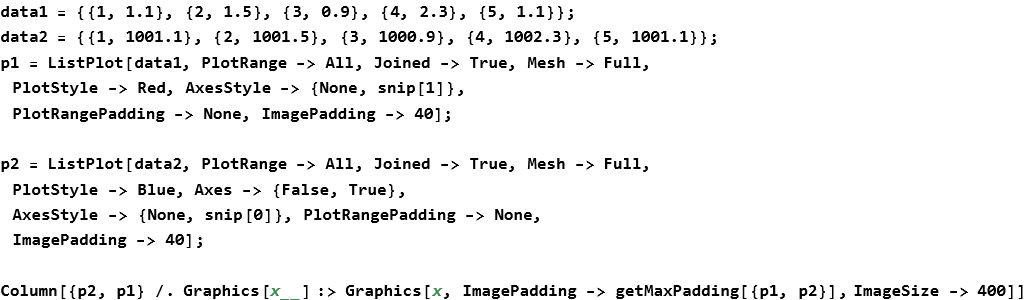
 |
 |
str
![]()

![]()
![]()
stripGraphMouseAppearance
![]()



toOffsetBinary
![]()
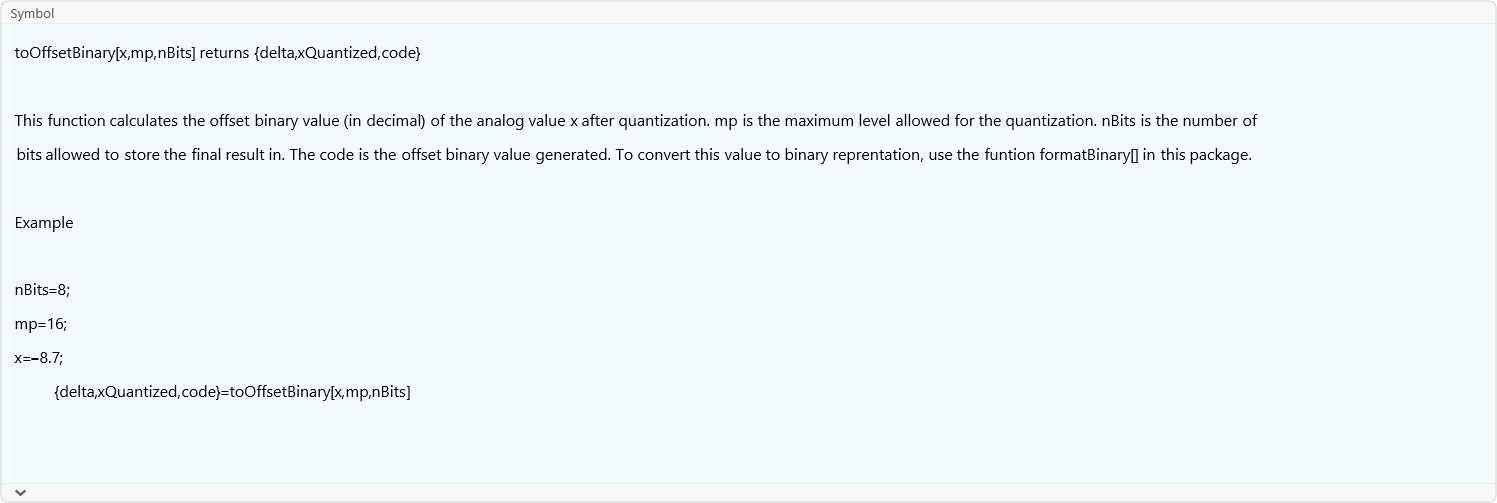

![]()
![]()
![]()

![]()
![]()
![]()

![]()
![]()
toOnesComplement
![]()


![]()
![]()
![]()

![]()
![]()
![]()
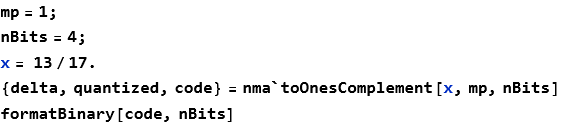
![]()
![]()
![]()

![]()
![]()

![]()
![]()

![]()
![]()
![]()
| 0.9375 | 0111 |
| 0.875 | 0111 |
| 0.8125 | 0110 |
| 0.75 | 0110 |
| 0.6875 | 0110 |
| 0.625 | 0101 |
| 0.5625 | 0100 |
| 0.5 | 0100 |
| 0.4375 | 0100 |
| 0.375 | 0011 |
| 0.3125 | 0010 |
| 0.25 | 0010 |
| 0.1875 | 0010 |
| 0.125 | 0001 |
| 0.0625 | 0000 |
| 0. | 1111 |
| -0.0625 | 1111 |
| -0.125 | 1110 |
| -0.1875 | 1101 |
| -0.25 | 1101 |
| -0.3125 | 1101 |
| -0.375 | 1100 |
| -0.4375 | 1011 |
| -0.5 | 1011 |
| -0.5625 | 1011 |
| -0.625 | 1010 |
| -0.6875 | 1001 |
| -0.75 | 1001 |
| -0.8125 | 1001 |
| -0.875 | 1000 |
| -0.9375 | 1000 |
| -1. | 1000 |
toSignMagnitude
![]()
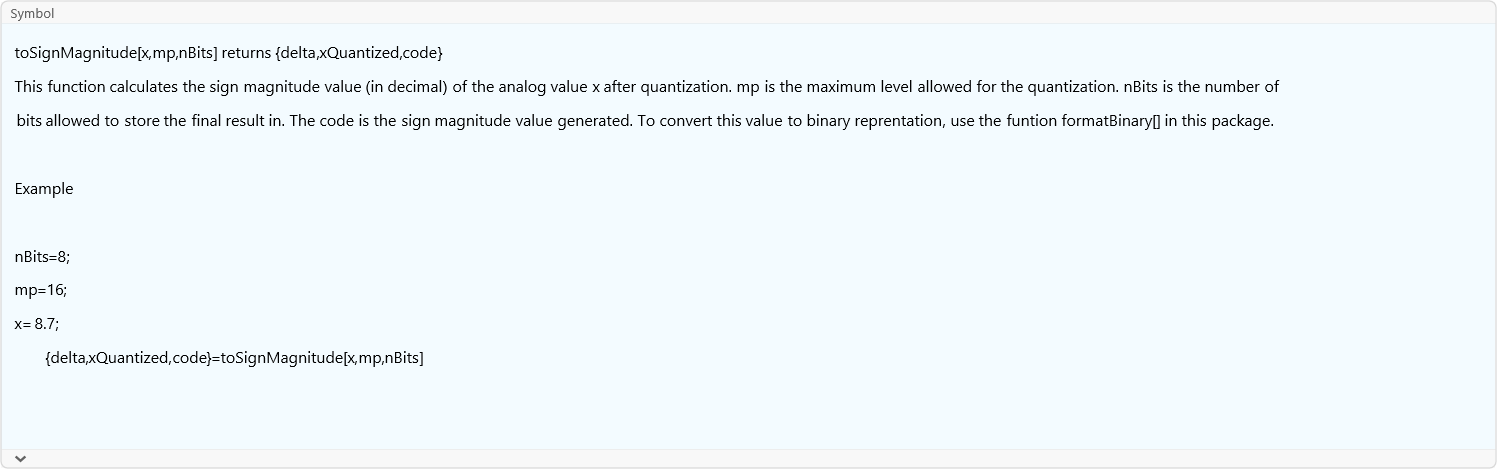

![]()
![]()
![]()

![]()
![]()

![]()
![]()

![]()
![]()

![]()
![]()

![]()
![]()

![]()
![]()
toTwoComplement
![]()


![]()
![]()
![]()

![]()
![]()
![]()
Function to obtain Fourier series approximation given fundamental period and complex fourier coefficients 0..N-1
![]()

test on a square pulse


Funtion to divide polynomial by powers of variable and keep powers in form ![]()

test

![]()
![]()
![]()
Function to convert low pass digital filter to high pass using frequency transformation
test

 |
 |
test2

 |
 |
Function to convert low pass digital filter to bandpass digital filter using frequency transformation
test

 |
 |
Function to convert low pass digital filter to bandstop digital filter by frequency transformation
test

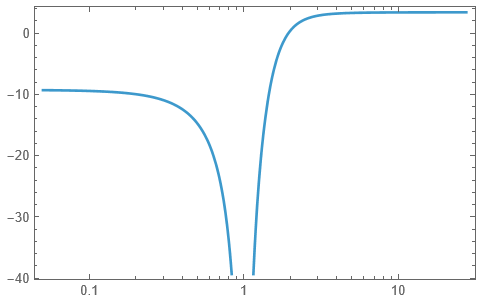 |
 |
checkForSingularity

| point | limit x p(x) | limit x^2 q(x) |
| 0 | c | 0 |
| 1 | 1+a+b-c | 0 |
| ∞ | 1-a-b | a b |

| point | limit x p(x) | limit x^2 q(x) |
| -1 | 1 | |
| 1 | 1 | |
| ∞ | 0 | ∞ |