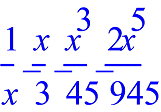4.2 HW 1

UP

PDF (letter size)

PDF (legal size)

4.2.1 Section 1.1, Problem 10

Problem: Prove or disprove this assertion: if $f$ is differentiable at $x$, then for any $\alpha \ne 1$

$$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f(x+\alpha h)}{h-\alpha h}$$

Solution:

Since $f^{\prime }(x)$ exists, then expanding $f(x+h)$ and $f(x+\alpha h)$ in Taylor series results in

$$\begin{array}{rl}f(x+h)& =f(x)+f^{\prime }(x)h+\cdots \text{(Higher Order Terms involving }{h}^m\text{ where }m\ge 2\text{)}\\ f(x+\alpha h)& =f(x)+\left(\alpha h\right)f^{\prime }(x)+\cdots \text{(Higher Order Terms involving }{\left(\alpha h\right)}^m\text{ where }m\ge 2\text{)}\end{array}$$

From first equation above we write

$$\begin{array}{}\text{(1)}& f(x)=f(x+h)-h{f}^{{}^{\prime }}(x)-(\text{Higher Order Terms involving }{h}^m\text{where }m\ge 2)\end{array}$$

And from the second equation we write

$$\begin{array}{}\text{(2)}& f(x)=f(x+\alpha h)-\left(\alpha h\right)f^{{}^{\prime }}(x)-(\text{Higher Order Terms involving }{\left(\alpha h\right)}^m\text{where }m\ge 2)\end{array}$$

equating equations (1)-(2)=0 we obtain

$$\begin{array}{rl}[f(x+h)-h{f}^{{}^{\prime }}(x)-O\left(h^m\right)]-[f(x+\alpha h)-\left(\alpha h\right)f^{{}^{\prime }}(x)-O{\left(\alpha h\right)}^m]& =0\\ f^{\prime }(x)[\alpha h-h]+f(x+h)-f(x+\alpha h)-O\left(h^m\right)+O{\left(\alpha h\right)}^m& =0\end{array}$$

Keep $f^{\prime }(x)$ on one side, and move everything to the other side results in

$$f^{\prime }(x)=\frac{f(x+\alpha h)-f(x+h)}{(\alpha h-h)}+\frac{(O\left(h^m\right)-O{\left(\alpha h\right)}^m)}{(\alpha h-h)}$$

As $h$ goes to zero the above reduces to

$$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+\alpha h)-f(x+h)}{(\alpha h-h)}$$

rearrange the sign results in

$$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f(x+\alpha h)}{(h-\alpha h)}$$

4.2.2 Section 1.1, Problem 16

Problem: If the series for $\ln x$ is truncated after the term involving ${(x-1)}^{1000}$ and is then used to compute $\ln 2$, what bound on the error can be give?

Answer:

Assume $\ln x$ has a power series expansion around $x_0$, we write, from definition of power series

$$\begin{array}{}\text{(1)}& \ln (x)=a_0+a_1(x-x_0)+a_2{(x-x_0)}^2+a_3{(x-x_0)}^3+\cdots +a_n{(x-x_0)}^n+\cdots \end{array}$$

When $x_0=1$ we get

$$\begin{array}{}\text{(2)}& \ln (x)=a_0+a_1(x-1)+a_2{(x-1)}^2+a_3{(x-1)}^3+\cdots +a_n{(x-1)}^n+\cdots \end{array}$$

At $x=1$ we obtain $a_0=0$ since $\ln (1)=0$

Differentiate (2)

$$\begin{array}{}\text{(3)}& \frac{1}{x}=a_1+2a_2(x-1)+3a_3{(x-1)}^2+\cdots +n{a}_n{(x-1)}^{n-1}+\cdots \end{array}$$

At $x=1$ we obtain $a_1=1$

Differentiate (3)

$$\begin{array}{}\text{(4)}& \frac{-1}{x^2}=2a_2+(3\times 2)a_3(x-1)+\cdots +n(n-1)a_n{(x-1)}^{n-2}+\cdots \end{array}$$

At $x=1$ we obtain $-1=2a_2\to a_2=\frac{-1}{2}$

Differentiate (4)

$$\begin{array}{}\text{(5)}& \frac{2}{x^3}=(3\times 2)a_3+\cdots +n(n-1)(n-2)a_n{(x-1)}^{n-3}+\cdots \end{array}$$

at $x=1$ we obtain $a_3=\frac{1}{3}$

continue as above, we obtain the power series for $\ln (x)$ as

$$\ln (x)=(x-1)-\frac{1}{2}{(x-1)}^2+\frac{1}{3}{(x-1)}^3-\frac{1}{4}{(x-1)}^4+\cdots +\frac{{(-1)}^{n+1}}{n}{(x-1)}^n+\cdots$$

Notice that for the above to converge, we need to have $(x-1)\le 1$, or $x\le 2$

Now if the series is truncated after ${(x-1)}^{1000}$, hence $n=1000$, and the maximum error will be the $(n+1)$ term.

Hence $$\begin{array}{rl}E& \le \left|\frac{{(-1)}^{1002}}{1001}{(x-1)}^{1001}\right|\\ & \le \frac{{(x-1)}^{1001}}{1001}\end{array}$$

which for $x=2$

$$\begin{array}{rl}E& \le \frac{{(2-1)}^{1001}}{1001}\\ & \le \frac{1}{1001}\\ & \le 9.99\times {10}^{-4}\end{array}$$

4.2.3 Section 1.1, Problem 24

Problem: For small values of $x$, how good is the approximation for $\cos x\approx 1-\frac{1}{2}{x}^2$? for what range of values will this approximation give correct results rounded to 3 decimal places?

Answer:

Expand $\cos (x)$ in power series, we write

$$\cos (x)=a_0+a_1(x-x_0)+a_2{(x-x_0)}^2+a_3{(x-x_0)}^3+\cdots +a_n{(x-x_0)}^n+\cdots$$

expand at $x_0=0$

$$\cos (x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\cdots +a_n{x}^n+\cdots$$

At $x=0\to a_0=1$, Differentiate the above

$$-\sin (x)=a_1+2a_{2}x+3a_3{x}^2+\cdots +n{a}_n{x}^{n-1}+\cdots$$

at $x=0\to a_1=0$, Differentiate the above

$$-\cos (x)=2a_2+(3\times 2)a_{3}x+\cdots +n(n-1)a_n{x}^{n-2}+\cdots$$

at $x=0\to a_2=-\frac{1}{2}$, continue as above, we obtain the series for $\cos (x)$ as

$$\cos (x)=1-\frac{1}{2}{x}^2+\frac{1}{4!}{x}^4-\cdots +\frac{{(-1)}^{n+1}}{n!}{x}^n+\cdots$$

Hence if we truncate the series at $\cos (x)\approx 1-\frac{1}{2}{x}^2$, then the maximum error will be bounded by $$E\le \frac{1}{4!}{x}^4$$

Since we want the error to be correct to 3 decimal places, then we write

$$E<0.001$$

Hence $$\begin{array}{rl}{x}^4& <4!(0.001)\\ & <0.024\end{array}$$

Hence $$x<{\left(0.024\right)}^{\frac{1}{4}}=0.39360$$

So for $x<0.39360$ radians (about $22.{552}^0$), the approximation $\cos (x)\approx 1-\frac{1}{2}{x}^2$ give correct results to 3 decimal places.

A small code to verify:

Figure 4.1:code

4.2.4 Section 1.1, Problem 32

Problem: First develop the function $\sqrt{x}$ in a series of powers of $(x-1)$ and then use it to approximate $\sqrt{0.9999999995}$ to 10 decimal places.

Solution:

$$\sqrt{x}=a_0+a_1(x-x_0)+a_2{(x-x_0)}^2+a_3{(x-x_0)}^3+\cdots +a_n{(x-x_0)}^n+\cdots$$

Expand at $x_0=1$

$$\sqrt{x}=a_0+a_1(x-1)+a_2{(x-1)}^2+a_3{(x-1)}^3+\cdots +a_n{(x-1)}^n+\cdots$$

at $x=1\to a_0=1$, differentiating the above we obtain

$$\frac{1}{2\sqrt{x}}=a_1+2a_2(x-1)+3a_3{(x-1)}^2+\cdots +n{a}_n{(x-1)}^{n-1}+\cdots$$

at $x=1\to a_1=\frac{1}{2}$, differentiate the above we obtain

$$\frac{-1}{4(x{)}^{3/2}}=2a_2+(3\times 2)a_3(x-1)+\cdots +n(n-1)a_n{(x-1)}^{n-2}+\cdots$$

at $x=1\to a_2=-\frac{1}{4\times 2}=-\frac{1}{8}$, differentiate the above we obtain

$$\frac{3}{8(x{)}^{5/2}}=(3\times 2)a_3+\cdots +n(n-1)(n-2)a_n{(x-1)}^{n-3}+\cdots$$

at $x=1\to a_3=\frac{3}{8(3\times 2)}=\frac{1}{16}$ differentiating the above gives

$$-\frac{15}{16(x{)}^{7/2}}=(4\times 3\times 2)a_4+\cdots +n(n-1)(n-2)(n-3)a_n{(x-1)}^{n-4}+\cdots$$

at $x=1\to a_4=-\frac{15}{16(4\times 3\times 2)}=-\frac{5}{128}$

Hence the series is

$$\sqrt{x}=1+\frac{1}{2}(x-1)-\frac{1}{8}{(x-1)}^2+\frac{1}{16}{(x-1)}^3-\frac{5}{128}{(x-1)}^4+\cdots$$

Note: For convergence we require $\left|x\right|\le 1$

We want accuracy to 10 decimal places. Since

$$\sqrt{0.9999999995}=0.9999999974$$

Then the series, using 2 terms gives

$$\sqrt{0.9999999995}\approx {(1+\frac{1}{2}(x-1))}_{x=0.9999999995}=1+\frac{1}{2}(0.9999999995-1)=0.9999999975$$

hence 2 terms are only needed. hence $n=1$

4.2.5 Section 1.2, problem 6(b,e)

Problem: For the pair $(x_n,{\alpha }_n)$, is it true that $x_n=O\left({\alpha }_n\right)$ as $n\to \mathrm{\infty }?$

b) $x_n=5n^2+9n^3+1,{\alpha }_n=1$

e) $x_n=\sqrt{n+3},{\alpha }_n=\frac{1}{n}$

Solution:

b) Assume that $5n^2+9n^3+1\le C\left({\alpha }_n\right)$ hence $5n^2+9n^3+1\le C$, but since $n>1$ and keeps increasing, then no matter how large a $C$ we select, $5n^2+9n^3$ will eventually become larger than any constant $C$ we choose when $n>N$ for sufficiently large $N$.

Hence there is no such $C$, hence the answer is NOT TRUE.

e) we see that $li{m}_{n\to \mathrm{\infty }}{x}_n=\mathrm{\infty }$, however $\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}=0$, hence it is not possible to find $C$ s.t. $\sqrt{n+3}\le C\frac{1}{n}$ for any $N$. Hence the answer is NOT TRUE.

4.2.6 Section 1.2, problem 7(b,c)

Problem: Choose the correct assertion (in each, $n\to \mathrm{\infty })$

b) $\frac{n+1}{\sqrt{n}}=o(1)$

c)$\frac{1}{\ln n}=O\left(\frac{1}{n}\right)$

Solution:

b) $x_n=\frac{n+1}{\sqrt{n}},{\alpha }_n=1$.

$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}\left(\frac{x_n}{{\alpha }_n}\right)& =\underset{n\to \mathrm{\infty }}{lim}\left(\frac{n+1}{\sqrt{n}}\right)\\ & =\underset{n\to \mathrm{\infty }}{lim}\left(\frac{n+1}{\sqrt{n}}\right)\\ & =\underset{n\to \mathrm{\infty }}{lim}\left(\frac{n}{\sqrt{n}}\right)+\underset{n\to \mathrm{\infty }}{lim}\left(\frac{1}{\sqrt{n}}\right)\\ & =\underset{n\to \mathrm{\infty }}{lim}\left(\sqrt{n}\right)+0\\ & \ne 0\end{array}$$

Since the limit as $n\to \mathrm{\infty }$ is not zero, hence the assertion is FALSE

c)$x_n=\frac{1}{\ln n},{\alpha }_n=\frac{1}{n}$. Since $\ln n$ grows less rapidly than $n$then $\frac{1}{\ln n}$grows more rapidly than $\frac{1}{n}$, Hence it is not possible to find some constant $C$ s.t. $\frac{1}{\ln n}\le C\frac{1}{n}$ , hence assertion is FALSE

4.2.7 Section 1.2, problem 10

Problem: Show that these assertions are not true:

a) $e^x-1=O\left(x^2\right)$ as $x\to 0$

b) $x^{-2}=O(\cot x)$ as $x\to 0$

c) $\cot x=o\left(x^{-1}\right)$ as $x\to 0$

Answer:

a) We need to $$\begin{array}{rl}{x}_n& =e^x-1\\ & =(1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots )-1\\ & =x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots \end{array}$$

and ${\alpha }_n=x^2$

As $x\to 0$the term $x$ will become larger than $x^2$, hence near $x=0$, $x_n>{\alpha }_n$ since near $x=0$ $x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots >x^2$

Therefore it is not possible to find a constant $C$ such that $x_n\le C{\alpha }_n$ near $x=0$ since for any constant $C$ we select, no matter how small, we can find $x$ closer to zero such that $x_n>C{\alpha }_n$, Hence assertion is not true.

b) The power series for $\cot (x)$ is (Using CAS:).

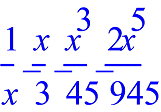Figure 4.2:code

Here we have $x_n=x^{-2}$ and ${\alpha }_n=\frac{1}{x}-\frac{x}{3}-\frac{x^3}{45}-\cdots$

As $x\to 0$, $$then ${\alpha }_n\to \frac{1}{x}$

But $\frac{1}{x}$ will grow less rapidly than $\frac{1}{x^2}$would as $x\to 0$, hence it is not possible to find a constant $C$ such that $x_n\le C{\alpha }_n$ near $x=0$ since for any constant $C$ we select, no matter how small, can find $x$ closer to zero such that $x_n>C{\alpha }_n$, Hence assertion is not true.

c) $x_n=\cot (x)=\frac{1}{x}-\frac{x}{3}-\frac{x^3}{45}-\cdots ,{\alpha }_n=\frac{1}{x}$, hence

$$\begin{array}{rl}\underset{x\to 0}{lim}\frac{x_n}{{\alpha }_n}& =\underset{x\to 0}{lim}\frac{\frac{1}{x}-\frac{x}{3}-\frac{x^3}{45}-\cdots }{\frac{1}{x}}\\ & =\underset{x\to 0}{lim}\frac{\frac{1}{x}(1-\frac{x^2}{3}-\frac{x^4}{45}-\cdots )}{\frac{1}{x}}\\ & =\underset{x\to 0}{lim}(1-\frac{x^2}{3}-\frac{x^4}{45}-\cdots )\\ & =1\end{array}$$

Since the limit does not go to zero, hence the assertion is not true.

4.2.8 Section 1.2, problem 28

Problem: Prove that $x_n=x+o(1)$ iff $\underset{n\to \mathrm{\infty }}{lim}{x}_n=x$

Solution:

Let $X_n=x_n-x,{\alpha }_n=1$

Forward direction proof:

$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}{X}_n& =\underset{n\to \mathrm{\infty }}{lim}(x_n-x)\\ & =\left(\underset{n\to \mathrm{\infty }}{lim}{x}_n\right)-\left(\underset{n\to \mathrm{\infty }}{lim}x\right)\\ & =\left(\underset{n\to \mathrm{\infty }}{lim}{x}_n\right)-x\end{array}$$

If $\underset{n\to \mathrm{\infty }}{lim}{x}_n=x$, then the above become $x-x=0$

Hence $\underset{n\to \mathrm{\infty }}{lim}\frac{X_n}{{\alpha }_n}=\frac{0}{1}=0$, hence $X_n=o(1)$ or $x_n-x=o(1)$ or $x_n=x+o(1)$

Now proof in the reverse direction. Assume that $\underset{n\to \mathrm{\infty }}{lim}{x}_n\ne x$, we need to show that this implies $x_n\ne x+o\left(1\right)$

If $\underset{n\to \mathrm{\infty }}{lim}{x}_n\ne x$, then we can say that $\underset{n\to \mathrm{\infty }}{lim}{x}_n=\beta$, where $\beta \ne x$, hence $\underset{n\to \mathrm{\infty }}{lim}{X}_n=\beta -x$

Hence $$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}\frac{X_n}{{\alpha }_n}& =\underset{n\to \mathrm{\infty }}{lim}\frac{\beta -x}{{\alpha }_n}\\ & =\frac{\beta -x}{1}\\ & =\beta -x\end{array}$$

But since $\beta \ne x$, then this limit does not go to zero. Hence $x_n\ne x+o(1)$. This complete the proof.

4.2.9 Section 1.2, problem 40

Problem: Prove: If ${\alpha }_n\to 0$, $x_n=O\left({\alpha }_n\right)$, and $y_n=O\left({\alpha }_n\right)$ then $x_n{y}_n=o\left({\alpha }_n\right)$

Answer: Since $x_n=O\left({\alpha }_n\right)$ then $x_n\le C_1\left({\alpha }_n\right)$, and since $y_n=O\left({\alpha }_n\right)$ then $y_n\le C_2\left({\alpha }_n\right),$ where $C_1,C_2$ are positive constants.

Hence $$\begin{array}{rl}{x}_n{y}_n& \le C_1{C}_2\left({\alpha }_n\right)\\ & \le C\left({\alpha }_n\right)\end{array}$$

Where $C=C_1{C}_2$

But $x_n{y}_n\le C\left({\alpha }_n\right)$ means that $x_n{y}_n$ is bounded above by ${\alpha }_n$.

But we are told next that $\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n=0$, hence this means that the sequence $x_n{y}_n$ will reach zero before the sequence ${\alpha }_n$. But this is the same as saying that $x_n{y}_n=o\left({\alpha }_n\right)$

4.2.10 Section 1.3, problem 9

Problem: Prove that if $L_1$ and $L_2$ are linear combinations of powers of $E$ and if $L_{1}x=0$, then $L_1{L}_{2}x=0$

Answer: Let $L_1=a_1{E}^{n_1}+a_2{E}^{n_2}+\cdots$ and $L_2=b_1{E}^{m_1}+b_2{E}^{m_2}+\cdots$

Then $$\begin{array}{rl}{L}_1{L}_{2}x& =(a_1{E}^{n_1}+a_2{E}^{n_2}+\cdots )(b_1{E}^{m_1}+b_2{E}^{m_2}+\cdots )x\\ & =(a_1{E}^{n_1}+a_2{E}^{n_2}+\cdots )(b_1{E}^{m_1}x+b_2{E}^{m_2}x+\cdots )\\ & \\ & =(a_1{E}^{n_1}\left(b_1{E}^{m_1}x\right)+a_2{E}^{n_2}\left(b_1{E}^{m_1}x\right)+\cdots )\\ & +(a_1{E}^{n_1}\left(b_2{E}^{m_2}x\right)+a_2{E}^{n_2}\left(b_2{E}^{m_2}x\right)+\cdots )\\ & +\cdots \\ & =(b_1{a}_1{E}^{n_1}\left(E^{m_1}x\right)+b_1{a}_2{E}^{n_2}\left(E^{m_1}x\right)+\cdots )\\ & +(b_2{a}_1{E}^{n_1}\left(E^{m_2}x\right)+b_2{a}_2{E}^{n_2}\left(E^{m_2}x\right)+\cdots )\\ & +\cdots \\ & =(b_1{a}_1{E}^{m_1}\left(E^{n_1}x\right)+b_1{a}_2{E}^{m_1}\left(E^{n_2}x\right)+\cdots )\\ & +(b_2{a}_1{E}^{m_2}\left(E^{n_1}x\right)+b_2{a}_2{E}^{m_2}\left(E^{n_2}x\right)+\cdots )\\ & +\cdots \\ & =(b_1{E}^{m_1}+b_2{E}^{m_2}+\cdots )(a_1{E}^{n_1}x+a_2{E}^{n_2}x+\cdots )\\ & =L_2{L}_{1}x\\ & =L_2(0)\\ & =0\end{array}$$

4.2.11 Section 1.3, Problem 11

Problem: Give bases consisting of real sequences for each solution space.

a) $(4E^0-3E^2+E^3)x=0$

b) $(3E^0-2E+E^2)x=0$

c) $(2E^6-9E^5+12E^4-4E^3)x=0$

d) $(\pi E^2-\sqrt{2}E+E^0\log 2)x=0$

Solution:

a) Characteristic equation is ${\lambda }^3-3{\lambda }^2+4=0$, or $(\lambda +1){(\lambda -2)}^2=0$, hence the roots are $\lambda =-1$, and $\lambda =2$ or multiplicity 2.

i.e. ${\lambda }_1=-1,{\lambda }_2=2,{\lambda }_3=2$

Hence first solution $x_1(n)$associated with ${\lambda }_1=-1$is $x_1(n)={\lambda }_1^n=-1^n$

the second solution $x_2(n)$associated with ${\lambda }_2=-2$is $x_2(n)={\lambda }_2^n=2^n$

the third solution $x_3(n)$associated with ${\lambda }_3=-2$is $x_3(n)=\frac{d{x}_2(n)}{d\lambda }=n{\lambda }_2^{n-1}=n{2}^{n-1}$

Hence now we can write some terms of the above 3 basis solutions are follows

$$\begin{array}{rl}{x}_1(n)& =[{\lambda }_1^1,{\lambda }_1^2,{\lambda }_1^3,\cdots ]\\ & =[-1,-1^2,-1^3,\cdots ]\\ & =[-1,1,-1,1,\cdots ]\\ & \\ x_2(n)& =[{\lambda }_2^1,{\lambda }_2^2,{\lambda }_2^3,\cdots ]\\ & =[2^1,2^2,2^3,\cdots ]\\ & =[2,4,8,16,32,\cdots ]\\ & \\ x_3(n)& =[{\lambda }_2^0,2{\lambda }_2^1,3{\lambda }_2^2,4{\lambda }_2^3,\cdots ]\\ & =[\left(2^0\right),2\left(2^1\right),3\left(2^2\right),4\left(2^3\right),5\left(2^4\right),\cdots ]\\ & =[1,4,12,32,80,\cdots ]\end{array}$$

Hence the basis are

$$\begin{array}{rl}& [-1,1,-1,1,\cdots ]\\ & [2,4,8,16,32,\cdots ]\\ & [1,4,12,32,80,\cdots ]\end{array}$$

b)$(3E^0-2E+E^2)x=0$

Characteristic equation is ${\lambda }^2-2\lambda +3=0$, The roots are $$\begin{array}{rl}{\lambda }_1& =1+\sqrt{2}i\\ {\lambda }_2& =1-\sqrt{2}i\end{array}$$

Hence first solution $x_1(n)$associated with ${\lambda }_1=1+\sqrt{2}i$is $x_1(n)={\lambda }_1^n={(1+\sqrt{2}i)}^n$

the second solution $x_2(n)$associated with ${\lambda }_2=1-\sqrt{2}i$is $x_2(n)={\lambda }_2^n={(1-\sqrt{2}i)}^n$

Hence $$\begin{array}{rl}{x}_1(n)& ={\lambda }_1^n\\ & =[{(1+\sqrt{2}i)}^1,{(1+\sqrt{2}i)}^2,{(1+\sqrt{2}i)}^3,\cdots ]\\ & =[(1+\sqrt{2}i),(-1+2i\sqrt{2}),(-5+i\sqrt{2}),(-7-4i\sqrt{2}),\cdots ]\\ & \\ x_2(n)& =[{(1-\sqrt{2}i)}^1,{(1-\sqrt{2}i)}^2,{(1-\sqrt{2}i)}^3,\cdots ]\\ & =[(1-\sqrt{2}i),(-1-2i\sqrt{2}),(-5-i\sqrt{2}),(-7+4i\sqrt{2})\cdots ]\end{array}$$

Notice that the 2 basis are conjugate to each others in each term in the sequence.

c)$(2E^6-9E^5+12E^4-4E^3)x=0$

Characteristic equation is $2{\lambda }^6-9{\lambda }^5+12{\lambda }^4-4{\lambda }^3=0$

Factoring we obtain $\lambda$$${}^3(2\lambda -1){(\lambda -2)}^2=0$$ hence the solutions are

$\lambda =0$ with multiplicity 3, $\lambda =\frac{1}{2},\lambda =2$ with multiplicity 2.

Hence Solutions associated with $\lambda =0$ are

$x_1(n)={\lambda }^n,x_2(n)=n{\lambda }^{n-1},x_3(n)=n(n-1){\lambda }^{n-2}$

Hence $x_1(n)=[0,0,0,\cdots ]$, and $x_2$ and $x_3$ are also the null sequence.

Solution associated with $\lambda =\frac{1}{2}$ is $x_4\left(n\right)={\lambda }^n={\left(\frac{1}{2}\right)}^n=[\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\cdots ]$

Solutions associated with $\lambda =2$ are $x_5(n)={\lambda }^n=2^n=[2,4,8,16,\cdots ]$

and $x_6(n)=\frac{d{x}_5}{d\lambda }=n{\lambda }^{n-1}=n{2}^{n-1}=[1,2(2),3\left(2^2\right),4\left(2^3\right),\cdots ]=[1,4,12,32,\cdots ]$

Hence the basis are

$$\begin{array}{rl}& [0,0,0,\cdots ]\\ & [\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\cdots ]\\ & [2,4,8,16,\cdots ]\\ & [1,4,12,32,\cdots ]\end{array}$$

d)$(\pi E^2-\sqrt{2}E+E^0\log 2)x$

Characteristic equation is $$\begin{array}{rl}\pi {\lambda }^2-\sqrt{2}\lambda +\log 2& =0\\ {\lambda }^2-\frac{\sqrt{2}}{\pi }\lambda +\frac{\log 2}{\pi }& =0\\ {\lambda }^2-0.45016\lambda +0.22064& =0\end{array}$$

$$\begin{array}{rl}\lambda & =\frac{-b\pm \sqrt{b^2-4ac}}{2a}=\frac{0.45016\pm \sqrt{0.450{16}^2-4\times 0.22064}}{2}\\ & =\frac{0.45016\pm \sqrt{-0.67992}}{2}\\ & =\frac{0.45016\pm i0.82457}{2}\end{array}$$

Hence ${\lambda }_1=0.225079+i0.41228$ and ${\lambda }_2=0.225079-i0.41228$

Hence $$\begin{array}{rl}{x}_1& ={\lambda }_1^n\\ & ={(0.225079+i0.41228)}^n\end{array}$$

and $$\begin{array}{rl}{x}_2& ={\lambda }_2^n\\ & ={(0.225079-i0.41228)}^n\end{array}$$

4.2.12 Section 1.3, Problem 12

Problem: Prove that if P is a polynomial with real coefficients and if $z\equiv [z_1,z_2,z_3,\cdots ]$ is a complex solution of $p(E)z=0,$ then the conjugate of $z$, the real part of $z$ and the imaginary part of $z$ are also solutions.

Solution:

$$P(E)z=0$$

Take conjugate of both sides

$$\begin{array}{rl}\overline{P(E)z}& =\bar{0}\\ \overline{P(E)}\bar{z}& =0\end{array}$$

But $$P(E)=a_0{E}^0+a_1{E}^1+a_2{E}^2+\cdots$$

and all the $a^{\prime }s$ are real, hence $\overline{P(E)}=P(E)$, then $$\begin{array}{}\text{(1)}& P(E)\overline{z}=0\end{array}$$

Now take the real part of $P(E)z=0$ we get

$$\begin{array}{rl}\mathrm{Re}(P(E)z)& =\mathrm{Re}(0)\\ \mathrm{Re}(P(E))\mathrm{Re}\left(z\right)& =0\end{array}$$

But $$\mathrm{Re}(P(E))=P(E)$$

Hence $$\begin{array}{}\text{(2)}& P(E)\mathrm{Re}(z)=0\end{array}$$

For the last part, let $$z=\mathrm{Re}(z)+i\mathrm{Im}(z)$$

Then $P(E)z=0$ can be written as

$$\begin{array}{rl}P(E)\{\mathrm{Re}(z)+i\mathrm{Im}(z)\}& =0\\ P(E)\mathrm{Re}(z)+iP(E)\mathrm{Im}(z)& =0\end{array}$$

But from (2) we see that $P(E)\mathrm{Re}\left(z\right)=0,$ hence the above becomes

$$iP(E)\mathrm{Im}(z)=0$$

Hence

$$P(E)\mathrm{Im}(z)=0$$

4.2.13 Section 1.3 problem 25

Problem: Determine if the difference equation $x_n=x_{n-1}+x_{n-2}$

Solution: Using the shift operator, we write $E^2{x}_{n-2}=E{x}_{n-1}+E^0{x}_{n-2}$

Hence

$$\begin{array}{rl}{E}^2{x}_{n-2}-E{x}_{n-2}-E^0{x}_{n-2}& =0\\ (E^2-E-1)x_{n-2}& =0\end{array}$$

Hence the roots of the characteristic polynomial $p(E)x=0$ are ${\lambda }^2-\lambda -1=0$ or $\lambda =\frac{-b\pm \sqrt{b^2-4ac}}{2a}$, hence $\lambda =\frac{1\pm \sqrt{1+4}}{2}=\frac{1\pm \sqrt{5}}{2}$

Hence $\left|{\lambda }_1\right|=\left|\frac{1+\sqrt{5}}{2}\right|=$ $1.618$ and $\left|{\lambda }_2\right|=\left|\frac{1-\sqrt{5}}{2}\right|$ $=0.61803$

Since ${\lambda }_1\ge 1$, then NOT STABLE difference equation.