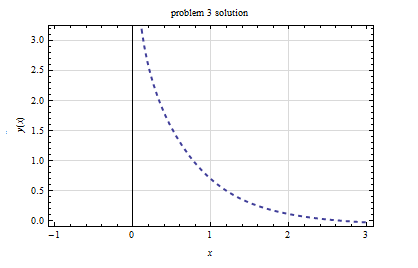
\(2yy^{\prime }=e^{x-y^{2}};y(4)=-2\)
Writing the above as \begin{align*} 2y\frac{dy}{dx} & =\frac{e^{x}}{e^{y^{2}}}\\ 2ye^{y^{2}}dy & =e^{x}dx \end{align*}
Hence the ode is separable. Integrating both sides gives\begin{equation} 2\int ye^{y^{2}}\,dy=\int e^{x}\,dx \tag{1} \end{equation} Using \(\int ye^{y^{2}}\,dy=\frac{1}{2}e^{y^{2}}\) the above reduces to \[ e^{y^{2}}=e^{x}+C \] Initial conditions are now used to find the constant of integration \(C\). Letting \(y=-2\) and \(x=4\) in the above gives\begin{align*} e^{4} & =e^{4}+C\\ C & =0 \end{align*}
Hence the solution is\begin{align*} e^{y^{2}} & =e^{x}\\ y^{2} & =x \end{align*}
Or\[ y=\pm \sqrt{x}\] To verify the solution, it is substituted back into the ode. When \(y=\sqrt{x}\) the differential equation becomes \(2\sqrt{x}\left ( \frac{1}{2\sqrt{x}}\right ) =e^{x-x}\) or \(1=1.\)
Solve \(y y^{\prime }= 2 x \sec (3 y)\) with initial conditions \(y \left ( \frac{2}{3} \right ) = \frac{\pi }{3} \)
Writing the ODE as \begin{align*} y\frac{dy}{dx} & =2x\sec \left ( 3y\right ) \\ \frac{y}{\sec \left ( 3y\right ) }dy & =2xdx \end{align*}
Hence it is separable. Integrating both side\begin{align} \int \frac{y}{\sec \left ( 3y\right ) }dy & =2\int xdx\nonumber \\ \int y\cos \left ( 3y\right ) dy & =2\int xdx \tag{1} \end{align}
Using integration by parts for \(\int y\cos \left ( 3y\right ) dy\). \(\int udv=\left [ uv\right ] -\int vdu\). Let \(u=y;dv=\cos \left ( 3y\right ) \) then \begin{align*} \int y\cos \left ( 3y\right ) dy & =\left [ y\frac{\sin \left ( 3y\right ) }{3}\right ] _{y_{0}}^{y}-\int \frac{\sin \left ( 3y\right ) }{3}dy\\ & =\left [ \frac{1}{3}y\sin \left ( 3y\right ) -y_{0}\frac{\sin \left ( 3y_{0}\right ) }{3}\right ] -\left [ \frac{1}{3}\left ( -\frac{1}{3}\cos \left ( 3y\right ) \right ) +C\right ] \\ & =\frac{1}{3}y\sin \left ( 3y\right ) +\frac{1}{9}\cos \left ( 3y\right ) +C_{1} \end{align*}
Where \(C_{1}\) is new constant that includes \(C\) and \(y_{0}\frac{\sin \left ( 3y_{0}\right ) }{3}.\) Eq. (1) becomes\[ \frac{1}{3}y\sin \left ( 3y\right ) +\frac{1}{9}\cos \left ( 3y\right ) =x^{2}+C_{2}\] Where \(C_{2}\) is new constant. Initial conditions are now used to find \(C_{2}.\) Letting \(x=\frac{2}{3}\) and \(y=\frac{\pi }{3}\) the above becomes\begin{align*} \frac{1}{3}\frac{\pi }{3}\sin \left ( 3\frac{\pi }{3}\right ) +\frac{1}{9}\cos \left ( 3\frac{\pi }{3}\right ) & =\left ( \frac{2}{3}\right ) ^{2}+C_{2}\\ C_{2} & =-\frac{1}{9}-\frac{4}{9}=\frac{-5}{9} \end{align*}
Hence solution is\[ \fbox{$3y\sin \left ( 3y\right ) +\cos \left ( 3y\right ) =9x^2-5$}\]
Solve \(\left ( 2xy+e^{y}\right ) dx+\left ( x^{2}+xe^{y}\right ) dy=0;y\left ( 1\right ) =\ln \left ( 2\right ) \)
This ODE is not separable. To check if it is exact, it is written as \[ M\left ( x,y\right ) dx+N\left ( x,y\right ) dy=0 \] Then \(\frac{\partial M}{\partial y}=2x+e^{y}\) and \(\frac{\partial N}{\partial x}=2x+e^{y}.\) Since they are the same, the differential equation is exact.
Now let \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) and \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) and the ode becomes \[ \frac{\partial \varphi \left ( x,y\right ) }{\partial x}+\frac{\partial \varphi \left ( x,y\right ) }{\partial y}\frac{dy}{dx}=0 \] or \[ \frac{d}{dx}\varphi \left ( x,y\left ( x\right ) \right ) =0 \] Which means that \(\varphi \left ( x,y\left ( x\right ) \right ) =C\). To find \(\varphi \left ( x,y\left ( x\right ) \right ) \) the equation \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) is used and integrated as follows\begin{align} \frac{\partial \varphi \left ( x,y\right ) }{\partial x} & =M\left ( x,y\right ) =2xy+e^{y}\nonumber \\ \varphi \left ( x,y\right ) & =\int \left ( 2xy+e^{y}\right ) dx\nonumber \\ & =x^{2}y+xe^{y}+g\left ( y\right ) \tag{1} \end{align}
Where \(g\left ( y\right ) \) is a function of \(y\) that needs to be found. Since \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) then\begin{equation} \frac{\partial \varphi \left ( x,y\right ) }{\partial y}=\left ( x^{2}+xe^{y}\right ) \tag{2} \end{equation} But from Eq. (1) \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=x^{2}+xe^{y}+g^{\prime }\left ( y\right ) \), hence Eq. (2) becomes\begin{align*} x^{2}+xe^{y}+g^{\prime }\left ( y\right ) & =\left ( x^{2}+xe^{y}\right ) \\ g^{\prime }\left ( y\right ) & =x^{2}+xe^{y}-x^{2}-xe^{y}\\ & =0 \end{align*}
Hence, since \(g^{\prime }\left ( y\right ) =0\) then \(g\left ( y\right ) =0\) can be chosen as solution. Therefore Eq. (1) becomes \(\varphi \left ( x,y\right ) =x^{2}y+xe^{y}\) but \(\varphi \left ( x,y\left ( x\right ) \right ) =C\) hence\[ x^{2}y+xe^{y}=C \] Initial conditions are used to find \(C\). Since \(y=\ln \left ( 2\right ) \) when \(x=1\), the above becomes \(\ln \left ( 2\right ) +e^{\ln \left ( 2\right ) }=C\) or \(C=\ln \left ( 2\right ) +2.\)Therefore, the implicit solution is \[ \fbox{$x^2y+xe^y=\ln \left ( 2\right ) +2$}\]
To verify: Taking derivative w.r.t. \(x\) gives\begin{align*} 2xy+x^{2}\frac{dy}{dx}+e^{y}+x\frac{dy}{dx}e^{y} & =0\\ \left ( 2xy+e^{y}\right ) +\frac{dy}{dx}\left ( x^{2}+xe^{y}\right ) & =0 \end{align*}
Which is the same as the original ODE.
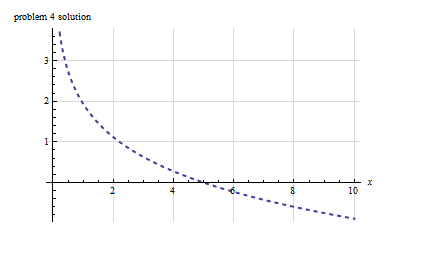
Solve \(e^{y}+\left ( xe^{y}-1\right ) y^{\prime }=0;y\left ( 5\right ) =0\)
Writing the above as \(e^{y}dx+\left ( xe^{y}-1\right ) dy=0\,.\)Letting \(M\left ( x,y\right ) =e^{y}\) and \(N\left ( x,y\right ) =\left ( xe^{y}-1\right ) \). To verify first this is exact: \(\frac{\partial M}{\partial y}=e^{y}\) and \(\frac{\partial N}{\partial x}=e^{y}\) hence they are the same and the differential equation is exact.
Letting \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) and \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) the ode becomes \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}+\frac{\partial \varphi \left ( x,y\right ) }{\partial y}\frac{dy}{dx}=0\) or \(\frac{d}{dx}\varphi \left ( x,y\left ( x\right ) \right ) =0\) hence \(\varphi \left ( x,y\left ( x\right ) \right ) =C\). To find \(\varphi \left ( x,y\left ( x\right ) \right ) \) the first equation \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) is used\begin{align} \frac{\partial \varphi \left ( x,y\right ) }{\partial x} & =M\left ( x,y\right ) =e^{y}\nonumber \\ \varphi \left ( x,y\right ) & =\int e^{y}dx\nonumber \\ & =e^{y}+g\left ( y\right ) \tag{1} \end{align}
Where \(g\left ( y\right ) \) is a function of \(y\) that needs to be found. Since \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) then\begin{equation} \frac{\partial \varphi \left ( x,y\right ) }{\partial y}=\left ( xe^{y}-1\right ) \tag{2} \end{equation} From Eq. (1) \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=e^{y}+g^{\prime }\left ( y\right ) \), hence Eq. (2) becomes\begin{align*} e^{y}+g^{\prime }\left ( y\right ) & =xe^{y}-1\\ g^{\prime }\left ( y\right ) & =e^{y}\left ( x-1\right ) -1 \end{align*}
Hence \(g\left ( y\right ) =\int \left ( e^{y}\left ( x-1\right ) -1\right ) dy=e^{y}\left ( x-1\right ) -y+C_{1}\) Therefore \begin{align*} \varphi \left ( x,y\right ) & =e^{y}+e^{y}\left ( x-1\right ) -y+C_{1}\\ & =xe^{y}-y+C_{1} \end{align*}
but \(\varphi \left ( x,y\left ( x\right ) \right ) =C\) hence\[ xe^{y}-y=C_{2}\] Initial conditions are used to find \(C_{2}\). Letting \(y=0\) when \(x=5\) the above becomes \(5\left ( 1\right ) -0=C_{2}\) hence \(C_{2}=5\). Therefore, the implicit solution is\begin{align*} xe^{y}-y & =5\\ y\left ( x\right ) & =xe^{y\left ( x\right ) }-5 \end{align*}
Solve \(\left ( 3x-y\right ) dx+\left ( 3y+x\right ) dy=0\) using general integrating factor
The ODE is Checked if it is exact: \(M\left ( x,y\right ) =3x-y\,\) hence \(\frac{\partial M}{\partial y}=-1\) and \(N\left ( x,y\right ) =3y+x\), then \(\frac{\partial N}{\partial x}=1\). Therefore it is not exact. The ODE can be made exact by using a general integration factor.
Trying \(I=\left ( x^{2}+y^{2}\right ) ^{p}\) the ODE becomes\[ \left ( x^{2}+y^{2}\right ) ^{p}\left ( 3x-y\right ) dx+\left ( x^{2}+y^{2}\right ) ^{p}\left ( 3y+x\right ) dy=0 \] Hence\begin{align*} M & =\left ( x^{2}+y^{2}\right ) ^{p}\left ( 3x-y\right ) \\ \frac{\partial M}{\partial y} & =p\left ( x^{2}+y^{2}\right ) ^{p-1}\left ( 2y\right ) \left ( 3x-y\right ) -\left ( x^{2}+y^{2}\right ) ^{p} \end{align*}
and\begin{align*} N & =\left ( x^{2}+y^{2}\right ) ^{p}\left ( 3y+x\right ) \\ \frac{\partial N}{\partial x} & =p\left ( x^{2}+y^{2}\right ) ^{p-1}\left ( 2x\right ) \left ( 3y+x\right ) +\left ( x^{2}+y^{2}\right ) ^{p} \end{align*}
For an exact ode the following is required\begin{align*} \frac{\partial M}{\partial y} & =\frac{\partial N}{\partial x}\\ 2py\left ( x^{2}+y^{2}\right ) ^{p-1}\left ( 3x-y\right ) -\left ( x^{2}+y^{2}\right ) ^{p} & =2px\left ( x^{2}+y^{2}\right ) ^{p-1}\left ( 3y+x\right ) +\left ( x^{2}+y^{2}\right ) ^{p} \end{align*}
Dividing by \(\left ( x^{2}+y^{2}\right ) ^{p-1}\)\begin{align*} p\left ( 2y\right ) \left ( 3x-y\right ) -\left ( x^{2}+y^{2}\right ) & =p\left ( 2x\right ) \left ( 3y+x\right ) +\left ( x^{2}+y^{2}\right ) \\ 2py\left ( 3x-y\right ) -\left ( x^{2}+y^{2}\right ) -2px\left ( 3y+x\right ) -\left ( x^{2}+y^{2}\right ) & =0 \end{align*}
and Letting \(p=-1\)\begin{align*} -2y\left ( 3x-y\right ) -\left ( x^{2}+y^{2}\right ) +2x\left ( 3y+x\right ) -\left ( x^{2}+y^{2}\right ) & =0\\ -6yx+2y^{2}-x^{2}-y^{2}+6xy+2x^{2}-x^{2}-y^{2} & =0\\ 0 & =0 \end{align*}
Hence the integrating factor is \[ I_{f}=\left ( x^{2}+y^{2}\right ) ^{-1}\] The ode is now multiplied by this integrating factor\begin{align*} I_{f}\left ( 3x-y\right ) dx+I_{f}\left ( 3y+x\right ) dy & =0\\ \left ( x^{2}+y^{2}\right ) ^{-1}\left ( 3x-y\right ) dx+\left ( x^{2}+y^{2}\right ) ^{-1}\left ( 3y+x\right ) dy & =0 \end{align*}
Now \(M\left ( x,y\right ) =\left ( x^{2}+y^{2}\right ) ^{-1}\left ( 3x-y\right ) \) and \(N\left ( x,y\right ) =\left ( x^{2}+y^{2}\right ) ^{-1}\left ( 3y+x\right ) .\)
Let \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) and \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) the ode becomes \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}+\frac{\partial \varphi \left ( x,y\right ) }{\partial y}\frac{dy}{dx}=0\) or \(\frac{d}{dx}\varphi \left ( x,y\left ( x\right ) \right ) =0\) hence \(\varphi \left ( x,y\left ( x\right ) \right ) =C\). To find \(\varphi \left ( x,y\left ( x\right ) \right ) ,\)the first equation \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) is used\begin{align} \frac{\partial \varphi \left ( x,y\right ) }{\partial x} & =M\left ( x,y\right ) =\left ( x^{2}+y^{2}\right ) ^{-1}\left ( 3x-y\right ) \nonumber \\ \varphi \left ( x,y\right ) & =\int \frac{\left ( 3x-y\right ) }{\left ( x^{2}+y^{2}\right ) }dx\nonumber \\ & =\frac{3}{2}\ln \left ( x^{2}+y^{2}\right ) -\arctan \left ( \frac{x}{y}\right ) +g\left ( y\right ) \tag{1} \end{align}
Where \(g\left ( y\right ) \) is a function of \(y\) that needs to be found. Since \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) then\begin{equation} \frac{\partial \varphi \left ( x,y\right ) }{\partial y}=\frac{\left ( 3y+x\right ) }{x^{2}+y^{2}} \tag{2} \end{equation} But from Eq. (1) \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=\frac{x+3y}{y^{2}+x^{2}}+g^{\prime }\left ( y\right ) \), hence Eq. (2) becomes\begin{align*} \frac{x+3y}{y^{2}+x^{2}}+g^{\prime }\left ( y\right ) & =\frac{\left ( 3y+x\right ) }{x^{2}+y^{2}}\\ g^{\prime }\left ( y\right ) & =0 \end{align*}
Since \(g^{\prime }\left ( y\right ) =0\) then \(g\left ( y\right ) =0\) is assumed. Therefore \(\varphi \left ( x,y\right ) =\frac{3}{2}\ln \left ( x^{2}+y^{2}\right ) -\arctan \left ( \frac{x}{y}\right ) \) but \(\varphi \left ( x,y\left ( x\right ) \right ) =C\) hence\[ \fbox{$\frac{3}{2}\ln \left ( x^2+y^2\right ) -\arctan \left ( \frac{x}{y}\right ) =C$}\] To find \(C\) initial conditions can be used but in this problem these are not given.
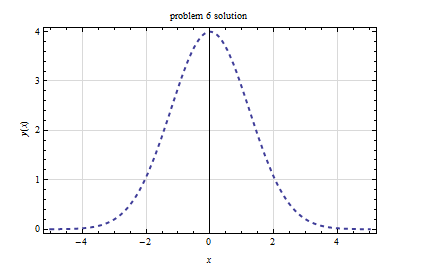
Solve \(2xy+3y^{\prime }=0;y\left ( 0\right ) =4\), using \(I_{f}=y^{a}e^{bx^{2}}\) where \(a,b\) are constants
Here \(M\left ( x,y\right ) =2xy\) and \(N\left ( x,y\right ) =3\), hence the ODE is not exact. Multiplying the ODE by \(I_{f}\) gives\[ y^{a}e^{bx^{2}}\left ( 2xy\right ) dx+y^{a}e^{bx^{2}}\left ( 3\right ) dy=0 \] Hence\begin{align*} M & =2xy^{a+1}e^{bx^{2}}\\ \frac{\partial M}{\partial y} & =2\left ( a+1\right ) xy^{a}e^{bx^{2}} \end{align*}
and\begin{align*} N & =3y^{a}e^{bx^{2}}\\ \frac{\partial N}{\partial x} & =6bxy^{a}e^{bx^{2}} \end{align*}
So for exact the following is required\begin{align*} \frac{\partial M}{\partial y} & =\frac{\partial N}{\partial x}\\ 2\left ( a+1\right ) xy^{a}e^{bx^{2}} & =6bxy^{a}e^{bx^{2}}\\ \left ( a+1\right ) & =3b \end{align*}
Hence \(b=1,a=2\). Therefore\[ I_{f}=y^{2}e^{x^{2}}\] Multiplying the ODE by the above integrating factor gives\[ \left ( y^{2}e^{x^{2}}\right ) 2xy+\left ( y^{2}e^{x^{2}}\right ) 3y^{\prime }=0=0 \] Where now \(M\left ( x,y\right ) =\left ( y^{2}e^{x^{2}}\right ) 2xy\) and \(N\left ( x,y\right ) =3\left ( y^{2}e^{x^{2}}\right ) \)
Letting \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) and \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) the ode becomes \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}+\frac{\partial \varphi \left ( x,y\right ) }{\partial y}\frac{dy}{dx}=0\) or \(\frac{d}{dx}\varphi \left ( x,y\left ( x\right ) \right ) =0\) hence \(\varphi \left ( x,y\left ( x\right ) \right ) =C\). To find \(\varphi \left ( x,y\left ( x\right ) \right ) \) the first equation \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) is used\begin{align} \frac{\partial \varphi \left ( x,y\right ) }{\partial x} & =M\left ( x,y\right ) =\left ( y^{2}e^{x^{2}}\right ) 2xy\nonumber \\ \varphi \left ( x,y\right ) & =\int 2y^{3}xe^{x^{2}}dx\nonumber \\ & =y^{3}e^{x^{2}}+g\left ( y\right ) \tag{1} \end{align}
Where \(g\left ( y\right ) \) is a function of \(y\) that needs to be found. Since \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) then\begin{equation} \frac{\partial \varphi \left ( x,y\right ) }{\partial y}=3y^{2}e^{x^{2}} \tag{2} \end{equation} From Eq. (1) \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=3y^{2}e^{x^{2}}+g^{\prime }\left ( y\right ) \), hence Eq. (2) becomes\begin{align*} 3y^{2}e^{x^{2}}+g^{\prime }\left ( y\right ) & =3y^{2}e^{x^{2}}\\ g^{\prime }\left ( y\right ) & =0 \end{align*}
Since \(g^{\prime }\left ( y\right ) =0\) then \(g\left ( y\right ) =0\) is assumed. Therefore \(\varphi \left ( x,y\right ) =y^{3}e^{x^{2}}\) but \(\varphi \left ( x,y\left ( x\right ) \right ) =C\) hence\[ y^{3}e^{x^{2}}=C \] Initial conditions are used to find \(C\) \begin{align*} \left ( 4\right ) ^{3}e^{0} & =C\\ 4^{3} & =C \end{align*}
Hence the solution is\[ y\left ( x\right ) =\left ( 4^{3}e^{-x^{2}}\right ) ^{\frac{1}{3}}\] or\[ y\left ( x\right ) =4e^{-\frac{x^{2}}{3}}\]
Why can’t one start by dividing by \(y\) in order to obtain \(2x+\frac{3}{y}y^{\prime }=0\). Hence now \(M=2x\) and \(N=\frac{3}{y}\) and so it is exact. Therefore
\(\frac{\partial \phi }{\partial x}=M=2x\), hence \(\phi =\int 2xdx=x^{2}+g\left ( y\right ) \). This means \(\frac{\partial \phi }{\partial y}=g^{\prime }\left ( y\right ) \,\) but we also know that \(\frac{\partial \phi }{\partial y}=N=\frac{3}{y}\), therefore\[ g^{\prime }\left ( y\right ) =\frac{3}{y}\] Hence \(g\left ( y\right ) =3\ln y+c_{1}\) where we can set \(c_{1}\) to any values and we choose zero. Therefore since the potential \(\phi \left ( x,y\right ) =C\) some constant, this means\begin{align*} C & =x^{2}+g\left ( y\right ) \\ C & =x^{2}+3\ln y \end{align*}
From initial conditions \(C=0+3\ln 4\), hence\begin{align*} 3\ln 4 & =x^{2}+3\ln y\\ \ln y & =\ln 4-\frac{1}{3}x^{2} \end{align*}
Or\begin{align*} y & =e^{\ln 4-\frac{1}{3}x^{2}}\\ & =4e^{\frac{x^{2}}{3}} \end{align*}
Which is the same solution found inthe key solution.
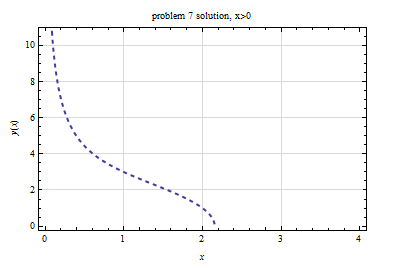
Solve \(3x^{2}y+y^{3}+2xy^{2}y^{\prime }=0;y\left ( 2\right ) =1\)
Here \(M\left ( x,y\right ) =3x^{2}y+y^{3}\) and \(N\left ( x,y\right ) =2xy^{2}\), hence \(\frac{\partial M}{\partial y}=3x^{2}+3y^{2}\) and \(\frac{\partial N}{\partial x}=2y^{2}\), therefore the ODE is not exact.
Multiplying the ODE by \(I_{f}=\frac{1}{y}\) gives\[ 3x^{2}+y^{2}+2xyy^{\prime }=0 \] To verify that the ODE is not exact\begin{align*} M & =3x^{2}+y^{2}\\ \frac{\partial M}{\partial y} & =2y \end{align*}
and\begin{align*} N & =2xy\\ \frac{\partial N}{\partial x} & =2y \end{align*}
They are the same, hence the ODE is exact. Picking the first equation \(\frac{\partial \varphi \left ( x,y\right ) }{\partial x}=M\left ( x,y\right ) \) and integrating\begin{align} \frac{\partial \varphi \left ( x,y\right ) }{\partial x} & =3x^{2}+y^{2}\nonumber \\ \varphi \left ( x,y\right ) & =\int 3x^{2}+y^{2}dx\nonumber \\ & =x^{3}+y^{2}x+g\left ( y\right ) \tag{1} \end{align}
Where \(g\left ( y\right ) \) is a function of \(y\) that needs to be found. Since \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=N\left ( x,y\right ) \) then\begin{equation} \frac{\partial \varphi \left ( x,y\right ) }{\partial y}=2xy \tag{2} \end{equation} But from Eq. (1) \(\frac{\partial \varphi \left ( x,y\right ) }{\partial y}=2yx+g^{\prime }\left ( y\right ) \), hence Eq. (2) becomes\begin{align*} 2yx+g^{\prime }\left ( y\right ) & =2xy\\ g^{\prime }\left ( y\right ) & =0 \end{align*}
Since \(g^{\prime }\left ( y\right ) =0\) then \(g\left ( y\right ) =0\) is assumed. Therefore \(\varphi \left ( x,y\right ) =x^{3}+y^{2}x\) but \(\varphi \left ( x,y\left ( x\right ) \right ) =C\) hence\[ x^{3}+y^{2}x=C \] Initial conditions are used to find the constant of integration. Using \(y\left ( 2\right ) =1\)\begin{align*} 2^{3}+1^{2}\left ( 2\right ) & =C\\ C & =10 \end{align*}
Hence the solution\begin{align*} x^{3}+y^{2}x & =10\\ y & =\pm \sqrt{\frac{10-x^{3}}{x}} \end{align*}
Find the general solution to \(x^{3}y^{\prime }=x^{2}y-y^{3}\)
The ODE is\begin{equation} \frac{dy}{dx}-\frac{1}{x}y=-\frac{1}{x^{3}}y^{3} \tag{1} \end{equation} hence it is in the form \[ y^{\prime }+p\left ( x\right ) y=f\left ( x\right ) y^{n}\] where \(p\left ( x\right ) =\frac{-1}{x}\) and \(f\left ( x\right ) =\frac{-1}{x^{3}}\) therefore a Bernoulli equation of third order since \(n=3\). To solve, it is first linearized using \(u=y^{1-n}\)\begin{align} u & =y^{-2}\tag{2}\\ \frac{du}{dy} & =-2y^{-3}\nonumber \end{align}
Hence \(\frac{dy}{du}=\frac{-1}{2}y^{3}\) \begin{align*} \frac{dy}{dx} & =\frac{dy}{du}\frac{du}{dx}\\ & =\frac{-1}{2}y^{3}\frac{du}{dx} \end{align*}
Also from Eq. (2) \[ y=u\ y^{3}\] Substituting the above 2 equations into Eq. (1) gives\[ \frac{-1}{2}y^{3}\frac{du}{dx}-\frac{1}{x}u\ y^{3}=-\frac{1}{x^{3}}y^{3}\] Dividing by \(y^{3}\) gives\begin{align*} \frac{-1}{2}\frac{du}{dx}-\frac{1}{x}u & =-\frac{1}{x^{3}}\\ \frac{du}{dx}+\frac{2}{x}u & =\frac{2}{x^{3}} \end{align*}
This is a linear ODE in \(u\left ( x\right ) \). Multiplying by integrating factor \(I\)\[ I\frac{du}{dx}+I\frac{2}{x}u=I\frac{2}{x^{3}}\] But \(\frac{d}{dx}\left ( Iu\right ) =I^{\prime }u+Iu^{\prime }\), hence comparing to the above shows that \(I^{\prime }=I\frac{2}{x}\) or \(I=e^{\int ^{x}\frac{2}{t}dt}=e^{2\ln x}=x^{2}\). The ode can now be written as\begin{align*} \frac{d}{dx}\left ( Iu\right ) & =I\frac{2}{x^{3}}\\ ux^{2} & =\int \frac{2}{x^{3}}x^{2}dx+C\\ & =2\ln x+C\\ u\left ( x\right ) & =\frac{1}{x^{2}}\left ( 2\ln x+C\right ) \end{align*}
But \(u=y^{-2}\) or \(y=\frac{1}{\sqrt{u}}\), hence \begin{align*} y\left ( x\right ) & =\pm \frac{1}{\sqrt{\frac{1}{x^{2}}\left ( 2\ln x+C\right ) }}\\ & =\pm \frac{1}{x\sqrt{2\ln x+C}} \end{align*}
Solve \(y^{\prime }=\frac{3x-y-9}{x+y+1}\)
This is of the form \(y^{\prime }=F\left ( \frac{ax+by+c}{dx+ey+r}\right ) \), since \(ae=3\) and \(bd=-1\) hence \(ae-bd=4\neq 0\), therefore this can be transformed to nearly homogeneous using \(X=x+h\) and \(Y=y+k\) as follows.
\(x=X-h\), hence \(dx=dX\) and \(y=Y-k\), hence \(dy=dY\). The ODE becomes\begin{align*} \frac{dY}{dX} & =\frac{3\left ( X-h\right ) -\left ( Y-k\right ) -9}{\left ( X-h\right ) +\left ( Y-k\right ) +1}\\ & =\frac{3X-3h-Y+k-9}{X-h+Y-k+1}\\ & =\frac{3X-Y+\left ( -3h+k-9\right ) }{X+Y+\left ( -h-k+1\right ) } \end{align*}
Now \(h,k\) are found to make \(\left ( -3h+k-9\right ) =0\) and \(\left ( -h-k+1\right ) =0\). Solving for these gives \(h=-2,k=3\), hence\begin{align*} x & =X+2\\ y & =Y-3 \end{align*}
And the ODE becomes\begin{align} \frac{dY}{dX} & =\frac{3X-Y}{X+Y}\nonumber \\ & =\frac{3-Y/X}{1+Y/X} \tag{1} \end{align}
For \(X\neq 0\) or \(x\neq 2\). Letting \(Y=UX\), then \(\frac{dY}{dX}=\frac{dU}{dX}X+U\) and Eq. (1) becomes\begin{align*} \frac{dU}{dX}X+U & =\frac{3-U}{1+U}\\ \frac{dU}{dX}X & =\frac{3-U}{1+U}-U\\ & =\frac{3-U-U\left ( 1+U\right ) }{1+U}\\ & =\frac{3-2U-U^{2}}{1+U} \end{align*}
Hence it is now separable\begin{align*} \frac{1+U}{3-2U-U^{2}}dU & =\frac{1}{X}dX\\ \int \frac{1+U}{3-2U-U^{2}}dU & =\ln \left ( X\right ) +C\\ -\frac{1}{2}\ln \left ( 3-2U-U^{2}\right ) & =\ln \left ( X\right ) +C\\ 3-2U-U^{2} & =e^{-2\ln \left ( X\right ) +C}\\ 3-2U-U^{2} & =CX^{-2} \end{align*}
Since \(Y=UX\) then\begin{align*} 3-2\left ( \frac{Y}{X}\right ) -\left ( \frac{Y}{X}\right ) ^{2} & =CX^{-2}\\ 3X^{2}-2XY-Y^{2} & =C \end{align*}
Transforming back to \(x,y\). From \(X=x-2\) and \(Y=y+3\), the above becomes\[ 3\left ( x-2\right ) ^{2}-2\left ( x-2\right ) \left ( y+3\right ) -\left ( y+3\right ) ^{2}=C \] The above is the general solution.
Find general solution to \(\left ( 2x^{2}-y^{2}\right ) dx+3xydy=0\)
This is of the form \begin{align} \frac{dy}{dx} & =\frac{y^{2}-2x^{2}}{3xy}\nonumber \\ \frac{dy}{dx} & =\frac{y^{2}}{3xy}-\frac{2x^{2}}{3xy}\nonumber \\ \frac{dy}{dx}-\frac{1}{3x}y & =-\frac{2x}{3}y^{-1}\tag{1}\\ y^{\prime }+p\left ( x\right ) y & =f\left ( x\right ) y^{n}\nonumber \end{align}
Where \(p\left ( x\right ) =\frac{-1}{3x}\) and \(f\left ( x\right ) =-\frac{2x}{3}\) and \(n=-1\), hence it is a Bernoulli equation of order \(-1.\) Using the substitution \(u=y^{1-n}\)\begin{align} u & =y^{2}\tag{2}\\ \frac{du}{dy} & =2y\nonumber \end{align}
Hence \(\frac{dy}{du}=\frac{1}{2y}\) \begin{align*} \frac{dy}{dx} & =\frac{dy}{du}\frac{du}{dx}\\ & =\frac{1}{2y}\frac{du}{dx} \end{align*}
And from Eq. (2) \[ y=\frac{u}{y}\] Substituting the above 2 equations into Eq (1) gives\[ \frac{1}{2y}\frac{du}{dx}-\frac{1}{3x}\frac{u}{y}=-\frac{2x}{3y}\] The term \(\frac{1}{y}\) cancels resulting in\begin{align*} \frac{1}{2}\frac{du}{dx}-\frac{1}{3x}u & =-\frac{2x}{3}\\ \frac{du}{dx}-\frac{2}{3x}u & =-\frac{4x}{3} \end{align*}
This is a linear ODE in \(u\left ( x\right ) \). Multiplying by an integrating factor \(I\)\[ I\frac{du}{dx}-I\frac{2}{3x}u=I\left ( \frac{-4x}{3}\right ) \] But \(\frac{d}{dx}\left ( Iu\right ) =I^{\prime }u+Iu^{\prime }\), hence \(I^{\prime }=-I\frac{2}{3x}\) or \(I=e^{\int ^{x}\frac{-2}{3t}dt}=e^{-\frac{2}{3}\ln x}=x^{-\frac{2}{3}}\), and the above ode becomes\begin{align*} \frac{d}{dx}\left ( Iu\right ) & =I\left ( \frac{-4x}{3}\right ) \\ Iu & =\int \left ( \frac{-4x}{3}\right ) Idx+C\\ u & =\frac{1}{I}\int \left ( \frac{-4x}{3}\right ) Idx+\frac{C}{I} \end{align*}
But \(I=x^{-\frac{2}{3}}\), therefore\begin{align*} u & =\frac{1}{x^{-\frac{2}{3}}}\int \left ( \frac{-4x}{3}\right ) x^{-\frac{2}{3}}dx+\frac{C}{x^{-\frac{2}{3}}}\\ & =-\frac{4}{3}x^{\frac{2}{3}}\int x^{\frac{1}{3}}dx+Cx^{\frac{2}{3}}\\ & =-\frac{4}{3}x^{\frac{2}{3}}\frac{3}{4}x^{\frac{4}{3}}+Cx^{\frac{2}{3}}\\ & =-x^{2}+Cx^{\frac{2}{3}} \end{align*}
Since \(u=y^{2}\), then \(y=\pm \sqrt{u}\), and the solution becomes\[ y\left ( x\right ) =\pm \sqrt{-x^{2}+Cx^{\frac{2}{3}}}\]
Problem: Show that if one solution, say \(y=u(x)\), of the Riccati equation \(y^{\prime }=P(x)y^{2}+Q(x)y+R(x)\) is known, then the substitution \(y=u+\frac{1}{z}\) will transform this equation into a linear first-order equation in the new dependent variable \(z\).
Using \(y=u+\frac{1}{z}\) then \(y^{\prime }=u^{\prime }-\frac{1}{z^{2}}z^{\prime }\). Substituting this into the original ODE\begin{align} u^{\prime }-\frac{1}{z^{2}}z^{\prime } & =P\left ( u+\frac{1}{z}\right ) ^{2}+Q\left ( u+\frac{1}{z}\right ) +R\nonumber \\ z^{2}u^{\prime }-z^{\prime } & =z^{2}P\left ( u^{2}+\frac{1}{z^{2}}+2\frac{u}{z}\right ) +z^{2}Qu+z^{2}\frac{Q}{z}+z^{2}R\nonumber \\ z^{2}u^{\prime }-z^{\prime } & =P\left ( z^{2}u^{2}+1+2zu\right ) +z^{2}Qu+zQ+z^{2}R\nonumber \\ z^{\prime } & =z^{2}u^{\prime }-Pz^{2}u^{2}-P-2Pzu-z^{2}Qu-zQ-z^{2}R\nonumber \\ & =z^{2}\left ( u^{\prime }-Pu^{2}-Qu-R\right ) +z\left ( -2Pu-Q\right ) -P \tag{1} \end{align}
For this to be linear, the term multiplying \(z^{2}\) must vanish. Hence\[ \Delta =u^{\prime }-Pu^{2}-Qu-R \] must be shown to be zero. Now, since \(u^{\prime }=y^{\prime }\,\ \) and \(u=y\) and \(u^{2}=y^{2}\) this term can be written as\[ \Delta =y^{\prime }-\left ( Py^{2}+Qy+R\right ) \] But from the original ODE itself, it is seen that \(y^{\prime }=Py^{2}+Qy+R\), therefore \[ \Delta =0 \] And Eq(1) becomes\[ z^{\prime }=z\left ( -2Pu-Q\right ) -P \] Or\[ z^{\prime }\left ( x\right ) +z\left ( x\right ) \left ( 2P\left ( x\right ) u\left ( x\right ) +Q\left ( x\right ) \right ) =-P\left ( x\right ) \] This is now in the form\[ z^{\prime }\left ( x\right ) +A\left ( x\right ) z\left ( x\right ) =B\left ( x\right ) \] Where \(A\left ( x\right ) =2P\left ( x\right ) u\left ( x\right ) +Q\left ( x\right ) \) and \(B\left ( x\right ) =-P\left ( x\right ) \). Since this derivation was carried out using general expressions, then it is valid for any solution \(u\left ( x\right ) \). Hence if one solution is known, the ODE can be transformed to linear first order in the new variable.