Find the inverse Laplace transform of
G\left ( s\right ) =\ln \left ( \frac{s^{2}+1}{s\left ( s+1\right ) }\right )
Answer:
Using the property \mathcal{L}\left ( tg\left ( t\right ) \right ) =-\frac{d}{ds}G\left ( s\right ) , then tg\left ( t\right ) =-\mathcal{L}^{-1}\left ( \frac{d}{ds}G\left ( s\right ) \right ) . Let f\left ( s\right ) =\frac{s^{2}+1}{s\left ( s+1\right ) } then\begin{align*} \frac{d}{ds}G\left ( s\right ) & =\frac{d}{ds}\ln \left ( f\left ( s\right ) \right ) \\ & =\frac{f^{\prime }\left ( s\right ) }{f\left ( s\right ) }\\ & =\frac{s\left ( s+1\right ) }{s^{2}+1}\frac{d}{ds}\left ( \frac{s^{2}+1}{s\left ( s+1\right ) }\right ) \\ & =\frac{s\left ( s+1\right ) }{s^{2}+1}\frac{d}{ds}\left ( \frac{s^{2}}{s\left ( s+1\right ) }+\frac{1}{s\left ( s+1\right ) }\right ) \\ & =\frac{s\left ( s+1\right ) }{s^{2}+1}\left [ \frac{d}{ds}\left ( \frac{s}{\left ( s+1\right ) }\right ) +\frac{d}{ds}\left ( \frac{1}{s\left ( s+1\right ) }\right ) \right ] \\ & =\frac{s\left ( s+1\right ) }{s^{2}+1}\left [ \frac{1}{\left ( s+1\right ) ^{2}}-\frac{1}{s^{2}}\frac{2s+1}{\left ( s+1\right ) ^{2}}\right ] \\ & =\frac{s}{s^{2}+1}\left [ \frac{1}{s+1}-\frac{1}{s^{2}}\frac{2s+1}{\left ( s+1\right ) }\right ] \\ & =\frac{s}{\left ( s^{2}+1\right ) \left ( s+1\right ) }-\frac{1}{s}\frac{2s+1}{\left ( s^{2}+1\right ) \left ( s+1\right ) }\\ & =\frac{s^{2}-2s-1}{s\left ( s^{2}+1\right ) \left ( s+1\right ) } \end{align*}
Using partial fractions \frac{s^{2}-2s-1}{s\left ( s^{2}+1\right ) \left ( s+1\right ) }=\frac{A}{s}+\frac{Bs+C}{s^{2}+1}+\frac{D}{s+1}\,, hence \begin{align*} s^{2}-2s-1 & =A\left ( s^{2}+1\right ) \left ( s+1\right ) +\left ( Bs+C\right ) s\left ( s+1\right ) +Ds\left ( s^{2}+1\right ) \\ & =A\left ( s^{3}+s^{2}+s+1\right ) +\left ( Bs^{3}+Bs^{2}+Cs^{2}+Cs\right ) +Ds^{3}+Ds\\ & =s^{3}\left ( A+B+D\right ) +s^{2}\left ( A+B+C\right ) +s\left ( A+C+D\right ) +A \end{align*}
Comparing coefficients gives, A=-1 And \begin{align*} B+D & =1\\ B+C & =2\\ C+D & =0 \end{align*}
Hence B=1-D, and from second equation 1-D+C=2 or C=D+1, hence from third equation D+1+D=-1 or D=-1 hence C=0 and B=2, therefore \frac{s^{2}-2s-1}{s\left ( s^{2}+1\right ) \left ( s+1\right ) }=-\frac{1}{s}+\frac{2s}{s^{2}+1}-\frac{1}{s+1} Now the inverse Laplace transform can be found. Using \mathcal{L}^{-1}\left ( \frac{s}{s^{2}+a}\right ) =\cos \left ( at\right ) then \mathcal{L}^{-1}\left ( \frac{s}{s^{2}+1}\right ) =\cos t and\begin{align*} tg\left ( t\right ) & =-\mathcal{L}^{-1}\left ( -\frac{1}{s}+\frac{2s}{s^{2}+1}-\frac{1}{s+1}\right ) \\ & =-\left ( -1+2\cos t-e^{-t}\right ) \end{align*}
Therefore g\left ( t\right ) =\frac{1}{t}\left ( 1-2\cos t+e^{-t}\right )
Use Laplace transform to solve \left ( 1-t\right ) y^{\prime \prime }+ty^{\prime }-y=0 with IC y\left ( 0\right ) =3 and y^{\prime }\left ( 0\right ) =-1
Answer:\begin{align*} \mathcal{L}\left ( \left ( 1-t\right ) y^{\prime \prime }+ty^{\prime }-y\right ) & =\mathcal{L}\left ( y^{\prime \prime }-ty^{\prime \prime }+ty^{\prime }-y\right ) \\ & =\left ( s^{2}Y-sy\left ( 0\right ) -y^{\prime }\left ( 0\right ) \right ) +\frac{d}{ds}\left ( s^{2}Y-sy\left ( 0\right ) -y^{\prime }\left ( 0\right ) \right ) -\frac{d}{ds}\left ( sY-y\left ( 0\right ) \right ) -Y \end{align*}
Substituting IC gives\begin{align*} \mathcal{L}\left ( \left ( 1-t\right ) y^{\prime \prime }+ty^{\prime }-y\right ) & =\left ( s^{2}Y-3s+1\right ) +\frac{d}{ds}\left ( s^{2}Y-3s+1\right ) -\frac{d}{ds}\left ( sY-3\right ) -Y\\ & =s^{2}Y-3s+1+2sY+s^{2}Y^{\prime }-3-Y-sY^{\prime }-Y\\ & =Y^{\prime }\left ( s^{2}-s\right ) +Y\left ( s^{2}+2s-2\right ) -3s-2 \end{align*}
Therefore\begin{align*} Y^{\prime }\left ( s^{2}-s\right ) +Y\left ( s^{2}+2s-2\right ) & =3s+2\\ Y^{\prime }+Y\frac{\left ( s^{2}+2s-2\right ) }{\left ( s^{2}-s\right ) } & =\frac{3s+2}{\left ( s^{2}-s\right ) } \end{align*}
Integrating factor is I_{f}=e^{\int \frac{\left ( s^{2}+2s-2\right ) }{\left ( s^{2}-s\right ) }ds} where \begin{align*} \int \frac{\left ( s^{2}+2s-2\right ) }{\left ( s^{2}-s\right ) }ds & =\int 1+\frac{1}{s-1}+\frac{2}{s}ds\\ & =s+\ln \left ( s-1\right ) +2\ln s \end{align*}
Hence \begin{align*} I_{f} & =e^{\left ( s+2\ln s+\ln \left ( s-1\right ) \right ) }\\ & =e^{s}s^{2}\left ( s-1\right ) \end{align*}
Hence\begin{align*} d\left ( I_{f}Y\right ) & =I_{f}\frac{3s+2}{\left ( s^{2}-s\right ) }\\ I_{f}Y & =\int I_{f}\frac{3s+2}{\left ( s^{2}-s\right ) }ds+c\\ & =\int e^{s}s^{2}\left ( s-1\right ) \frac{3s+2}{\left ( s^{2}-s\right ) }ds+c\\ & =\int e^{s}s\left ( 3s+2\right ) ds+c\\ & =\int 3s^{2}e^{s}ds+\int 2se^{s}ds+c\\ & =3e^{s}\left ( s^{2}-2s+2\right ) +2e^{s}\left ( s-1\right ) +c \end{align*}
Hence\begin{align*} Y & =\frac{3e^{s}\left ( s^{2}-2s+2\right ) +2e^{s}\left ( s-1\right ) }{e^{s}s^{2}\left ( s-1\right ) }+\frac{c}{e^{s}s^{2}\left ( s-1\right ) }\\ & =3\frac{\left ( s^{2}-2s+2\right ) }{s^{2}\left ( s-1\right ) }+2\frac{1}{s^{2}}+c\frac{e^{-s}}{s^{2}\left ( s-1\right ) }\\ & =\left ( 3\frac{1}{s-1}-6\frac{1}{s^{2}}\right ) +2\frac{1}{s^{2}}+c\frac{e^{-s}}{s^{2}\left ( s-1\right ) }\\ & =\frac{3}{s-1}-4\frac{1}{s^{2}}+ce^{-s}\left ( \frac{1}{s-1}-\frac{1}{s}-\frac{1}{s^{2}}\right ) \end{align*}
Therefore, inverse Laplace transform is\begin{align*} y\left ( t\right ) & =3e^{t}-4t+cH\left ( t-1\right ) \left ( e^{\left ( t-1\right ) }-1-\left ( t-1\right ) \right ) \\ & =3e^{t}-4t+cH\left ( t-1\right ) \left ( e^{\left ( t-1\right ) }-t\right ) \end{align*}
And the solution is y\left ( t\right ) =\left \{ \begin{array} [c]{ccc}3e^{t}-4t & & 0\leq t<1\\ 3e^{t}-4t+c\left ( e^{\left ( t-1\right ) }-t\right ) & & 1\leq t \end{array} \right . Notice that there is not enough information given in the problem to find the constant c for the solution 1\leq t.
Solve the initial value problem where f\left ( t\right ) is periodic y^{\prime }+4y+3\int _{0}^{t}y\left ( \tau \right ) d\tau =f\left ( t\right ) And f\left ( t\right ) =\left \{ \begin{array} [c]{ccc}1 & & 0<t<2\\ -1 & & 2<t<4 \end{array} \right . And y\left ( 0\right ) =1.
Solution:
The Laplace transform of periodic function f\left ( t\right ) with period k is F\left ( s\right ) =\frac{1}{1-e^{-ks}}\int _{0}^{k}f\left ( t\right ) e^{-st}dt For the above function k=4 and\begin{align*} \int _{0}^{4}f\left ( t\right ) e^{-st}dt & =\int _{0}^{2}e^{-st}dt-\int _{2}^{4}e^{-st}dt\\ & =\left . \frac{e^{-st}}{-s}\right \vert _{0}^{2}-\left . \frac{e^{-st}}{-s}\right \vert _{2}^{4}\\ & =\frac{-1}{s}\left ( e^{-2s}-1\right ) +\frac{1}{s}\left ( e^{-4s}-e^{-2s}\right ) \\ & =\frac{-e^{-2s}}{s}+\frac{1}{s}+\frac{e^{-4s}}{s}-\frac{e^{-2s}}{s}\\ & =\frac{1}{s}\left ( 1-2e^{-2s}+e^{-4s}\right ) \end{align*}
Hence \begin{align*} F\left ( s\right ) & =\left ( \frac{1}{1-e^{-4s}}\right ) \frac{1-2e^{-2s}+e^{-4s}}{s}\\ & =\frac{1}{s}\left ( \frac{1}{1-e^{-4s}}\right ) \left ( 1-e^{-2s}\right ) ^{2}\\ & =\frac{1}{s}\left ( \frac{1}{\left ( 1-e^{-2s}\right ) \left ( 1+e^{-2s}\right ) }\right ) \left ( 1-e^{-2s}\right ) ^{2}\\ & =\frac{1}{s}\frac{\left ( 1-e^{-2s}\right ) }{\left ( 1+e^{-2s}\right ) } \end{align*}
Using \frac{1}{1+x}=1-x+x^{2}-x^{3}+ \cdots the above can be written as (using e^{-2s} as x)\begin{align*} F\left ( s\right ) & =\frac{1}{s}\left ( 1-e^{-2s}\right ) \left ( 1-e^{-2s}+e^{-4s}-e^{-6s}+e^{-8s}-e^{-10s}\cdots \right ) \\ & =\frac{1}{s}\left [ \left ( 1-e^{-2s}+e^{-4s}-e^{-6s}+e^{-8s}-e^{-10s}+\cdots \right ) +\left ( -e^{-2s}+e^{-4s}-e^{-6s}+e^{-8s}-e^{-10s}\cdots \right ) \right ] \\ & =\frac{1}{s}\left ( 1-2e^{-2s}+2e^{-4s}-2e^{-6s}+2e^{-8s}+\cdots \right ) \end{align*}
Now taking the Laplace transform of the ODE gives \left ( sY-y\left ( 0\right ) \right ) +4Y+3\mathcal{L}\left ( \int _{0}^{t}y\left ( \tau \right ) d\tau \right ) =\frac{1}{s}\left ( 1-2e^{-2s}+2e^{-4s}-2e^{-6s}+2e^{-8s}+\cdots \right ) Using the property that \mathcal{L}^{-1}\left ( \frac{1}{s}Y\left ( s\right ) \right ) =\int _{0}^{t}y\left ( \tau \right ) d\tau , therefore \frac{1}{s}Y\left ( s\right ) =\mathcal{L}\left ( \int _{0}^{t}y\left ( \tau \right ) d\tau \right ) where Y\left ( s\right ) =\mathcal{L}\left ( y\left ( t\right ) \right ) , hence the above becomes\begin{align*} \left ( sY-1\right ) +4Y+3\frac{Y}{s} & =\frac{1}{s}\left ( 1-2e^{-2s}+2e^{-4s}-2e^{-6s}+2e^{-8s}+\cdots \right ) \\ Y\left ( s+4+\frac{3}{s}\right ) & =1+\frac{1}{s}\left ( 1-2e^{-2s}+2e^{-4s}-2e^{-6s}+2e^{-8s}+\cdots \right ) \\ Y & =\frac{s}{s^{2}+4s+3}+\frac{1}{s\left ( s+4+\frac{3}{s}\right ) }\left ( 1-2e^{-2s}+2e^{-4s}-2e^{-6s}+2e^{-8s}+\cdots \right ) \\ & =\frac{s}{s^{2}+4s+3}+\frac{1}{s^{2}+4s+3}\left ( 1-2e^{-2s}+2e^{-4s}-2e^{-6s}+2e^{-8s}+\cdots \right ) \\ & =\frac{s}{\left ( s+3\right ) \left ( s+1\right ) }+\frac{1}{\left ( s+3\right ) \left ( s+1\right ) }\left ( 1-2e^{-2s}+2e^{-4s}-2e^{-6s}+2e^{-8s}+\cdots \right ) \\ & =\frac{s}{\left ( s+3\right ) \left ( s+1\right ) }+\frac{1}{\left ( s+3\right ) \left ( s+1\right ) }-\frac{2e^{-2s}}{\left ( s+3\right ) \left ( s+1\right ) }\\ & +\frac{2e^{-4s}}{\left ( s+3\right ) \left ( s+1\right ) }-\frac{2e^{-6s}}{\left ( s+3\right ) \left ( s+1\right ) }+\frac{2e^{-8s}}{\left ( s+3\right ) \left ( s+1\right ) }-\cdots \end{align*}
Partial fractions of \frac{2}{\left ( s+3\right ) \left ( s+1\right ) }=\frac{1}{s+1}-\frac{1}{s+3} and Partial fractions of \frac{1}{\left ( s+3\right ) \left ( s+1\right ) }=\frac{1}{2\left ( s+1\right ) }-\frac{1}{2\left ( s+3\right ) } and partial fractions of \frac{s}{\left ( s+3\right ) \left ( s+1\right ) }=\frac{3}{2\left ( s+3\right ) }-\frac{1}{2\left ( s+1\right ) } and using the property \mathcal{L}^{-1}\left ( e^{-as}f\left ( s\right ) \right ) =H\left ( t-a\right ) f\left ( t-a\right ) and since \mathcal{L}^{-1}\frac{1}{s+1}=e^{-t} and \mathcal{L}^{-1}\frac{1}{s+3}=e^{-3t}, hence the inverse Transform of the above can be written as\begin{align*} y\left ( t\right ) & =\mathcal{L}^{-1}\left ( \frac{3}{2\left ( s+3\right ) }-\frac{1}{2\left ( s+1\right ) }\right ) \\ & +\mathcal{L}^{-1}\left ( \frac{1}{2\left ( s+1\right ) }-\frac{1}{2\left ( s+3\right ) }\right ) \\ & -\mathcal{L}^{-1}\left ( \frac{e^{-2s}}{s+1}-\frac{e^{-2s}}{s+3}\right ) \\ & +\mathcal{L}^{-1}\left ( \frac{e^{-4s}}{s+1}-\frac{e^{-4s}}{s+3}\right ) \\ & -\mathcal{L}^{-1}\left ( \frac{e^{-6s}}{s+1}-\frac{e^{-6s}}{s+3}\right ) +\cdots \end{align*}
Hence\begin{align*} y\left ( t\right ) & =\frac{3}{2}e^{-3t}-\frac{1}{2}e^{-t}\\ & +\frac{1}{2}e^{-t}-\frac{1}{2}e^{-3t}\\ & -H\left ( t-2\right ) \left ( e^{-\left ( t-2\right ) }-e^{-3\left ( t-2\right ) }\right ) \\ & +H\left ( t-4\right ) \left ( e^{-\left ( t-4\right ) }-e^{-3\left ( t-4\right ) }\right ) \\ & -H\left ( t-6\right ) \left ( e^{-\left ( t-6\right ) }-e^{-3\left ( t-6\right ) }\right ) +\cdots \end{align*}
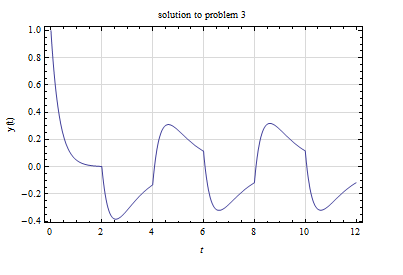
Or y\left ( t\right ) =e^{-3t}-H\left ( t-2\right ) \left ( e^{-\left ( t-2\right ) }-e^{-3\left ( t-2\right ) }\right ) +H\left ( t-4\right ) \left ( e^{-\left ( t-4\right ) }-e^{-3\left ( t-4\right ) }\right ) -H\left ( t-6\right ) \left ( e^{-\left ( t-6\right ) }-e^{-3\left ( t-6\right ) }\right ) +\cdots Here is a plot of the solution. It shows the response to be periodic, of same period as the forcing function.
Solution:
The problem as stated had a typo in it. It was updated to read x^{\prime \prime }+2\lambda x^{\prime }+\omega _{0}^{2}x=\frac{f\left ( t\right ) }{m} Where \lambda =\frac{\rho }{2m} where \rho is the damping coefficient and \omega _{0}=\sqrt{\frac{k}{m}} is the natural frequency and k is the stiffness. Using the above form, and letting F\left ( s\right ) be the Laplace transform of f\left ( t\right ) and X\left ( s\right ) the Laplace transform of the solution x\left ( t\right ) and applying the Laplace transform results in \left ( s^{2}X-sx\left ( 0\right ) -x^{\prime }\left ( 0\right ) \right ) +2\lambda \left ( sX-x\left ( 0\right ) \right ) +\omega _{0}^{2}X=\frac{1}{m}F\left ( s\right ) Applying initial conditions\begin{align} \left ( s^{2}X-v_{0}\right ) +2\lambda sX+\omega _{0}^{2}X & =\frac{1}{m}F\nonumber \\ X\left ( s^{2}+2\lambda s+\omega _{0}^{2}\right ) & =\frac{1}{m}F+v_{0}\nonumber \\ X & =\frac{1}{m}\frac{F}{s^{2}+2\lambda s+\omega _{0}^{2}}+\frac{v_{0}}{s^{2}+2\lambda s+\omega _{0}^{2}} \tag{1} \end{align}
Finding the roots of the characteristic equation s^{2}+2\lambda s+\omega ^{2} gives r=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}=-\lambda \pm \sqrt{\lambda ^{2}-\omega _{0}^{2}} Since underdamped, therefore \omega >\lambda then the quantity under the radical is negative and the roots are complex conjugate r=-\lambda \pm i\sqrt{\omega _{0}^{2}-\lambda ^{2}}=-\lambda \pm i\omega _{0}\sqrt{1-\frac{\lambda ^{2}}{\omega _{0}^{2}}}=-\frac{\rho }{2m}\pm i\omega _{0}\sqrt{1-\frac{\rho ^{2}}{4m^{2}\omega _{0}^{2}}} But \frac{\rho ^{2}}{4m^{2}\omega _{0}^{2}}=\xi ^{2} where \xi =\frac{\rho }{2m\omega _{0}} is the damping ratio. Hence the above can be written in the more common form as r=-\frac{\rho }{2m}\pm i\omega _{0}\sqrt{1-\frac{\rho ^{2}}{4m^{2}\omega ^{2}}}=-\xi \omega _{0}\pm i\omega _{0}\sqrt{1-\xi ^{2}} In addition, defining \omega _{d}=\omega _{0}\sqrt{1-\xi ^{2}} as the natural damped frequency, hence r=-\frac{\rho }{2m}\pm i\omega _{0}\sqrt{1-\xi ^{2}}=-\xi \omega _{0}\pm i\omega _{d} Let r_{1}=-\xi \omega _{0}+i\omega _{d},r_{2}=-\xi \omega _{0}-i\omega _{d}. Eq. (1) can now be written as X=\frac{1}{m}\frac{F}{\left ( s-r_{1}\right ) \left ( s-r_{2}\right ) }+\frac{v_{0}}{\left ( s-r_{1}\right ) \left ( s-r_{2}\right ) } Let \begin{align*} G\left ( s\right ) & =\frac{1}{\left ( s-r_{1}\right ) \left ( s-r_{2}\right ) }\\ & =\frac{A}{\left ( s-r_{1}\right ) }+\frac{B}{\left ( s-r_{2}\right ) } \end{align*}
Where A=\lim _{s\rightarrow r_{1}}\frac{1}{\left ( s-r_{2}\right ) }=\frac{1}{\left ( -\xi \omega _{0}+i\omega _{d}-\left ( -\xi \omega _{0}-i\omega _{d}\right ) \right ) }=\frac{1}{2i\omega _{d}} And B=\lim _{s\rightarrow r_{2}}\frac{1}{\left ( s-r_{1}\right ) }=\frac{1}{\left ( -\xi \omega _{0}-i\omega _{d}-\left ( -\xi \omega _{0}+i\omega _{d}\right ) \right ) }=\frac{1}{-2i\omega _{d}} Therefore\begin{align*} \mathcal{L}^{-1}\left ( G\left ( s\right ) \right ) & =\mathcal{L}^{-1}\left ( \frac{1}{2i\omega _{0}\sqrt{1-\xi }}\frac{1}{\left ( s-r_{1}\right ) }-\frac{1}{2i\omega _{0}\sqrt{1-\xi }}\frac{1}{\left ( s-r_{2}\right ) }\right ) \\ & =\frac{1}{2i\omega _{0}\sqrt{1-\xi }}\mathcal{L}^{-1}\left ( \frac{1}{\left ( s-r_{1}\right ) }-\frac{1}{\left ( s-r_{2}\right ) }\right ) \\ & =\frac{1}{2i\omega _{d}}\left ( e^{r_{1}t}-e^{r_{2}t}\right ) \\ & =\frac{1}{2i\omega _{d}}\left ( e^{\left ( -\xi \omega _{0}+i\omega _{d}\right ) t}-e^{\left ( -\xi \omega _{0}-i\omega _{d}\right ) t}\right ) \\ & =\frac{1}{2i\omega _{d}}\left ( e^{-\xi \omega _{0}t}e^{i\omega _{d}t}-e^{-\xi \omega _{0}t}e^{-i\omega _{d}t}\right ) \\ & =\frac{e^{-\xi \omega _{0}t}}{2i\omega _{d}}\left ( e^{i\omega _{d}t}-e^{-i\omega _{d}t}\right ) \\ & =\frac{e^{-\xi \omega _{0}t}}{2i\omega _{d}}\left ( 2i\sin \left ( \omega _{d}t\right ) \right ) \\ & =\frac{e^{-\xi \omega _{0}t}}{\omega _{d}}\sin \left ( \omega _{d}t\right ) \end{align*}
Therefore the general solution is x\left ( t\right ) =\frac{1}{m}\mathcal{L}^{-1}\left ( F\left ( s\right ) G\left ( s\right ) \right ) +v_{0}\frac{e^{-\xi \omega _{0}t}}{\omega _{d}}\sin \left ( \omega _{d}t\right ) But \mathcal{L}^{-1}\left ( F\left ( s\right ) G\left ( s\right ) \right ) =\int _{0}^{t}f\left ( t-\tau \right ) g\left ( \tau \right ) dt, hence the above becomes\begin{align*} x\left ( t\right ) & =\frac{1}{m}\int _{0}^{t}f\left ( t-\tau \right ) \left [ \overset{g\left ( \tau \right ) }{\overbrace{\frac{e^{-\xi \omega _{0}\tau }}{\omega _{d}}\sin \left ( \omega _{d}\tau \right ) }}\right ] d\tau +v_{0}\frac{e^{-\xi \omega _{0}t}}{\omega _{d}}\sin \left ( \omega _{d}t\right ) \\ & =\frac{1}{m\omega _{d}}\left [ \int _{0}^{t}f\left ( t-\tau \right ) e^{-\xi \omega _{0}\tau }\sin \left ( \omega _{d}\tau \right ) d\tau +mv_{0}e^{-\xi \omega _{0}t}\sin \left ( \omega _{d}t\right ) \right ] \end{align*}
Now the problem can be solved for different f\left ( t\right ) .
When f\left ( t\right ) =P\delta \left ( t\right ) then the solution is x\left ( t\right ) =\frac{1}{m\omega _{d}}\left [ \int _{0}^{t}P\delta \left ( t-\tau \right ) e^{-\xi \omega _{0}\tau }\sin \left ( \omega _{d}\tau \right ) d\tau +mv_{0}\frac{e^{-\xi \omega _{0}t}}{\omega _{d}}\sin \left ( \omega _{d}t\right ) \right ] But \int _{0}^{t}\delta \left ( t-\tau \right ) r\left ( \tau \right ) d\tau =r\left ( t\right ) Hence\begin{align*} x\left ( t\right ) & =\frac{1}{m\omega _{d}}\left [ Pe^{-\xi \omega _{0}t}\sin \left ( \omega _{d}t\right ) +mv_{0}e^{-\xi \omega _{0}t}\sin \left ( \omega _{d}t\right ) \right ] \\ & =\left ( P+mv_{0}\right ) \frac{e^{-\xi \omega _{0}t}}{m\omega _{d}}\sin \left ( \omega _{d}t\right ) \end{align*}
We see that the effect of having an initial velocity is to contribute an additional impulse of magnitude mv_{0}. Therefore, this response is the same to one where an impulse of amplitude \left ( P+mv_{0}\right ) instead of P was applied to the same system when all its initial conditions are zero.
To express the above solution using the terms in the original ODE, then using \xi =\frac{\rho }{2m\omega _{0}} and \omega _{d}=\omega _{0}\sqrt{1-\left ( \frac{\rho }{2m\omega _{0}}\right ) ^{2}} then the solution is x\left ( t\right ) =\left ( P+mv_{0}\right ) \frac{e^{-\frac{\rho }{2m}t}}{m\omega _{0}\sqrt{1-\left ( \frac{\rho }{2m\omega _{0}}\right ) ^{2}}}\sin \left ( \omega _{0}\sqrt{1-\left ( \frac{\rho }{2m\omega _{0}}\right ) ^{2}}t\right )
When f\left ( t\right ) =F_{0}\sin \left ( \omega t\right ) then the solution is x\left ( t\right ) =\frac{1}{m\omega _{d}}\left [ \int _{0}^{t}F_{0}\sin \left ( \omega \left ( t-\tau \right ) \right ) e^{-\xi \omega _{0}\tau }\sin \left ( \omega _{d}\tau \right ) d\tau +mv_{0}e^{-\xi \omega _{0}t}\sin \left ( \omega _{d}t\right ) \right ] The \int _{0}^{t}\sin \left ( \omega \left ( t-\tau \right ) \right ) e^{-\xi \omega _{0}\tau }\sin \left ( \omega _{d}\tau \right ) d\tau can be done be repeated use of integration by parts by starting with writing \sin \left ( \omega \left ( t-\tau \right ) \right ) =\cos \omega \tau \sin \omega t-\cos \omega t\sin \omega \tau
The final result can be found to be5 x\left ( t\right ) =e^{-\xi \omega _{0}\tau }\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +\frac{F}{m\omega _{0}^{2}}\frac{\left ( \left ( 1-r^{2}\right ) \sin \omega t-2\xi r\cos \omega t\right ) }{\left ( 1-r^{2}\right ) ^{2}+\left ( 2\xi r\right ) ^{2}} Where r=\frac{\omega }{\omega _{0}} and A=\frac{2rF\xi }{m\omega _{0}^{2}}\frac{1}{\left ( 1-r^{2}\right ) ^{2}+\left ( 2\xi r\right ) ^{2}} and B=\frac{v_{0}}{\omega _{d}}-\frac{F\left ( 1-r^{2}\right ) }{m\omega _{0}\omega _{d}}\frac{r}{\left ( 1-r^{2}\right ) ^{2}+\left ( 2\xi r\right ) ^{2}}+\frac{2rF\xi }{m\omega _{0}\omega _{d}}\frac{1}{\left ( 1-r^{2}\right ) ^{2}+\left ( 2\xi r\right ) ^{2}}
For 0<x<L and t>0 \frac{\partial u}{\partial t}-k\frac{\partial ^{2}u}{\partial x^{2}}=ae^{-\alpha t} IC u\left ( x,0\right ) =0 and BC: u\left ( 0,t\right ) =u\left ( L,t\right ) =0
Solve using convolution.
Solution:
Lower case u is used for u\left ( x,t\right ) in the time domain so to be able to use U\left ( x,s\right ) as the transform so to keep the notation simple. Now, Taking Laplace transform, using t as the corresponding independent variable for s, hence\begin{align*} \mathcal{L}\left ( \frac{\partial u\left ( x,t\right ) }{\partial t}-k\frac{\partial ^{2}u\left ( x,t\right ) }{\partial x^{2}}\right ) & =a\mathcal{L}\left ( e^{-\alpha t}\right ) \\ \left ( sU\left ( x,s\right ) -u\left ( x,0\right ) \right ) -k\frac{d^{2}U\left ( x,s\right ) }{dx^{2}} & =\frac{a}{s+\alpha }\\ sU\left ( x,s\right ) -k\frac{d^{2}U\left ( x,s\right ) }{dx^{2}} & =\frac{a}{s+\alpha } \end{align*}
Now this is a second order ODE in U\left ( x,s\right ) \frac{d^{2}U\left ( x,s\right ) }{dx^{2}}-\frac{s}{k}U\left ( x,s\right ) =\frac{-1}{k}\frac{a}{s+\alpha } To solve, it requires two boundary conditions. The boundary condition are transformed to Laplace, hence U\left ( 0,s\right ) =0 and U\left ( L,s\right ) =0. The homogenous solution is U_{h}\left ( x,s\right ) =Ae^{-\sqrt{\frac{s}{k}}x}+Be^{\sqrt{\frac{s}{k}}x} and the particular solution is (since RHS is constant) U_{p}\left ( x,s\right ) =\frac{1}{s}\frac{a}{s+\alpha } Hence the solution is \begin{align*} U\left ( x,s\right ) & =U_{h}+U_{p}\\ & =\left ( Ae^{-\sqrt{\frac{s}{k}}x}+Be^{\sqrt{\frac{s}{k}}x}\right ) +\frac{1}{s}\frac{a}{s+\alpha } \end{align*}
When x=0 \begin{equation} \frac{-1}{s}\frac{a}{s+\alpha }=\left ( A+B\right ) \tag{1} \end{equation} and when x=L\begin{equation} \frac{-1}{s}\frac{a}{s+\alpha }=\left ( Ae^{-\sqrt{\frac{s}{k}}L}+Be^{\sqrt{\frac{s}{k}}L}\right ) \tag{2} \end{equation} From (1), A=-\left ( \frac{1}{s}\frac{a}{s+\alpha }+B\right ) , hence from Eq. (2)\begin{align*} \frac{-1}{s}\frac{a}{s+\alpha } & =-\left ( \frac{1}{s}\frac{a}{s+\alpha }+B\right ) e^{-\sqrt{\frac{s}{k}}L}+Be^{\sqrt{\frac{s}{k}}L}\\ \frac{-1}{s}\frac{a}{s+\alpha } & =-\frac{1}{s}\frac{a}{s+\alpha }e^{-\sqrt{\frac{s}{k}}L}-Be^{-\sqrt{\frac{s}{k}}L}+Be^{\sqrt{\frac{s}{k}}L}\\ \frac{-1}{s}\frac{a}{s+\alpha }+\frac{1}{s}\frac{a}{s+\alpha }e^{-\sqrt{\frac{s}{k}}L} & =B\left ( e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}\right ) \\ \frac{1}{s}\frac{a}{s+\alpha }\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) & =2B\left ( \sinh \left ( \sqrt{\frac{s}{k}}L\right ) \right ) \\ B & =\frac{\frac{1}{s}\frac{a}{s+\alpha }\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\\ & =\frac{1}{s}\frac{a}{s+\alpha }\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) } \end{align*}
Therefore \begin{align*} A & =\frac{-1}{s}\frac{a}{s+\alpha }-\frac{1}{s}\frac{a}{s+\alpha }\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\\ & =\frac{1}{s}\frac{a}{s+\alpha }\left ( -1+\frac{1}{2}\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\right ) \end{align*}
And the solution is\begin{align*} U\left ( x,s\right ) & =\left ( Ae^{-\sqrt{\frac{s}{k}}x}+Be^{\sqrt{\frac{s}{k}}x}\right ) +\frac{1}{s}\frac{a}{s+\alpha }\\ & =\frac{1}{s}\frac{a}{s+\alpha }\left ( -1+\frac{1}{2}\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\right ) e^{-\sqrt{\frac{s}{k}}x}+\frac{1}{s}\frac{a}{s+\alpha }\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }e^{\sqrt{\frac{s}{k}}x}+\frac{1}{s}\frac{a}{s+\alpha }\\ & =\frac{1}{s}\frac{a}{s+\alpha }\left [ \left ( -1+\frac{1}{2}\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\right ) e^{-\sqrt{\frac{s}{k}}x}+\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }e^{\sqrt{\frac{s}{k}}x}+1\right ] \\ & =\frac{1}{s}\frac{a}{s+\alpha }\left [ -e^{-\sqrt{\frac{s}{k}}x}+1+\frac{1}{2}\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }e^{-\sqrt{\frac{s}{k}}x}+\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}-1\right ) }{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }e^{\sqrt{\frac{s}{k}}x}\right ] \\ & =\frac{1}{s}\frac{a}{s+\alpha }\left [ -e^{-\sqrt{\frac{s}{k}}x}+1+\frac{1}{2}\frac{\left ( e^{-\sqrt{\frac{s}{k}}L}e^{-\sqrt{\frac{s}{k}}x}-e^{-\sqrt{\frac{s}{k}}x}\right ) +\left ( e^{-\sqrt{\frac{s}{k}}L}e^{\sqrt{\frac{s}{k}}x}-e^{\sqrt{\frac{s}{k}}x}\right ) }{\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\right ] \\ & =\frac{1}{s}\frac{a}{s+\alpha }\left [ -e^{-\sqrt{\frac{s}{k}}x}+1+\frac{1}{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\left ( e^{-\sqrt{\frac{s}{k}}L}e^{-\sqrt{\frac{s}{k}}x}-e^{-\sqrt{\frac{s}{k}}x}+e^{-\sqrt{\frac{s}{k}}L}e^{\sqrt{\frac{s}{k}}x}-e^{\sqrt{\frac{s}{k}}x}\right ) \right ] \\ & =\frac{1}{s}\frac{a}{s+\alpha }\left [ -e^{-\sqrt{\frac{s}{k}}x}+1+\frac{1}{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\left ( e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }+e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }+-\left ( e^{-\sqrt{\frac{s}{k}}x}+e^{\sqrt{\frac{s}{k}}x}\right ) \right ) \right ] \\ & =\frac{1}{s}\frac{a}{s+\alpha }\left [ -e^{-\sqrt{\frac{s}{k}}x}+1+\frac{1}{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\left ( e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }-\left ( 2\cosh \left ( \sqrt{\frac{s}{k}}L\right ) \right ) \right ) \right ] \end{align*}
Hence \begin{align*} Y\left ( s\right ) & =\frac{1}{s}\frac{a}{s+\alpha }\left ( 1-e^{-\sqrt{\frac{s}{k}}x}+\frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }+\frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }-\frac{\cosh \left ( \sqrt{\frac{s}{k}}L\right ) }{\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }\right ) \\ & =\frac{1}{s}\frac{a}{s+\alpha }\left ( 1-e^{-\sqrt{\frac{s}{k}}x}+\frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{\left ( e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}\right ) }+\frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{\left ( e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}\right ) }-\coth \left ( \sqrt{\frac{s}{k}}L\right ) \right ) \\ & =\frac{1}{s}\frac{a}{s+\alpha }\left ( 1-e^{-\sqrt{\frac{s}{k}}x}+\frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }+\frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{2\sinh \left ( \sqrt{\frac{s}{k}}L\right ) }-\coth \left ( \sqrt{\frac{s}{k}}L\right ) \right ) \end{align*}
Now the inverse Laplace transform is found. Let G\left ( s\right ) =\frac{1}{s}\frac{a}{s+\alpha } and \begin{align*} F\left ( s\right ) & =1-e^{-\sqrt{\frac{s}{k}}x}+\frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}+\frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}-\frac{e^{\sqrt{\frac{s}{k}}L}+e^{-\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\\ & =1-e^{-\sqrt{\frac{s}{k}}x}+\frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}+\frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}-\frac{e^{\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}-\frac{e^{-\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}} \end{align*}
hence\begin{align} u\left ( x,t\right ) & =\mathcal{L}^{-1}\left ( F\left ( s\right ) G\left ( s\right ) \right ) \nonumber \\ & =\int _{0}^{t}f\left ( \tau \right ) g\left ( t-\tau \right ) d\tau \tag{3} \end{align}
Where \begin{align*} g\left ( t\right ) & =\mathcal{L}^{-1}\left ( \frac{1}{s}\frac{a}{s+\alpha }\right ) \\ & =\mathcal{L}^{-1}\left ( \frac{a}{s\alpha }-\frac{a}{\alpha \left ( s+\alpha \right ) }\right ) \\ & =\frac{a}{\alpha }-\frac{a}{\alpha }e^{-\alpha t} \end{align*}
And \begin{equation} f\left ( t\right ) =\mathcal{L}^{-1}\left ( 1-e^{-\sqrt{\frac{s}{k}}x}+\frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}+\frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}-\frac{e^{\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}-\frac{e^{-\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\right ) \tag{4} \end{equation} Note: \mathcal{L}^{-1}\left ( e^{-\sqrt{\frac{s}{k}}x}\right ) =\frac{x}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-x^{2}}{4kt}}\qquad \text{\ for}\sqrt{\frac{1}{k}}x>0 To find the inverse Laplace of \frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\,\ , dividing by e^{\sqrt{\frac{s}{k}}L}the numerator and denominator gives \frac{e^{\sqrt{\frac{s}{k}}\left ( x-2L\right ) }}{\left ( 1-e^{-2\sqrt{\frac{s}{k}}L}\right ) } Now \frac{1}{1-z}=1+z+z^{2}+\cdots by series expansion, hence the above becomes\begin{align*} \frac{e^{\sqrt{\frac{s}{k}}\left ( x-2L\right ) }}{\left ( 1-e^{-2\sqrt{\frac{s}{k}}L}\right ) } & =e^{\sqrt{\frac{s}{k}}\left ( x-2L\right ) }\left ( 1+e^{-\sqrt{\frac{s}{k}}2L}+e^{-\sqrt{\frac{s}{k}}4L}+e^{-\sqrt{\frac{s}{k}}6L}+\cdots \right ) \\ & =\left ( e^{\sqrt{\frac{s}{k}}\left ( x-2L\right ) }+e^{\sqrt{\frac{s}{k}}\left ( x-4L\right ) }+e^{\sqrt{\frac{s}{k}}\left ( x-6L\right ) }+\cdots \right ) \end{align*}
Similarly, to find Laplace of \frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\,\ ,dividing by e^{\sqrt{\frac{s}{k}}L} the numerator and denominator gives \frac{e^{-\sqrt{\frac{s}{k}}\left ( x+2L\right ) }}{\left ( 1-e^{-2\sqrt{\frac{s}{k}}L}\right ) } Now \frac{1}{1-z}=1+z+z^{2}+\cdots by series expansion, hence the above becomes\begin{align*} \frac{e^{-\sqrt{\frac{s}{k}}\left ( x+2L\right ) }}{\left ( 1-e^{-2\sqrt{\frac{s}{k}}L}\right ) } & =e^{-\sqrt{\frac{s}{k}}\left ( x+2L\right ) }\left ( 1+e^{-\sqrt{\frac{s}{k}}2L}+e^{-\sqrt{\frac{s}{k}}4L}+e^{-\sqrt{\frac{s}{k}}6L}+\cdots \right ) \\ & =e^{-\sqrt{\frac{s}{k}}\left ( x+2L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+4L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+6L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+8L\right ) }+\cdots \end{align*}
Similarly, to find Laplace of \frac{e^{\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\,\ ,dividing by e^{\sqrt{\frac{s}{k}}L} the numerator and denominator gives \frac{1}{1-e^{-2\sqrt{\frac{s}{k}}L}} Now \frac{1}{1-z}=1+z+z^{2}+\cdots by series expansion, hence the above becomes \frac{1}{1-e^{-2\sqrt{\frac{s}{k}}L}}=\left ( 1+e^{-2\sqrt{\frac{s}{k}}2L}+e^{-4\sqrt{\frac{s}{k}}L}+e^{-6\sqrt{\frac{s}{k}}L}+\cdots \right ) And to find Laplace of \frac{e^{-\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\,\ ,dividing by e^{\sqrt{\frac{s}{k}}L} the numerator and denominator gives \frac{e^{-2\sqrt{\frac{s}{k}}L}}{1-e^{-2\sqrt{\frac{s}{k}}L}} Now \frac{1}{1-z}=1+z+z^{2}+\cdots by series expansion, hence the above becomes\begin{align*} \frac{e^{-2\sqrt{\frac{s}{k}}L}}{1-e^{-2\sqrt{\frac{s}{k}}L}} & =e^{-2\sqrt{\frac{s}{k}}L}\left ( 1+e^{-2\sqrt{\frac{s}{k}}L}+e^{-4\sqrt{\frac{s}{k}}L}+e^{-6\sqrt{\frac{s}{k}}L}+\cdots \right ) \\ & =e^{-2\sqrt{\frac{s}{k}}L}+e^{-4\sqrt{\frac{s}{k}}2L}+e^{-6\sqrt{\frac{s}{k}}L}+e^{-8\sqrt{\frac{s}{k}}L}+\cdots \end{align*}
Applying all these results to Eq. (4) above\begin{align*} f\left ( t\right ) & =\mathcal{L}^{-1}\left ( 1-e^{-\sqrt{\frac{s}{k}}x}+\frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}+\frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}-\frac{e^{\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}-\frac{e^{-\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\right ) \\ & =\mathcal{L}^{-1}1-\mathcal{L}^{-1}\left ( e^{-\sqrt{\frac{s}{k}}x}\right ) \\ & +\mathcal{L}^{-1}\left ( \frac{e^{\sqrt{\frac{s}{k}}\left ( x-L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\right ) \\ & +\mathcal{L}^{-1}\left ( \frac{e^{-\sqrt{\frac{s}{k}}\left ( x+L\right ) }}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\right ) \\ & -\mathcal{L}^{-1}\left ( \frac{e^{\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\right ) \\ & -\mathcal{L}^{-1}\left ( \frac{e^{-\sqrt{\frac{s}{k}}L}}{e^{\sqrt{\frac{s}{k}}L}-e^{-\sqrt{\frac{s}{k}}L}}\right ) \end{align*}
Hence\begin{align*} f\left ( t\right ) & =\delta \left ( t\right ) -\frac{x}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-x^{2}}{4kt}}\\ & +\mathcal{L}^{-1}\left ( e^{\sqrt{\frac{s}{k}}\left ( x-2L\right ) }+e^{\sqrt{\frac{s}{k}}\left ( x-4L\right ) }+e^{\sqrt{\frac{s}{k}}\left ( x-6L\right ) }+\cdots \right ) \\ & +\mathcal{L}^{-1}\left ( e^{-\sqrt{\frac{s}{k}}\left ( x+2L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+4L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+6L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+8L\right ) }+\cdots \right ) \\ & -\mathcal{L}^{-1}\left ( 1+e^{-2\sqrt{\frac{s}{k}}L}+e^{-4\sqrt{\frac{s}{k}}L}+e^{-6\sqrt{\frac{s}{k}}L}+\cdots \right ) \\ & -\mathcal{L}^{-1}\left ( e^{-2\sqrt{\frac{s}{k}}L}+e^{-4\sqrt{\frac{s}{k}}2L}+e^{-6\sqrt{\frac{s}{k}}L}+e^{-8\sqrt{\frac{s}{k}}L}+\cdots \right ) \end{align*}
This can be written as\begin{align*} f\left ( t\right ) & =\delta \left ( t\right ) -\frac{x}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-x^{2}}{4kt}}\\ & +\mathcal{L}^{-1}\left ( e^{-\sqrt{\frac{s}{k}}\left ( 2L-x\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( 4L-x\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( 6L-x\right ) }+\cdots \right ) \\ & +\mathcal{L}^{-1}\left ( e^{-\sqrt{\frac{s}{k}}\left ( x+2L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+4L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+6L\right ) }+e^{-\sqrt{\frac{s}{k}}\left ( x+8L\right ) }+\cdots \right ) \\ & -\mathcal{L}^{-1}\left ( 1+2e^{-2\sqrt{\frac{s}{k}}L}+2e^{-4\sqrt{\frac{s}{k}}L}+2e^{-6\sqrt{\frac{s}{k}}L}+2e^{-8\sqrt{\frac{s}{k}}L}+\cdots \right ) \end{align*}
Hence the result becomes\begin{align*} f\left ( t\right ) & =\delta \left ( t\right ) -\frac{x}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-x^{2}}{4kt}}\\ + & \frac{\left ( 2L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 2L-x\right ) ^{2}}{4kt}}+\frac{\left ( 4L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 4L-x\right ) ^{2}}{4kt}}+\frac{\left ( 6L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 6L-x\right ) ^{2}}{4kt}}+\cdots \\ + & \frac{\left ( x+2L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+2L\right ) ^{2}}{4kt}}+\frac{\left ( x+4L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+4L\right ) ^{2}}{4kt}}+\frac{\left ( x+6L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+6L\right ) ^{2}}{4kt}}+\cdots \\ & -\delta \left ( t\right ) -\frac{2L}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 2L\right ) ^{2}}{4kt}}-\frac{\left ( 4L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 4L\right ) ^{2}}{4kt}}-\frac{\left ( 6L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 6L\right ) ^{2}}{4kt}}-\cdots \\ & \cdots \end{align*}
Hence\begin{align*} f\left ( t\right ) & =-\frac{x}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-x^{2}}{4kt}}\\ & +\frac{\left ( 2L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 2L-x\right ) ^{2}}{4kt}}+\frac{\left ( 4L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 4L-x\right ) ^{2}}{4kt}}+\frac{\left ( 6L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 6L-x\right ) ^{2}}{4kt}}+\cdots \\ & +\frac{\left ( x+2L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+2L\right ) ^{2}}{4kt}}+\frac{\left ( x+4L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+4L\right ) ^{2}}{4kt}}+\frac{\left ( x+6L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+6L\right ) ^{2}}{4kt}}+\cdots \\ & -\frac{2L}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 2L\right ) ^{2}}{4kt}}-\frac{\left ( 4L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 4L\right ) ^{2}}{4kt}}-\frac{\left ( 6L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 6L\right ) ^{2}}{4kt}}-\cdots \end{align*}
Now convolution can be carried out. From Eq. (3)\begin{align*} u\left ( x,t\right ) & =\int _{0}^{t}f\left ( \tau \right ) g\left ( t-\tau \right ) d\tau \\ & =\int _{0}^{t}f\left ( \tau \right ) \left ( \frac{a}{\alpha }-\frac{a}{\alpha }e^{-\alpha \left ( t-\tau \right ) }\right ) d\tau \\ & =\frac{a}{\alpha }\left ( \int _{0}^{t}f\left ( \tau \right ) d\tau -\int _{0}^{t}f\left ( \tau \right ) e^{-\alpha \left ( t-\tau \right ) }d\tau \right ) \end{align*}
Now \begin{align*} \int _{0}^{t}f\left ( \tau \right ) d\tau & =\int _{0}^{t}-\frac{x}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-x^{2}}{4kt}}++\frac{\left ( 2L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 2L-x\right ) ^{2}}{4kt}}+\frac{\left ( 4L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 4L-x\right ) ^{2}}{4kt}}+\frac{\left ( 6L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 6L-x\right ) ^{2}}{4kt}}+\cdots \\ & +\frac{\left ( x+2L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+2L\right ) ^{2}}{4kt}}+\frac{\left ( x+4L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+4L\right ) ^{2}}{4kt}}+\frac{\left ( x+6L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( x+6L\right ) ^{2}}{4kt}}+\cdots \\ & -\frac{2L}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 2L\right ) ^{2}}{4kt}}-\frac{\left ( 4L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 4L\right ) ^{2}}{4kt}}-\frac{\left ( 6L\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 6L\right ) ^{2}}{4kt}}-\cdots \end{align*}
and \int _{0}^{t}f\left ( \tau \right ) e^{-\alpha \left ( t-\tau \right ) }d\tau =\int _{0}^{t}\left ( -\frac{x}{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-x^{2}}{4kt}}+\frac{\left ( 2L-x\right ) }{2\sqrt{\pi k}}\frac{1}{t^{\frac{3}{2}}}e^{\frac{-\left ( 2L-x\right ) ^{2}}{4kt}}+\cdots \right ) e^{-\alpha \left ( t-\tau \right ) }d\tau The last 2 integral, when evaluated give the solution u\left ( x,t\right )