Find Fourier expansion of the periodic function whose definition on one period is\[ f\left ( t\right ) =\left \{ \begin{array} [c]{ccc}t & & 0<t<2\\ 4-t & & 2<t<4 \end{array} \right . \]
Solution:
The function \(f\left ( t\right ) \) is (for 3 periods)
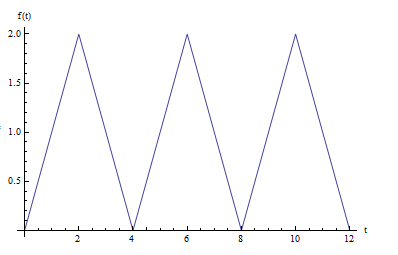
The period is \(T=4\). Let Fourier series approximation of \(f\left ( t\right ) \) be \(\tilde{f}\left ( t\right ) \), hence from the definition\[ \tilde{f}\left ( t\right ) =\frac{a_{0}}{2}+\sum _{n=1}^{\infty }a_{n}\cos \left ( \frac{2\pi }{T}nt\right ) +b_{n}\sin \left ( \frac{2\pi }{T}nt\right ) \] This is an even function, hence \(b_{n}=0\) and only \(a_{n}\) needs to be found. Hence\[ \tilde{f}\left ( t\right ) =\frac{a_{0}}{2}+\sum _{n=1}^{\infty }a_{n}\cos \left ( \frac{2\pi }{T}nt\right ) \]\begin{align*} a_{0} & =\frac{1}{T/2}\int _{0}^{T}f\left ( t\right ) dt=\frac{1}{2}\left ( \int _{0}^{2}tdt+\int _{2}^{4}\left ( 4-t\right ) dt\right ) \\ & =\frac{1}{2}\left ( \left [ \frac{t^{2}}{2}\right ] _{0}^{2}+\left [ 4t-\frac{t^{2}}{^{2}}\right ] _{2}^{4}\right ) =\frac{1}{2}\left ( 2+\left ( 16-\frac{16}{^{2}}\right ) -\left ( 8-\frac{4}{^{2}}\right ) \right ) \\ & =\frac{1}{2}\left ( 2+8-6\right ) \\ & =2 \end{align*}
And\[ a_{n}=\frac{1}{T/2}\int _{0}^{T}\cos \left ( \frac{2\pi }{T}nt\right ) f\left ( t\right ) dt=\frac{1}{2}\left ( \int _{0}^{2}t\cos \left ( \frac{2\pi }{T}nt\right ) dt+\int _{2}^{4}\left ( 4-t\right ) \cos \left ( \frac{2\pi }{T}nt\right ) dt\right ) \] But \(T=4\), hence the above simplifies to\[ a_{n}=\frac{8\sin ^{2}\left ( \frac{\pi n}{2}\right ) \cos \left ( \pi n\right ) }{\pi ^{2}n^{2}}\] Looking at few terms\begin{align*} a_{n} & =8\left \{ \frac{\sin ^{2}\left ( \frac{\pi }{2}\right ) \cos \left ( \pi \right ) }{\pi ^{2}},\frac{\sin ^{2}\left ( \pi \right ) \cos \left ( 2\pi \right ) }{\pi ^{2}2^{2}},\frac{\sin ^{2}\left ( \frac{3\pi }{2}\right ) \cos \left ( 3\pi \right ) }{\pi ^{2}3^{2}},\frac{\sin ^{2}\left ( 2\pi \right ) \cos \left ( 4\pi \right ) }{\pi ^{2}4^{2}},\cdots \right \} \\ & =8\left \{ \frac{\cos \left ( \pi \right ) }{\pi ^{2}},0,\frac{\cos \left ( 3\pi \right ) }{\pi ^{2}3^{2}},0,\frac{\cos \left ( 5\pi \right ) }{\pi ^{2}5^{2}},\cdots \right \} \\ & =8\left \{ \frac{-1}{\pi ^{2}},0,\frac{-1}{\pi ^{2}3^{2}},0,\frac{-1}{\pi ^{2}5^{2}},\cdots \right \} \end{align*}
Hence \[ a_{n}=\frac{-8}{\pi ^{2}n^{2}}\qquad n=1,3,5,\cdots \] Therefore\begin{align*} \tilde{f}\left ( t\right ) & =\frac{a_{0}}{2}+\sum _{n=1}^{\infty }a_{n}\cos \left ( \frac{2\pi }{T}nt\right ) \\ & =1-\frac{8}{\pi ^{2}}\sum _{n=1,3,5,\cdots }^{\infty }\frac{1}{n^{2}}\cos \left ( \frac{\pi }{2}nt\right ) \end{align*}
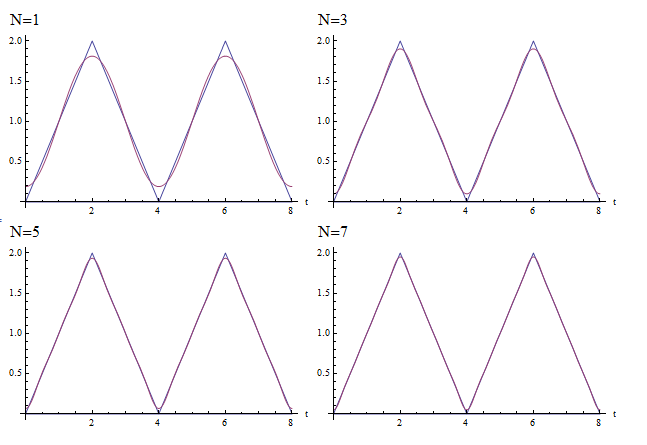
This is a plot of \(\tilde{f}\left ( t\right ) \) showing the approximation as \(n\) is increased for few terms. Sum needed to go to only \(n=7\) to obtain a very good approximation.
Find the complex exponential Fourier series of the periodic function whose definition on one period is \(f\left ( t\right ) =\cosh \left ( t\right ) ;-1<t<1\)
Solution:
The period is \(T=2\). Let Fourier series approximation of \(f\left ( t\right ) \) be \(\tilde{f}\left ( t\right ) \), hence from the definition\begin{align*} \tilde{f}\left ( t\right ) & =\sum _{n=-\infty }^{\infty }c_{n}e^{i\frac{2\pi }{T}nt}\\ c_{n} & =\frac{1}{T}\int _{-\frac{T}{2}}^{\frac{T}{2}}f\left ( t\right ) e^{-i\frac{2\pi }{T}nt}dt\qquad n=0,\pm 1,\pm 2,\cdots \end{align*}
Hence\begin{align*} c_{n} & =\frac{1}{2}\int _{-1}^{1}\cosh \left ( t\right ) e^{-i\frac{2\pi }{T}nt}dt\\ & =\frac{1}{2}\int _{-1}^{1}\cosh \left ( t\right ) e^{-i\pi nt}dt\\ & =\frac{1}{2}\int _{-1}^{1}\left ( \frac{e^{-t}}{2}+\frac{e^{t}}{2}\right ) e^{-i\pi nt}dt\\ & =\frac{1}{4}\left ( \int _{-1}^{1}e^{\left ( -i\pi n-1\right ) t}dt+\int _{-1}^{1}e^{\left ( -i\pi n+1\right ) t}dt\right ) \\ & =\frac{1}{4}\left ( \left [ \frac{e^{\left ( -i\pi n-1\right ) t}}{-i\pi n-1}\right ] _{-1}^{1}+\left [ \frac{e^{\left ( -i\pi n+1\right ) t}}{-i\pi n+1}\right ] _{-1}^{1}\right ) \\ & =\frac{1}{4}\left ( \frac{e^{\left ( -i\pi n-1\right ) }-e^{\left ( i\pi n+1\right ) }}{-i\pi n-1}+\frac{e^{\left ( -i\pi n+1\right ) }-e^{\left ( i\pi n-1\right ) }}{-i\pi n+1}\right ) \\ & =\frac{1}{4}\left ( \frac{\left ( -i\pi n+1\right ) e^{\left ( -i\pi n-1\right ) }-\left ( -i\pi n+1\right ) e^{\left ( i\pi n+1\right ) }+\left ( -i\pi n-1\right ) e^{\left ( -i\pi n+1\right ) }-\left ( -i\pi n-1\right ) e^{\left ( i\pi n-1\right ) }}{\left ( -i\pi n-1\right ) \left ( -i\pi n+1\right ) }\right ) \\ & =\frac{1}{4}\left ( \frac{-i\pi ne^{\left ( -i\pi n-1\right ) }+e^{\left ( -i\pi n-1\right ) }+i\pi ne^{\left ( i\pi n+1\right ) }-e^{\left ( i\pi n+1\right ) }-i\pi ne^{\left ( -i\pi n+1\right ) }-e^{\left ( -i\pi n+1\right ) }+i\pi ne^{\left ( i\pi n-1\right ) }+e^{\left ( i\pi n-1\right ) }}{-\pi ^{2}n^{2}-1}\right ) \\ & =\frac{1}{4}\left ( \frac{-i\pi ne^{\left ( -i\pi n-1\right ) }+e^{\left ( -i\pi n-1\right ) }+i\pi ne^{\left ( i\pi n+1\right ) }-e^{\left ( i\pi n+1\right ) }-i\pi ne^{\left ( -i\pi n+1\right ) }-e^{\left ( -i\pi n+1\right ) }+i\pi ne^{\left ( i\pi n-1\right ) }+e^{\left ( i\pi n-1\right ) }}{-\pi ^{2}n^{2}-1}\right ) \end{align*}
Collect terms\begin{align*} c_{n} & =\frac{1}{4}\left ( \frac{-i\pi nee^{-i\pi n}+e^{-1}e^{-i\pi n}+i\pi nee^{i\pi n}-ee^{i\pi n}-i\pi ne^{-i\pi n}-ee^{-i\pi n}+i\pi ne^{-1}e^{i\pi n}+e^{-1}e^{-i\pi n}}{-\pi ^{2}n^{2}-1}\right ) \\ & =\frac{1}{4}\left ( \frac{e^{-1}e^{-i\pi n}(-i\pi n+1+i\pi n+1)+ee^{i\pi n}\left ( in\pi -1-i\pi n-1\right ) }{-\pi ^{2}n^{2}-1}\right ) \\ & =\frac{1}{4}\left ( \frac{2e^{-1}e^{-i\pi n}-2ee^{i\pi n}}{-\pi ^{2}n^{2}-1}\right ) \\ & =\frac{1}{2}\left ( \frac{e^{-1}\left ( \cos n\pi -i\sin n\pi \right ) -e\left ( \cos n\pi +i\sin n\pi \right ) }{-\pi ^{2}n^{2}-1}\right ) \end{align*}
But \(n\) is an integer therefore \(\sin n\pi =0\)\begin{align*} c_{n} & =\frac{1}{2}\left ( \frac{e^{-1}\cos n\pi -e\cos n\pi }{-\pi ^{2}n^{2}-1}\right ) \\ & =\frac{1}{2}\left ( \frac{\cos n\pi \left ( 1-e^{2}\right ) }{e\left ( -\pi ^{2}n^{2}-1\right ) }\right ) \\ & =\frac{1}{2e}\left ( \frac{\cos n\pi \left ( e^{2}-1\right ) }{1+\pi ^{2}n^{2}}\right ) \end{align*}
Looking at few terms\begin{align*} c_{n} & =\left \{ \overbrace{\frac{1}{2e}\left ( \frac{\cos \left ( -\pi \right ) \left ( e^{2}-1\right ) }{1+\pi ^{2}}\right ) }^{n=-1} ,\overbrace{\frac{1}{2e}\left ( \frac{\cos \left ( 0\right ) \left ( e^{2}-1\right ) }{1+\pi ^{2}}\right ) }^{n=0},\overset{n=1}{\overbrace{\frac{1}{2e}\left ( \frac{\cos \pi \left ( e^{2}-1\right ) }{1+\pi ^{2}}\right ) }},\overbrace{\frac{1}{2e}\left ( \frac{\cos 2\pi \left ( e^{2}-1\right ) }{1+\pi ^{2}2^{2}}\right ) }^{n=2},\cdots \right \} \\ & =\left \{ \frac{1}{2e}\left ( \frac{-1\left ( e^{2}-1\right ) }{1+\pi ^{2}}\right ) ,\frac{1}{2e}\left ( \frac{\left ( e^{2}-1\right ) }{1+\pi ^{2}}\right ) ,\frac{1}{2e}\left ( \frac{-1\left ( e^{2}-1\right ) }{1+\pi ^{2}}\right ) ,\frac{1}{2e}\left ( \frac{\left ( e^{2}-1\right ) }{1+\pi ^{2}2^{2}}\right ) ,\frac{1}{2e}\left ( \frac{-1\left ( e^{2}-1\right ) }{1+\pi ^{2}3^{2}}\right ) ,\cdots \right \} \end{align*}
Hence\begin{align*} c_{n} & =\left ( -1\right ) ^{\left \vert n\right \vert }\frac{\left ( e^{2}-1\right ) }{2e\left ( 1+\pi ^{2}n^{2}\right ) }\qquad n=\pm 1,\pm 2,\cdots \\ & =\frac{\left ( e^{2}-1\right ) }{2e}\qquad n=0 \end{align*}
The first few terms are\[ -0.108118,0.02903,-0.013083,0.0073952,\cdots \} \] Hence\begin{align*} \tilde{f}\left ( t\right ) & =\sum _{n=-\infty }^{\infty }c_{n}e^{i\frac{2\pi }{T}nt}\\ & =\frac{\left ( e^{2}-1\right ) }{2e}+\frac{\left ( e^{2}-1\right ) }{2e}\sum _{\substack{n=-\infty \\n\neq 0}}^{\infty }\frac{\left ( -1\right ) ^{\left \vert n\right \vert }}{\left ( 1+\pi ^{2}n^{2}\right ) }e^{i\pi nt}\\ & =\frac{\left ( e^{2}-1\right ) }{2e}\left ( 1+\sum _{n=1}^{\infty }\frac{\left ( -1\right ) ^{n}}{\left ( 1+\pi ^{2}n^{2}\right ) }\left ( e^{i\pi nt}+e^{-i\pi nt}\right ) \right ) \\ & =\frac{\left ( e^{2}-1\right ) }{2e}\left ( 1+\sum _{n=1}^{\infty }\frac{\left ( -1\right ) ^{n}}{\left ( 1+\pi ^{2}n^{2}\right ) }\left ( 2\cos \left ( \pi nt\right ) \right ) \right ) \\ & =\frac{\left ( e^{2}-1\right ) }{2e}\left ( 1+2\sum _{n=1}^{\infty }\frac{\left ( -1\right ) ^{n}}{\left ( 1+\pi ^{2}n^{2}\right ) }\cos \left ( \pi nt\right ) \right ) \end{align*}
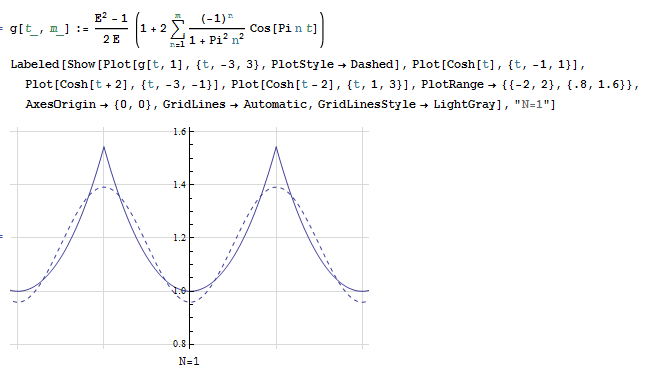
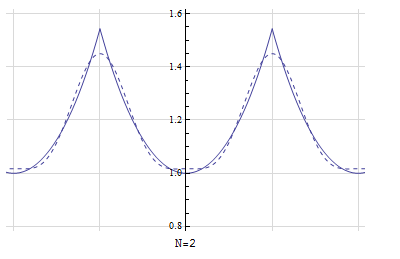
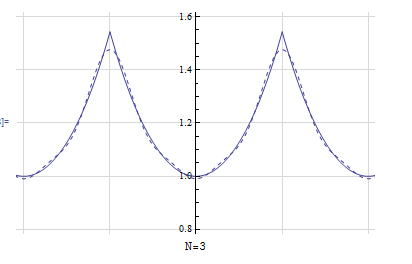
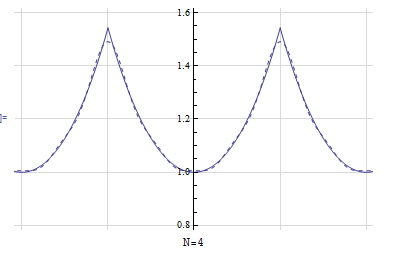
Here is a plot of the function, and its approximation \(\tilde{f}\left ( t\right ) \) for few terms. This shows the convergence is rapid and at \(N=4\) it was very close to the original periodic function

Since the D.E. is constant coefficients, then the homogeneous solution is found from the roots of the characteristic equations. The roots are \(\lambda =\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}=\frac{3\pm \sqrt{9-\left ( 4\right ) \left ( 2\right ) }}{2}=\frac{3\pm 1}{2}\), hence \(\lambda _{1}=2,\lambda _{2}=1\) and the homogeneous solution is
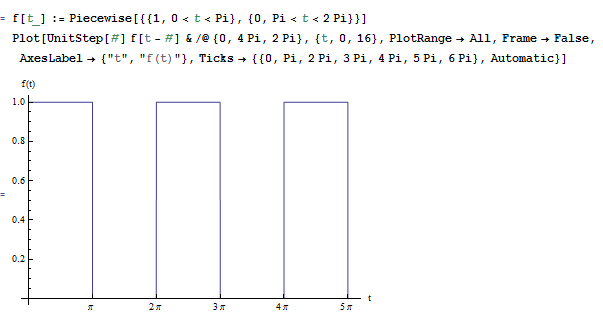
\[ y_{h}=Ae^{2t}+Be^{t}\] To find the particular solution, \(f\left ( t\right ) \) is first expressed in its Fourier series approximation form. A plot of \(f\left ( t\right ) \) is (assuming it is periodic) shows the period is \(T=2\pi \)
For \(n=0\)\begin{align*} c_{0} & =\frac{1}{T}\int _{-\frac{T}{2}}^{\frac{T}{2}}f\left ( t\right ) dt\qquad \\ & =\frac{1}{2\pi }\int _{0}^{\pi }dt\\ & =\frac{1}{2} \end{align*}
For all other values of \(n\)\begin{align*} c_{n} & =\frac{1}{2\pi }\left ( \int _{0}^{\pi }1\times e^{-i\frac{2\pi }{T}nt}dt+\int _{\pi }^{2\pi }0\times e^{-i\frac{2\pi }{T}nt}dt\right ) \\ & =\frac{1}{2\pi }\int _{0}^{\pi }e^{-int}dt\\ & =\frac{1}{2\pi }\left [ \frac{e^{-int}}{-in}\right ] _{0}^{\pi }=\frac{i}{2\pi n}\left [ e^{-int}\right ] _{0}^{\pi }\\ & =\frac{i}{2\pi n}\left ( e^{-in\pi }-1\right ) \\ & =\left ( \frac{1}{\pi }\right ) \left ( \frac{1}{2i}\right ) \left ( \frac{1}{n}\right ) \left ( 1-e^{-in\pi }\right ) \end{align*}
But \(1-e^{-in\pi }=1-\left ( -1\right ) ^{n}\) which is zero for \(n\) even and \(2\) for \(n\) odd, Hence\begin{align*} \tilde{f}\left ( t\right ) & =\frac{1}{2}+\sum _{\substack{n=-\infty \\n\neq 0}}^{\infty }c_{n}e^{int}\\ & =\frac{1}{2}+\sum _{\substack{n=-\infty \\n\text{ odd}\\n\neq 0}}^{\infty }\left ( \frac{2}{\pi }\right ) \left ( \frac{1}{2i}\right ) \left ( \frac{1}{n}\right ) e^{int} \end{align*}
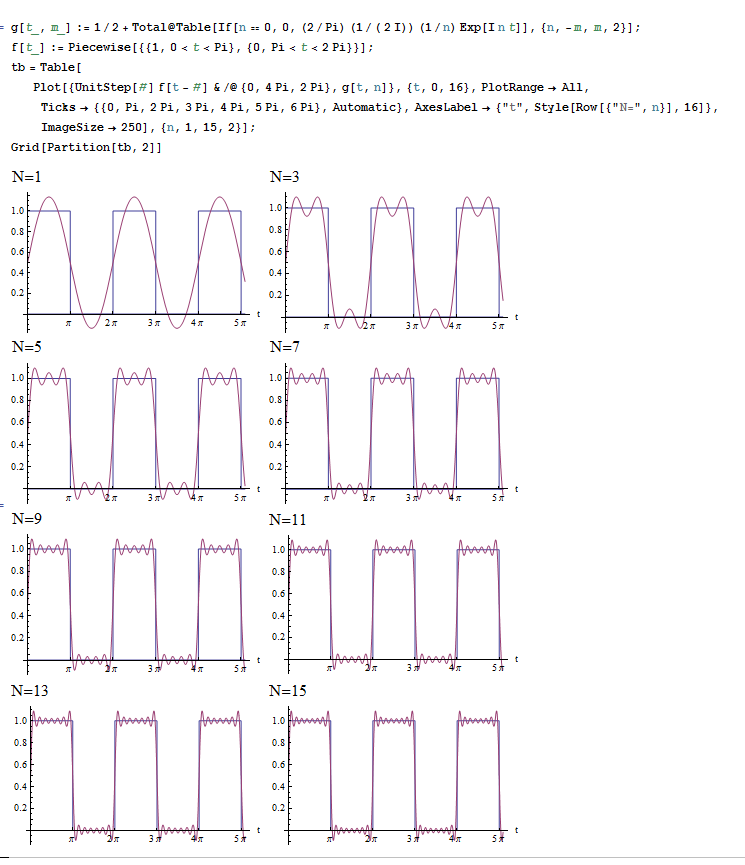
This is a plot of \(\tilde{f}\left ( t\right ) \) showing the approximation as \(n\) is increased for few terms.
Now \(c_{n}\) needs to be found. The D.E. becomes\begin{align*} y_{p}^{\prime \prime }-3y_{p}^{\prime }+2y_{p} & =\frac{1}{2}+\sum _{\substack{n=-\infty \\n\text{ odd}\\n\neq 0}}^{\infty }\left ( \frac{2}{\pi }\right ) \left ( \frac{1}{2i}\right ) \left ( \frac{1}{n}\right ) e^{int}\\ \sum _{n=-\infty }^{\infty }-n^{2}c_{n}e^{int}-3\sum _{n=-\infty }^{\infty }inc_{n}e^{int}+2\sum _{n=-\infty }^{\infty }c_{n}e^{int} & =\frac{1}{2}+\sum _{\substack{n=-\infty \\n\text{ odd}\\n\neq 0}}^{\infty }\left ( \frac{2}{\pi }\right ) \left ( \frac{1}{2i}\right ) \left ( \frac{1}{n}\right ) e^{int}\\ \sum _{n=-\infty }^{\infty }\left ( -n^{2}-3in+2\right ) c_{n}e^{int} & =\frac{1}{2}+\sum _{\substack{n=-\infty \\n\text{ odd}\\n\neq 0}}^{\infty }\left ( \frac{2}{\pi }\right ) \left ( \frac{1}{2i}\right ) \left ( \frac{1}{n}\right ) e^{int}\\ 2c_{0}+\sum _{\substack{n=-\infty \\n\neq 0}}^{\infty }\left ( -n^{2}-3in+2\right ) c_{n}e^{int} & =\frac{1}{2}+\sum _{\substack{n=-\infty \\n\text{ odd}\\n\neq 0}}^{\infty }\left ( \frac{2}{\pi }\right ) \left ( \frac{1}{2i}\right ) \left ( \frac{1}{n}\right ) e^{int} \end{align*}
Therefore, by comparing\[ c_{0}=\frac{1}{4}\] And then rest of the terms are given by\begin{align*} \sum _{\substack{n=-\infty \\n\neq 0}}^{\infty }\left ( -n^{2}-3in+2\right ) c_{n} & =\sum _{\substack{n=-\infty \\n\text{ odd}\\n\neq 0}}^{\infty }\left ( \frac{2}{\pi }\right ) \left ( \frac{1}{2i}\right ) \left ( \frac{1}{n}\right ) \\ c_{n} & =\frac{\left ( \frac{2}{\pi }\right ) \left ( \frac{1}{2i}\right ) \left ( \frac{1}{n}\right ) }{-n^{2}-3in+2}\qquad n\text{ odd,}n\neq 0\\ & =\frac{2}{\pi }\left ( \frac{1}{2i}\right ) \frac{1}{-n^{3}-3in^{2}+2n}\qquad n\text{ odd,}n\neq 0 \end{align*}
Therefore, \[ y_{p}=\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=-\infty \\n\text{ odd}\\n\neq 0}}^{\infty }\frac{1}{-n^{3}-3in^{2}+2n}\left ( \frac{1}{2i}\right ) e^{int}\] The above is converted to a sum from \(1\) to infinity. The first step is to break it into 2 sums\[ y_{p}=\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=-\infty \\odd}}^{-1}\frac{1}{-n^{3}-3in^{2}+2n}\left ( \frac{1}{2i}\right ) e^{int}+\sum _{\substack{n=1\\odd}}^{\infty }\frac{1}{-n^{3}-3in^{2}+2n}\left ( \frac{1}{2i}\right ) e^{int}\] To take care of the \(odd\) part of the sum, for the \(\sum _{\substack{n=-\infty }}^{-1}\) part, let \(n=2m+1\) and the \(\sum _{n=1}^{\infty }\) part of the sum let \(n=2m-1\). The above becomes\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=-\infty }}^{-1}\frac{1}{-\left ( 2m+1\right ) ^{3}-3i\left ( 2m+1\right ) ^{2}+2\left ( 2m+1\right ) }\left ( \frac{1}{2i}\right ) e^{i\left ( 2m+1\right ) t}\\ & +\frac{2}{\pi }\sum _{m=1}^{\infty }\frac{1}{-\left ( 2m-1\right ) ^{3}-3i\left ( 2m-1\right ) ^{2}+2\left ( 2m-1\right ) }\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t} \end{align*}
\(\sum _{\substack{m=-\infty }}^{-1}\) is changed to \(\sum _{\substack{m=\infty }}^{1}\) by replacing \(m\) with \(-m\) in the first sum above, giving\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=\infty }}^{1}\frac{1}{-\left ( 2\left ( -m\right ) +1\right ) ^{3}-3i\left ( 2\left ( -m\right ) +1\right ) ^{2}+2\left ( 2\left ( -m\right ) +1\right ) }\left ( \frac{1}{2i}\right ) e^{i\left ( 2\left ( -m\right ) +1\right ) t}\\ & +\frac{2}{\pi }\sum _{m=1}^{\infty }\frac{1}{-\left ( 2m-1\right ) ^{3}-3i\left ( 2m-1\right ) ^{2}+2\left ( 2m-1\right ) }\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t} \end{align*}
Simplifying by extracting a minus from the first sum to make all terms the same as the second sum\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{1}{-\left ( -\left ( 2m-1\right ) \right ) ^{3}-3i\left ( -\left ( 2m-1\right ) \right ) ^{2}+2\left ( -\left ( 2m-1\right ) \right ) }\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}\\ & +\frac{2}{\pi }\sum _{m=1}^{\infty }\frac{1}{-\left ( 2m-1\right ) ^{3}-3i\left ( 2m-1\right ) ^{2}+2\left ( 2m-1\right ) }\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t} \end{align*}
Or\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{1}{\left ( 2m-1\right ) ^{3}-3i\left ( 2m-1\right ) ^{2}-2\left ( 2m-1\right ) }\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}\\ & +\frac{2}{\pi }\sum _{m=1}^{\infty }\frac{1}{-\left ( 2m-1\right ) ^{3}-3i\left ( 2m-1\right ) ^{2}+2\left ( 2m-1\right ) }\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t} \end{align*}
To simplify this more, let \(\left ( 2m-1\right ) ^{3}=A,3\left ( 2m-1\right ) ^{2}=B,2\left ( 2m-1\right ) =C\,\), hence the above becomes\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{1}{A-Bi-C}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}+\frac{1}{-A-Bi+C}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t}\\ & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{1}{\left ( A-C\right ) -Bi}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}+\frac{1}{-\left ( A-C\right ) -Bi}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t}\\ & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{1}{\left ( A-C\right ) -Bi}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}-\frac{1}{\left ( A-C\right ) +Bi}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t} \end{align*}
Let \(A-C=D\) then\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\left ( \sum _{\substack{m=1}}^{\infty }\frac{1}{D-Bi}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}-\frac{1}{D+Bi}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t}\right ) \\ & =\frac{1}{4}+\frac{2}{\pi }\left ( \sum _{\substack{m=1}}^{\infty }\frac{1}{D-Bi}\frac{D+Bi}{D+Bi}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}-\frac{1}{D+Bi}\frac{D-Bi}{D-Bi}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t}\right ) \\ & =\frac{1}{4}+\frac{2}{\pi }\left ( \sum _{\substack{m=1}}^{\infty }\frac{D+Bi}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}-\frac{D-Bi}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t}\right ) \\ & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{D+Bi}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}-\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{D-Bi}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t}\\ & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{D}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{Bi}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) e^{-i\left ( 2m-1\right ) t}\\ & -\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{D}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{Bi}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) e^{i\left ( 2m-1\right ) t} \end{align*}
Now common terms can be combined\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{D}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) \left ( e^{-i\left ( 2m-1\right ) t}-e^{i\left ( 2m-1\right ) t}\right ) \\ & +\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{Bi}{B^{2}+D^{2}}\left ( \frac{1}{2i}\right ) \left ( e^{-i\left ( 2m-1\right ) t}+e^{i\left ( 2m-1\right ) t}\right ) \end{align*}
Hence\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{-D}{B^{2}+D^{2}}\sin \left ( nt\right ) +\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{B}{B^{2}+D^{2}}\cos \left ( nt\right ) \\ & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{m=1}}^{\infty }\frac{B}{B^{2}+D^{2}}\cos \left ( nt\right ) -\frac{D}{B^{2}+D^{2}}\sin \left ( nt\right ) \end{align*}
Replacing back values for \(B\) and \(D.\) Since \(D=A-C=\left ( 2n-1\right ) ^{3}-2\left ( 2n-1\right ) =\allowbreak 8n^{3}-12n^{2}+2n+1\) and \(B=3\left ( 2n-1\right ) ^{2}\), therefore\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{3\left ( 2n-1\right ) ^{2}}{9\left ( 2n-1\right ) ^{4}+\left ( \left ( 2n-1\right ) ^{3}-2\left ( 2n-1\right ) \right ) ^{2}}\cos \left ( nt\right ) \\ & -\frac{\left ( 2n-1\right ) ^{3}-2\left ( 2n-1\right ) }{9\left ( 2n-1\right ) ^{4}+\left ( \left ( 2n-1\right ) ^{3}-2\left ( 2n-1\right ) \right ) ^{2}}\sin \left ( nt\right ) \end{align*}
or\begin{align*} y_{p} & =\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{3}{16n^{4}-32n^{3}+44n^{2}-28n+10}\cos \left ( nt\right ) \\ & +\frac{-4n^{2}+4n+1}{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10}\sin \left ( nt\right ) \end{align*}
And the solution is\[ y=Ae^{2t}+Be^{t}+y_{p}\] When \(t=0\);\(y=0\) hence\begin{equation} 0=A+B+\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{3}{16n^{4}-32n^{3}+44n^{2}-28n+10} \tag{1} \end{equation} Taking derivative\begin{align*} y^{\prime } & =2Ae^{2t}+Be^{t}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{-3n\sin \left ( nt\right ) }{16n^{4}-32n^{3}+44n^{2}-28n+10}\\ & +\frac{\left ( -4n^{2}+4n+1\right ) n\cos \left ( nt\right ) }{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10} \end{align*}
When \(t=0,y^{\prime }=0\) hence\begin{equation} 0=2A+B+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{\left ( -4n^{2}+4n+1\right ) n}{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10} \tag{2} \end{equation} Subtract Eq. (1) from Eq. (2) gives\begin{align*} 0 & =A+-\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{\left ( -4n^{2}+4n+1\right ) n}{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10}\\ & -\frac{3}{16n^{4}-32n^{3}+44n^{2}-28n+10}\\ A & =\frac{1}{4}-\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{\left ( -4n^{2}+4n+1\right ) n}{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10}-\frac{3}{16n^{4}-32n^{3}+44n^{2}-28n+10}\\ & =\frac{1}{4}-\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{-4n^{3}+4n^{2}-5n+3}{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10} \end{align*}
And from Eq. (1), \(B\) can now be found\begin{align*} B & =-A-\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{3}{16n^{4}-32n^{3}+44n^{2}-28n+10}\\ & =-\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{-4n^{3}+4n^{2}-5n+3}{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10}\\ & -\frac{1}{4}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{3}{16n^{4}-32n^{3}+44n^{2}-28n+10}\\ B & =-\frac{1}{2}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{-4n^{3}+4n^{2}-5n+3}{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10}+\frac{3}{16n^{4}-32n^{3}+44n^{2}-28n+10}\\ & =-\frac{1}{2}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{1}{2}n\frac{-4n^{2}+4n+1}{16n^{5}-40n^{4}+60n^{3}-50n^{2}+24n-5} \end{align*}
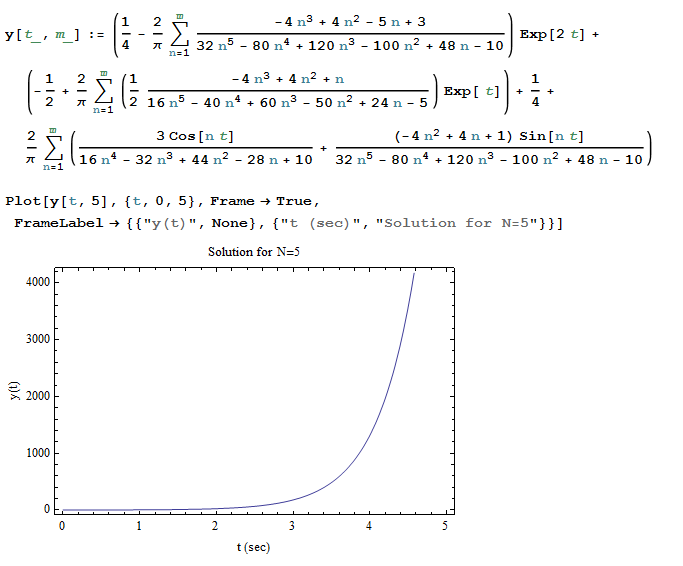
Hence the solution is\begin{align*} y & =Ae^{2t}+Be^{t}+y_{p}t\\ & =\left ( \frac{1}{4}-\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{-4n^{3}+4n^{2}-5n+3}{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10}\right ) e^{2t}\\ & +\left ( -\frac{1}{2}+\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\frac{1}{2}\frac{-4n^{3}+4n^{2}+n}{16n^{5}-40n^{4}+60n^{3}-50n^{2}+24n-5}\right ) e^{t}\\ & +\frac{1}{4}\\ & +\frac{2}{\pi }\sum _{\substack{n=1}}^{\infty }\left ( \frac{3\cos \left ( nt\right ) }{16n^{4}-32n^{3}+44n^{2}-28n+10}+\frac{\left ( -4n^{2}+4n+1\right ) \sin \left ( nt\right ) }{32n^{5}-80n^{4}+120n^{3}-100n^{2}+48n-10}\right ) \end{align*}
This is a plot of the solution for \(n=4\). Notice that the system as given is unstable. This is because the damping is negative. Hence the solution below blows up. I think the ODE should have been \(y^{\prime \prime }+3y+2y=f\left ( t\right ) \) and not \(y^{\prime \prime }-3y+2y=f\left ( t\right ) \). May be a typo. But here is the solution plot
The Fourier series approximation using the classical definition can be obtained as follows\[ \tilde{f}\left ( t\right ) =\frac{a_{0}}{2}+\sum _{n=1}^{\infty }a_{n}\cos \left ( \frac{2\pi }{T}nt\right ) +b_{n}\sin \left ( \frac{2\pi }{T}nt\right ) \] Where\begin{align*} a_{0} & =\frac{1}{T/2}\int _{0}^{T}f\left ( t\right ) dt=\frac{1}{\pi }\left ( \int _{0}^{\pi }dt+\int _{\pi }^{2\pi }0dt\right ) \\ & =1 \end{align*}
And\[ a_{n}=\frac{1}{\pi }\int _{0}^{\pi }\cos \left ( \frac{2\pi }{T}nt\right ) dt=\frac{1}{\pi }\int _{0}^{\pi }\cos \left ( nt\right ) dt=\frac{1}{\pi }\left [ \frac{\sin nt}{n}\right ] _{0}^{\pi }=\frac{1}{n\pi }\sin n\pi =0 \] And\begin{align*} b_{n} & =\frac{1}{\pi }\int _{0}^{\pi }\sin \left ( \frac{2\pi }{T}nt\right ) dt=\frac{1}{\pi }\int _{0}^{\pi }\sin \left ( nt\right ) dt=\frac{1}{\pi }\left [ \frac{-\cos nt}{n}\right ] _{0}^{\pi }=\frac{-1}{n\pi }\left ( \cos n\pi -1\right ) \\ & =\frac{-1}{n\pi }\left ( \left ( -1\right ) ^{n}-1\right ) \\ & =\frac{1+\left ( -1\right ) ^{n+1}}{n\pi } \end{align*}
Therefore\begin{align*} \tilde{f}\left ( t\right ) & =\frac{1}{2}+\sum _{n=1}^{\infty }b_{n}\sin \left ( \frac{2\pi }{T}nt\right ) \\ & =\frac{1}{2}+\sum _{n=1}^{\infty }\frac{1+\left ( -1\right ) ^{n+1}}{n\pi }\sin \left ( nt\right ) \end{align*}

Solution:
The reason to select \(\sin \) series for the spatial solution is to satisfy boundary conditions. We are told the solution at \(t>0\) must be zero at \(x=0\) and at \(x=L\). This is satisfied by \(\sin \left ( \frac{n\pi }{L}x\right ) \). If we had a \(\cos \left ( \frac{n\pi }{L}x\right ) \) term in the spatial solution then that will not vanish at \(x=0\) nor at \(x=L\).
In this problem, we need to find \(b_{n}\left ( t\right ) \), which is the temporal part of the general solution since the spatial solution is provided and it already satisfies the boundary conditions. Hence we just need to determine the form of \(b_{n}\left ( t\right ) \) which will satisfy the two initial conditions given. \(b_{n}\left ( t\right ) \) will contain two constants to be determined from these initial conditions, and this will complete the solution.
To find the general temporal solution, we can start using the standard method of separation of variables. This will lead to second order differential equation to solve for in order to find \(b_{n}\left ( t\right ) \). But with the eigenvalues determined from the spatial solution. This is standard separation of method approach.
Let \[ u\left ( x,t\right ) =T\left ( t\right ) X\left ( x\right ) \] where \(T\left ( t\right ) \) is a function that depends on time only and \(X\left ( x\right ) \) is a function that depends on \(x\) only. We know what \(X\left ( x\right ) \) in this problem. We are given this as \(\sin \left ( \frac{n\pi }{L}x\right ) \). However, we will continue the separation of variables approach in order to find \(T\left ( t\right ) \) and assign this to \(b_{n}\left ( t\right ) \) and in order to find the eigenvalues.
Since we assumed \(u\left ( x,t\right ) =T\left ( t\right ) X\left ( x\right ) \), we will now take derivatives and substitute all these back into the PDE.\begin{align*} \frac{\partial u}{\partial t} & =T^{\prime }X\\ \frac{\partial ^{2}u}{\partial t^{2}} & =T^{\prime \prime }X\\ \frac{\partial u}{\partial x} & =TX^{\prime }\\ \frac{\partial ^{2}u}{\partial x^{2}} & =TX^{\prime \prime } \end{align*}
Therefore the PDE becomes\[ T^{\prime \prime }X=v^{2}TX^{\prime \prime }-kT^{\prime }X \] Dividing by \(TX\)\begin{align*} \frac{T^{\prime \prime }X}{TX} & =v^{2}\frac{TX^{\prime \prime }}{TX}-k\frac{T^{\prime }X}{TX}\\ \frac{T^{\prime \prime }}{T}+k\frac{T^{\prime }}{T} & =v^{2}\frac{X^{\prime \prime }}{X} \end{align*}
We now follow the standard argument of separation of variables and say that the LHS is a function of time only and this is equal to the RHS which is a function of \(x\) only. Therefore, for this to hold, both sides must be equal to some constant, and we choose this constant to be negative, say \(-\omega ^{2}\). (A positive or zero eigenvalues will not lead to real solutions). Therefore, we end up with two differential equations\begin{align*} \frac{T^{\prime \prime }}{T}+k\frac{T^{\prime }}{T} & =-\omega ^{2}\\ v^{2}\frac{X^{\prime \prime }}{X} & =-\omega ^{2} \end{align*}
We always start by the spatial differential equation, which leads to \(X^{\prime \prime }+\frac{\omega ^{2}}{v^{2}}X=0\). Since the stiffness term \(\frac{\omega ^{2}}{v^{2}}\)is positive, then the solution is sinusoidal and stable, hence \[ X=A\cos \left ( \frac{\omega }{v}x\right ) +B\sin \left ( \frac{\omega }{v}x\right ) \] This will lead to the solution given in the problem. But to verify, let us find \(A,B\,\). When \(x=0,\) \(X\left ( 0\right ) =0\), hence \(0=A\). Hence \(X\left ( x\right ) =B\sin \left ( \frac{\omega }{v}x\right ) \). When \(x=L\), \(X\left ( L\right ) =0\), therefore \(0=B\sin \left ( \frac{\omega }{v}L\right ) \). Since we can’t have \(B=0\) else there will be no solution left to use, we force \(\sin \left ( \frac{\omega }{v}L\right ) =0\) which means \(\frac{\omega }{v}L=n\pi \) for integer \(n\) and for any \(B\neq 0\). Therefore, \[ \omega _{n}=v\frac{n\pi }{L}\qquad n=1,2,\cdots \] (We do not need the constant \(B\) any more at this stage, as we can choose \(B=1\) here. The constants will come from the temporal part of the solution). The spatial solution therefore\[ X\left ( x\right ) =\sin \left ( \frac{n\pi }{L}x\right ) \] Which is the solution given.
Now we are ready to find the general solution for \(T\left ( t\right ) \) since we now know the eigenvalues \(\omega _{n}\). We go back to the ODE for \(T\left ( t\right ) \) and solve it. Here it is again\begin{align*} \frac{T^{\prime \prime }}{T}+k\frac{T^{\prime }}{T} & =-\omega _{n}^{2}\\ T^{\prime \prime }+kT^{\prime }+\omega _{n}^{2}T & =0 \end{align*}
This is a standard second order ODE that represents a damped system with stiffness term. The solution depends on the damping. For underdamped system, the solution would look like\[ T_{n}\left ( t\right ) =e^{\frac{-k}{2}t}\left ( A_{n}\cos \left ( \omega _{d}t\right ) +B_{n}\sin \left ( \omega _{d}t\right ) \right ) \] Where \(\omega _{d}\) is the damped natural frequency (this is due to the roots of the characteristic equation being complex conjugates). But here we are told that the damping is large. This must mean it is overdamped, and hence the roots of the characteristic equation are both real and distinct (The solution would have been easier if it is underdamped). Therefore, we can write down the solution as 7
\begin{align*} T_{n}\left ( t\right ) & =A_{n}e^{\lambda _{1}t}+B_{n}e^{\lambda _{2}t}\\ & =A_{n}e^{\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}+B_{n}e^{\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t} \end{align*}
Where \(\omega _{n}=\frac{vn\pi }{L}\). These fundamental solutions can now be added to obtain the general solution\begin{align} u\left ( x,t\right ) & =\sum \limits _{n=1}^{\infty }T_{n}X_{n}\tag{1}\\ & =\sum \limits _{n=1}^{\infty }\left \{ A_{n}e^{\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}+B_{n}e^{\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}\right \} \sin \left ( \frac{n\pi }{L}x\right ) \nonumber \end{align}
We see now that \[ b_{n}\left ( t\right ) =A_{n}e^{\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}+B_{n}e^{\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}\] We are now ready to find \(A_{n},B_{n}\) from initial conditions. When \(t=0\), \(u\left ( x,0\right ) =f\left ( x\right ) \), hence from Eq. (1) we obtain\[ f\left ( x\right ) =\sum \limits _{n=1}^{\infty }\left ( A_{n}+B_{n}\right ) \sin \left ( \frac{n\pi }{L}x\right ) \qquad 0\leq x\leq L \] To find \(A_{n}\) we need to apply the orthogonality relation by multiplying each side by \(\sin \left ( \frac{m\pi }{L}x\right ) \) and integrating and using the fact that \[ \int _{0}^{L}\sin \left ( \frac{n\pi }{L}x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx=\left \{ \begin{array} [c]{ccc}0 & & m\neq n\\ \frac{1}{2}L & & m=n \end{array} \right . \] Therefore\begin{align*} \int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx & =\sum \limits _{n=1}^{\infty }\left ( A_{n}+B_{n}\right ) \int _{0}^{L}\sin \left ( \frac{n\pi }{L}x\right ) \sin \left ( \frac{m\pi }{L}x\right ) \\ \int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx & =\frac{L}{2}\left ( A_{m}+B_{m}\right ) \end{align*}
Hence \begin{equation} A_{n}+B_{n}=\frac{2}{L}\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx\tag{2} \end{equation} Now using the second initial conditions. First, we need to take time derivative of the general solution, which results in\begin{multline*} \frac{\partial u\left ( x,t\right ) }{\partial t}=\\ \sum \limits _{n=1}^{\infty }\left [ A_{n}\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) e^{\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}+B_{n}\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) e^{\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}\right ] \sin \left ( \frac{n\pi }{L}x\right ) \end{multline*} At \(t=0\) the above becomes\[ g\left ( x\right ) =\sum \limits _{n=1}^{\infty }\left [ A_{n}\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) +B_{n}\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) \right ] \sin \left ( \frac{n\pi }{L}x\right ) \] To find \(B_{n}\) we need to apply the orthogonality relation by multiplying each side by \(\sin \left ( \frac{m\pi }{L}x\right ) \) and integrating. Hence\begin{align*} \int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx & =\sum \limits _{n=1}^{\infty }\left [ A_{n}\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) +B_{n}\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) \right ] \\ & \int _{0}^{L}\sin \left ( \frac{n\pi }{L}x\right ) \sin \left ( \frac{m\pi }{L}x\right ) \\ \int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx & =\frac{L}{2}\left [ A_{n}\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) +B_{n}\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) \right ] \end{align*}
Hence\begin{equation} A_{n}\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) +B_{n}\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) =\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx\tag{2} \end{equation} We now have two equations to solve for \(A_{n},B_{n}.\) From Eq (1), \[ A_{n}=-B_{m}+\frac{2}{L}\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx \] Substituting this in Eq. (2) gives\begin{multline*} \left ( -B_{n}+\frac{2}{L}\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx\right ) \left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) \\ +B_{n}\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) =\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx \end{multline*} Solving for \(B_{n}\) gives\begin{multline*} B_{n}\left ( \frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}-\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) \\ +\frac{2}{L}\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) \int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx=\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx \end{multline*} Hence\[ B_{n}=\frac{\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx-\frac{2}{L}\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) \int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx}{2\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}}\] Now that \(B_{n}\) is found, we can find \(A_{n}\) from\[ A_{n}=-B_{n}+\frac{2}{L}\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx \] This complete the solution, all terms are now found. The solution is\[ u\left ( x,t\right ) =\sum _{n=1}^{\infty }b_{n}\left ( t\right ) \sin \left ( \frac{n\pi }{L}x\right ) \] Where\begin{align*} b_{n}\left ( t\right ) & =A_{n}e^{\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}+B_{n}e^{\left ( -\frac{k}{2}+\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) t}\\ A_{n} & =-B_{n}+\frac{2}{L}\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx\\ B_{n} & =\frac{\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx-\frac{2}{L}\left ( -\frac{k}{2}-\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}\right ) \int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx}{2\sqrt{\left ( \frac{k}{2}\right ) ^{2}-\omega _{n}^{2}}}\\ \omega _{n} & =\left ( \frac{vn\pi }{L}\right ) ^{2} \end{align*}
In the above solution, system was assumed to be overdamped. This was done because the problem said the damping is large. It was not clear if this meant overdamped or not. Here is a solution assuming underdamped, which means the solution \(T_{n}\left ( t\right ) \) will have complex roots. Assuming underdamped, the time solution is
\[ T_{n}\left ( t\right ) =e^{\frac{-k}{2}t}\left ( A_{n}\cos \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) +B_{n}\sin \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) \right ) \] Where \(\omega _{n}=\frac{vn\pi }{L}\). These fundamental solutions can now be added to obtain the general solution\begin{align} u\left ( x,t\right ) & =\sum \limits _{n=1}^{\infty }T_{n}X_{n}\tag{1}\\ & =\sum \limits _{n=1}^{\infty }e^{\frac{-k}{2}t}\left ( A_{n}\cos \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) +B_{n}\sin \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) \right ) \sin \left ( \frac{n\pi }{L}x\right ) \nonumber \end{align}
We see now that \[ b_{n}\left ( t\right ) =e^{\frac{-k}{2}t}\left ( A_{n}\cos \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) +B_{n}\sin \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) \right ) \] We are now ready to find \(A_{n},B_{n}\) from initial conditions. When \(t=0\), \(u\left ( x,0\right ) =f\left ( x\right ) \), hence from Eq. (1) we obtain\[ f\left ( x\right ) =\sum \limits _{n=1}^{\infty }A_{n}\sin \left ( \frac{n\pi }{L}x\right ) \qquad 0\leq x\leq L \] To find \(A_{n}\) we need to apply the orthogonality relation by multiplying each side by \(\sin \left ( \frac{m\pi }{L}x\right ) \) and integrating and using the fact that \[ \int _{0}^{L}\sin \left ( \frac{n\pi }{L}x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx=\left \{ \begin{array} [c]{ccc}0 & & m\neq n\\ \frac{1}{2}L & & m=n \end{array} \right . \] Therefore\begin{align*} \int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx & =\sum \limits _{n=1}^{\infty }A_{n}\int _{0}^{L}\sin \left ( \frac{n\pi }{L}x\right ) \sin \left ( \frac{m\pi }{L}x\right ) \\ \int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx & =\frac{L}{2}A_{m} \end{align*}
Hence \[ A_{n}=\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx \] We are not given the form of \(f\left ( x\right ) \) so we determine the exact value of \(A_{n}\). Now we will try to find \(B_{n}\) using the second initial conditions. First, we need to take time derivative of the general solution, which results in\begin{multline*} \frac{\partial u\left ( x,t\right ) }{\partial t}=\sum \limits _{n=1}^{\infty }-\frac{k}{2}e^{\frac{-k}{2}t}\left ( A_{n}\cos \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) +B_{n}\sin \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) \right ) \sin \left ( \frac{n\pi }{L}x\right ) \\ +\sum \limits _{n=1}^{\infty }e^{\frac{-k}{2}t}\left ( -A_{n}\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}\sin \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) +B_{n}\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}\cos \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) \right ) \\ \sin \left ( \frac{n\pi }{L}x\right ) \end{multline*} At \(t=0\) the above becomes\[ g\left ( x\right ) =\sum \limits _{n=1}^{\infty }\left ( -\frac{k}{2}A_{n}+B_{n}\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}\right ) \sin \left ( \frac{n\pi }{L}x\right ) \] To find \(B_{n}\) we need to apply the orthogonality relation by multiplying each side by \(\sin \left ( \frac{m\pi }{L}x\right ) \) and integrating. Hence\begin{align*} \int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx & =\sum \limits _{n=1}^{\infty }\left ( -\frac{k}{2}A_{n}+B_{n}\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}\right ) \int _{0}^{L}\sin \left ( \frac{n\pi }{L}x\right ) \sin \left ( \frac{m\pi }{L}x\right ) \\ \int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{m\pi }{L}x\right ) dx & =\frac{L}{2}\left ( -\frac{k}{2}A_{n}+B_{n}\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}\right ) \\ -\frac{k}{2}A_{n}+B_{n}\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}} & =\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx\\ B_{n}\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}} & =\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx+\frac{k}{2}A_{n}\\ B_{n} & =\frac{\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx+\frac{k}{2}\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx}{\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}} \end{align*}
This complete the solution. The solution is\[ u\left ( x,t\right ) =\sum _{n=1}^{\infty }b_{n}\left ( t\right ) \sin \left ( \frac{n\pi }{L}x\right ) \] Where\begin{align*} b_{n}\left ( t\right ) & =e^{\frac{-k}{2}t}\left ( A_{n}\cos \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) +B_{n}\sin \left ( \sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}t\right ) \right ) \\ A_{n} & =\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx\\ B_{n} & =\frac{\frac{2}{L}\int _{0}^{L}g\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx+\frac{k}{2}\int _{0}^{L}f\left ( x\right ) \sin \left ( \frac{n\pi }{L}x\right ) dx}{\sqrt{\omega _{n}^{2}-\left ( \frac{k}{2}\right ) ^{2}}}\\ \omega _{n} & =\left ( \frac{vn\pi }{L}\right ) ^{2} \end{align*}