Evaluate \(\left ( a\right ) \int _{0}^{1+i}e^{2z}dz\) and \(\left ( b\right ) \int _{C}\frac{z+4}{\left ( z^{2}+1\right ) \left ( z-1\right ) }dz\) where \(C\) is the circle \(\left \vert z\right \vert =2\)
Solution:
part a.
Checking if the function \(f\left ( z\right ) \) is analytic ( This is not actually needed for this part, since integration is not over a closed path).
Let \(z=x+iy\), hence \(f\left ( z\right ) =e^{2z}=e^{2\left ( x+iy\right ) }\,\), hence\begin{align*} f\left ( z\right ) & =e^{2x}\left ( \cos 2y+i\sin 2y\right ) \\ & =e^{2x}\cos 2y+ie^{2x}\sin 2y\\ & =u+iv \end{align*}
Hence \(u=e^{2x}\cos 2y,v=e^{2x}\sin 2y\) and\begin{align*} \frac{\partial u}{\partial x} & =2e^{2x}\cos 2y\\ \frac{\partial v}{\partial y} & =2e^{2x}\cos 2y \end{align*}
Hence \(\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\) and\begin{align*} \frac{\partial u}{\partial y} & =-2e^{2x}\sin 2y\\ \frac{\partial v}{\partial x} & =2e^{2x}\sin 2y \end{align*}
Hence \(\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}\), therefore it is analytic function.
Complex integration can be done along any path. Using the direct path gives\begin{align*} \int _{0}^{1+i}e^{2z}dz & =\left [ \frac{e^{2z}}{2}\right ] _{0}^{1+i}\\ & =\frac{1}{2}\left ( e^{2+2i}-1\right ) \end{align*}
part b:
\[ f\left ( z\right ) =\frac{z+4}{\left ( z^{2}+1\right ) \left ( z-1\right ) }\] This function can be verified to be analytic. Verified using CAS
The function \(f\left ( z\right ) \) is analytic but it does have singularity at \(z=1,-i,+i\), therefore it is not an entire function (An entire function is analytic everywhere and has no singularity).
\(f\left ( z\right ) =\frac{z+4}{\left ( z-i\right ) (z+i)\left ( z-1\right ) }\) has all its poles inside \(C\), therefore, using residual theory \(\int _{C}f\left ( z\right ) dz=2\pi i\sum \limits _{k}residual\left ( f\left ( z\right ) \right ) _{k}\) gives \begin{align*} \int _{C}f\left ( z\right ) dz & =2\pi i\left [ \left ( \frac{z+4}{\left ( z-i\right ) (z+i)}\right ) _{z=1}+\left ( \frac{z+4}{\left ( z-i\right ) \left ( z-1\right ) }\right ) _{z=-i}+\left ( \frac{z+4}{(z+i)\left ( z-1\right ) }\right ) _{z=i}\right ] \\ & =2\pi i\left ( \frac{1+4}{\left ( 1-i\right ) (1+i)}+\frac{-i+4}{\left ( -i-i\right ) \left ( -i-1\right ) }+\frac{i+4}{(i+i)\left ( i-1\right ) }\right ) \\ & =2\pi i\left ( \frac{5}{2}+\frac{-i+4}{-2+2i}+\frac{i+4}{-2-2i}\right ) \\ & =2\pi i\left ( \frac{5}{2}+\frac{-i+4}{-2+2i}+\frac{i+4}{-2-2i}\right ) \\ & =2\pi i\left ( \frac{5}{2}-\frac{5}{2}\right ) \\ & =0 \end{align*}
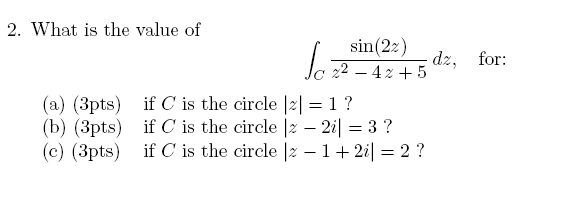
Solution
The integrand \(f\left ( z\right ) \) is \(\frac{\sin \left ( 2z\right ) }{\left ( z-(2-i)\right ) \left ( z-(2+i)\right ) }\), hence it is poles at \(z_{1}=2-i\) and \(z_{2}=2+i\)
part a
In this case, both poles are outside \(C\), which is unit circle centered at \(0\), hence \(\int _{C}\frac{\sin \left ( 2z\right ) }{\left ( z-(2-i)\right ) \left ( z-(2+i)\right ) }dz=0\)
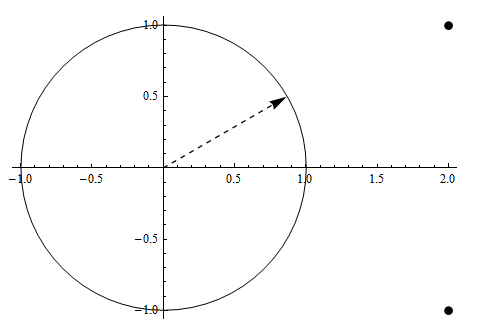
part b
In this case, the circle is centered at \(2i\) and its radius is \(3\). A plot shows the location so of poles
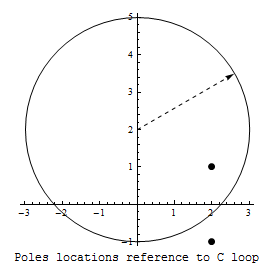
We see there is one pole inside \(C\) from the plot. But to determine if each pole is inside \(C\) or not, we check for \(\left \vert z_{i}-center\right \vert \) and see if this is less than the circle radius or not. We do this for each pole. For pole \(z_{1}=2-i\) we obtain \(\left \vert \left ( 2-i\right ) -\left ( 2i\right ) \right \vert =\left \vert 2+3i\right \vert =\sqrt{4+9}=\sqrt{13}=3.605\) hence this pole is outside \(C\) as shown in the diagram. For pole \(z_{2}=2+i\) we obtain \(\left \vert \left ( 2+i\right ) -\left ( 2i\right ) \right \vert =\left \vert 2-i\right \vert =\sqrt{4+1}=\sqrt{5}=2.236\) which is smaller that the radius of the circle \(C\) hence this pole is inside. Therefore, using the residual theorem we obtain\begin{align*} \int _{C}f\left ( z\right ) dz & =2\pi i\left [ \left ( \frac{\sin \left ( 2z\right ) }{\left ( z-(2-i)\right ) }\right ) _{z=\left ( 2+i\right ) }\right ] \\ & =2\pi i\left ( \frac{\sin \left ( 2\left ( 2+i\right ) \right ) }{\left ( \left ( 2+i\right ) -(2-i)\right ) }\right ) \\ & =2\pi i\frac{\sin \left ( 4+2i\right ) }{2i}\\ & =\pi \sin \left ( 4+2i\right ) \end{align*}
Part c
In this case, the circle is \(\left \vert z-\left ( 1-2i\right ) \right \vert =2\,\,\), hence it is centered at point \(\left ( 1,-2i\right ) \) and its radius is \(2.\)
For pole \(z_{1}=2-i\) we obtain \(\left \vert \left ( 2-i\right ) -\left ( 1-2i\right ) \right \vert =\left \vert 1+i\right \vert =\sqrt{2}\) hence this pole is inside \(C\) as shown in the diagram below. For pole \(z_{2}=2+i\) we obtain \(\left \vert \left ( 2+i\right ) -\left ( 1-2i\right ) \right \vert =\left \vert 1+3i\right \vert =\sqrt{1+9}=\sqrt{10}=\allowbreak 3.162\,3\) which is larger than the radius of the circle \(C\) hence this pole is outside.
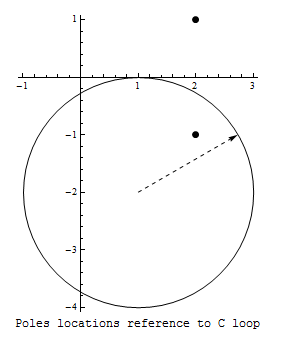
Therefore, using the residual theorem \begin{align*} \int _{C}f\left ( z\right ) dz & =2\pi i\left [ \left ( \frac{\sin \left ( 2z\right ) }{\left ( z-(2+i)\right ) }\right ) _{z=\left ( 2-i\right ) }\right ] \\ & =2\pi i\left ( \frac{\sin \left ( 2\left ( 2-i\right ) \right ) }{\left ( \left ( 2-i\right ) -(2+i)\right ) }\right ) \\ & =2\pi i\frac{\sin \left ( 4-2i\right ) }{-2i}\\ & =-\pi \sin \left ( 4+2i\right ) \end{align*}

Solution
Part (a)
The poles of \(f\left ( z\right ) =\frac{2z^{3}}{\left ( z-2\right ) ^{2}}\) are at \(z=2\) (order 2). The following plot shows the location of the pole relative to \(\Gamma \)

The pole is inside \(\Gamma \,\ \)hence using residual we obtain\[ \int _{C}f\left ( z\right ) dz=2\pi i\left [ \frac{1}{\left ( n-1\right ) !}\left ( \frac{d^{n-1}}{dz^{n-1}}2z^{3}\right ) _{z=2}\right ] \] Where \(n=2\) in the above, since that is the order of the pole. Therefore\begin{align*} \int _{C}f\left ( z\right ) dz & =2\pi i\left [ \left ( \frac{d}{dz}2z^{3}\right ) _{z=2}\right ] \\ & =\left ( 2\pi i\right ) \left ( 6z^{2}\right ) _{z=2}\\ & =\left ( 2\pi i\right ) \left ( 6\left ( 2\right ) ^{2}\right ) \\ & =48\pi i \end{align*}
Part b
The poles of \(f\left ( z\right ) =\frac{\cos \left ( z-i\right ) }{\left ( z+2i\right ) ^{3}}\). The poles are at \(z=-2i\) of order \(3\). Therefore \(\Gamma \) includes the pole inside it, and we can use the residual, hence\[ \int _{C}f\left ( z\right ) dz=2\pi i\left [ \frac{1}{\left ( n-1\right ) !}\left ( \frac{d^{n-1}}{dz^{n-1}}\cos \left ( z-i\right ) \right ) _{z=-2i}\right ] \] Where \(n=3\) in the above, since that is the order of the pole. Therefore\begin{align*} \int _{C}f\left ( z\right ) dz & =2\pi i\left [ \frac{1}{2}\left ( \frac{d^{2}}{dz^{2}}\cos \left ( z-i\right ) \right ) _{z=-2i}\right ] \\ & =2\pi i\left [ \frac{1}{2}\left ( \frac{d}{dz}\left ( -\sin \left ( z-i\right ) \right ) \right ) _{z=-2i}\right ] \\ & =2\pi i\left [ \frac{1}{2}\left ( -\cos \left ( z-i\right ) \right ) _{z=-2i}\right ] \\ & =2\pi i\frac{1}{2}\left ( -\cos \left ( -2i-i\right ) \right ) \\ & =-\pi i\cos \left ( -3i\right ) \end{align*}
Or\[ \int _{C}f\left ( z\right ) dz=-i\pi \cosh \left ( 3\right ) \]
Part c
\(f\left ( z\right ) =\left ( z-i\right ) ^{2}\) has no poles. Hence if we can show it is analytic, then the closed path integral will be zero by Cauchy theorem. We can verify also it is analytic. Let \(z=x+iy\), hence \begin{align*} f\left ( z\right ) & =\left ( \left ( x+iy\right ) -i\right ) ^{2}\\ & =x^{2}+2ixy-2ix-y^{2}+2y-1\\ & =\left ( x^{2}-y^{2}-1\right ) +i\left ( 2xy-2x\right ) \end{align*}
\(\,\)Therefore \(u=x^{2}-y^{2}-1\) and \(v=2xy-2x\) and\begin{align*} \frac{\partial u}{\partial x} & =2x\\ \frac{\partial v}{\partial y} & =2x \end{align*}
Hence \(\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\) and\begin{align*} \frac{\partial u}{\partial y} & =-2y\\ \frac{\partial v}{\partial x} & =2y-2 \end{align*}
Hence \(\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}\), therefore it is analytic function and the integral is zero.
Expand \(f\left ( z\right ) =\frac{1}{z^{2}+3z+2}\) in Taylor series. (a) About point \(z=0\) (b) about point \(z=2\). Determine the radius of convergence for each case.
Solution:
Taylor series is defined as\[ f\left ( z\right ) =f\left ( a\right ) +\left ( z-a\right ) f^{\prime }\left ( a\right ) +\frac{\left ( z-a\right ) ^{2}}{2!}f^{\prime \prime }\left ( a\right ) +\cdots +\frac{\left ( z-a\right ) ^{n-1}}{\left ( n-1\right ) !}f^{\left ( n-1\right ) }\left ( a\right ) +R_{n}\] However, we do not calculate the series directly from the above definition. Instead, using power series method, we can formulate this to finding the series\[ f\left ( z\right ) =\sum \limits _{n=0}^{\infty }c_{n}\left ( z-z_{0}\right ) ^{n}\] Where \(z_{0}\) is the point to expand around. In this case it is zero. We need to find \(c_{n}.\)
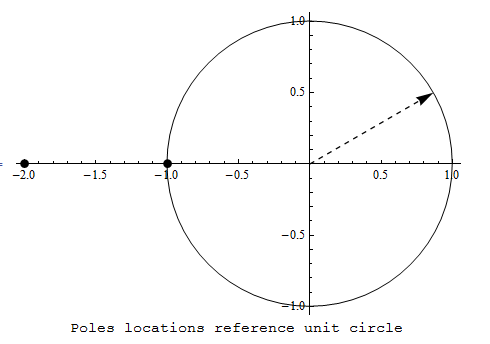
To find radius of convergence \(\rho \), we draw a circle, centered at the point of expansion, and extend it all the way to the first pole. \(f\left ( z\right ) =\frac{1}{\left ( z+2\right ) \left ( z+1\right ) }\) hence it has a pole at \(z=-2\) and \(z=-1\,.\)therefore, \[ \rho =1 \] Here is a diagram
Where the first geometric series converges for \(\left \vert z\right \vert <1\) and the second converges for \(\left \vert \frac{z}{2}\right \vert <1\) or \(\left \vert z\right \vert <2\). The series is\begin{align*} f\left ( z\right ) & =\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}z^{n}-\frac{1}{2}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{z}{2}\right ) ^{n}\\ & =\left ( 1-z+z^{2}-z^{3}+z^{4}+\cdots \right ) -\frac{1}{2}\left ( 1-\frac{z}{2}+\frac{z^{2}}{2^{2}}-\frac{z^{3}}{2^{3}}+\frac{z^{4}}{2^{4}}+\cdots \right ) \\ & =\left ( 1-z+z^{2}-z^{3}+z^{4}+\cdots \right ) +\left ( -\frac{1}{2}+\frac{z}{2^{2}}-\frac{z^{2}}{2^{3}}+\frac{z^{3}}{2^{4}}-\frac{z^{4}}{2^{5}}+\cdots \right ) \\ & =\frac{1}{2}-z\left ( 1-\frac{1}{2^{2}}\right ) +z^{2}\left ( 1-\frac{1}{2^{3}}\right ) -z^{3}\left ( 1-\frac{1}{2^{4}}\right ) +\cdots \\ & =\frac{1}{2}-\frac{3}{4}z+\frac{7}{8}z^{3}-\frac{15}{16}z^{3}+\cdots \end{align*}
\[ f\left ( z\right ) =\sum \limits _{n=0}^{\infty }c_{n}\left ( z-z_{0}\right ) ^{n}\] Where \(z_{0}\) is the point to expand around. In this case it is 2.
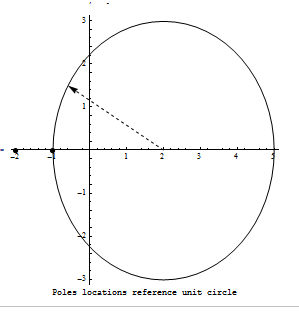
To find radius of convergence \(\rho \), we make a circle, centered at the point of expansion, and extend it all the way to the first pole. Therefore radius of convergence is \[ \rho =3 \] As shown in this diagram
We need to find \(c_{n}.\) Writing \begin{align*} f\left ( z\right ) & =\frac{1}{z^{2}+3z+2}=\frac{1}{\left ( z+2\right ) \left ( z+1\right ) }\\ & =\frac{1}{z+1}-\frac{1}{z+2}\\ & =\frac{1}{\left ( z-2\right ) +3}-\frac{1}{\left ( z-2\right ) +4}\\ & =\frac{1}{3}\frac{1}{1+\left ( \frac{z-2}{3}\right ) }-\frac{1}{4}\frac{1}{1+\left ( \frac{z-2}{4}\right ) }\\ & =\frac{1}{3}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{z-2}{3}\right ) ^{n}-\frac{1}{4}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{z-2}{4}\right ) ^{n} \end{align*}
Where the first geometric series converges for \(\left \vert \frac{z-2}{3}\right \vert <1\) or \(\left \vert z-2\right \vert <3\) or \(\left \vert z\right \vert <5\) and the second converges for \(\left \vert \frac{z-2}{4}\right \vert <1\) or \(\left \vert z-2\right \vert <4\) or \(\left \vert z\right \vert <6\). And the series is\begin{align*} f\left ( z\right ) & =\frac{1}{3}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{z-2}{3}\right ) ^{n}-\frac{1}{4}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{z-2}{4}\right ) ^{n}\\ & \\ & =\frac{1}{3}\left ( 1-\frac{1}{3}\left ( z-2\right ) +\left ( \frac{1}{3}\right ) ^{2}\left ( z-2\right ) ^{2}-\left ( \frac{1}{3}\right ) ^{2}\left ( z-2\right ) ^{3}+\cdots \right ) \\ & -\frac{1}{4}\left ( 1-\frac{1}{4}\left ( z-2\right ) +\left ( \frac{1}{4}\right ) ^{2}\left ( z-2\right ) ^{2}-\left ( \frac{1}{4}\right ) ^{3}\left ( z-2\right ) ^{3}+\cdots \right ) \\ & \\ & =\left ( \frac{1}{3}-\frac{1}{9}\left ( z-2\right ) +\frac{1}{27}\left ( z-2\right ) ^{2}-\frac{1}{27}\left ( z-2\right ) ^{3}+\cdots \right ) \\ & -\left ( \allowbreak \frac{1}{4}-\frac{1}{16}\left ( z-2\right ) +\frac{1}{64}\left ( z-2\right ) ^{2}-\frac{1}{256}\left ( z-2\right ) ^{3}+\cdots \right ) \\ & \\ & =\frac{1}{12}-\frac{7}{144}\left ( z-2\right ) +\frac{37}{1728}\left ( z-2\right ) ^{2}-\frac{229}{6912}\left ( z-2\right ) ^{3}+\cdots \end{align*}

solution
part (a)
\[ f\left ( z\right ) =\frac{1}{2+z}\] around point \(1-8i\).
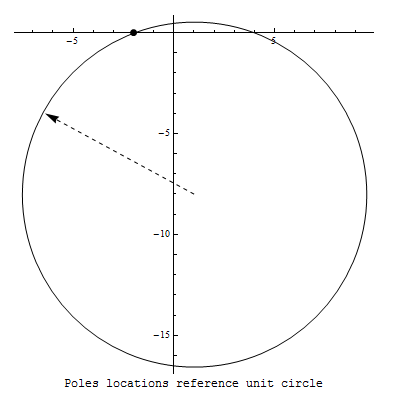
To find radius of convergence \(\rho \), we make a circle, centered at the point of expansion, and extend it all the way to the first pole. \(f\left ( z\right ) =\frac{1}{2+z}\) hence it has a pole at \(z=-2,\) Therefore, \[ \rho =\sqrt{3^{2}+8^{2}}=\sqrt{73}\]
As seen by this diagram.
Now the Taylor series is found
\[ f\left ( z\right ) =\sum \limits _{n=0}^{\infty }c_{n}\left ( z-z_{0}\right ) ^{n}\] Where \(z_{0}\) is the point to expand around. In this case it is \(1-8i\). We need to find \(c_{n}.\) Writing \begin{align*} f\left ( z\right ) & =\frac{1}{2+z}=\frac{1}{2+z-\left ( 1-8i\right ) +\left ( 1-8i\right ) }\\ & =\frac{1}{\left ( 3-8i\right ) +\left ( z-\left ( 1-8i\right ) \right ) }\\ & =\frac{1}{\left ( 3-8i\right ) }\frac{1}{1+\frac{1}{3-8i}\left ( z-\left ( 1-8i\right ) \right ) }\\ & =\frac{1}{\left ( 3-8i\right ) }\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{1}{3-8i}\right ) ^{n}\left ( z-\left ( 1-8i\right ) \right ) ^{n} \end{align*}
Hence\begin{align*} f\left ( z\right ) & =\frac{1}{\left ( 3-8i\right ) }\left ( 1-\left ( \frac{1}{3-8i}\right ) \left ( z-\left ( 1-8i\right ) \right ) +\left ( \frac{1}{3-8i}\right ) ^{2}\left ( z-\left ( 1-8i\right ) \right ) ^{2}+\cdots \right ) \\ & =\frac{1}{\left ( 3-8i\right ) }-\frac{1}{\left ( 3-8i\right ) ^{2}}\left ( z-\left ( 1-8i\right ) \right ) +\frac{1}{\left ( 3-8i\right ) ^{3}}\left ( z-\left ( 1-8i\right ) \right ) ^{2}+\cdots \\ & =\left ( \frac{3}{73}+\frac{8i}{73}\right ) +\left ( \frac{55}{5329}-\frac{48i}{5329}\right ) \left ( z-\left ( 1-8i\right ) \right ) -\left ( \frac{549}{389017}+\frac{296i}{389017}\right ) \left ( z-\left ( 1-8i\right ) \right ) ^{2}+\cdots \end{align*}
part (b)
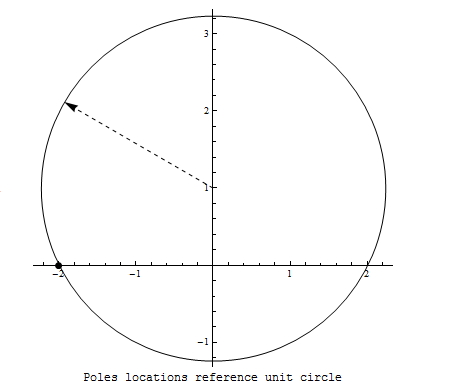
\(f\left ( z\right ) =1+\frac{1}{2+z^{2}}\) around point \(i\). In this case, the center of circle is at \(i\) and hence\[ \rho =\sqrt{1^{2}+2^{2}}=\sqrt{5}\] As shown in this diagram
And Taylor series is \begin{align*} f\left ( z\right ) & =1+\frac{1}{2+z^{2}}\\ & =1+\frac{1}{\left ( z-i\sqrt{2}\right ) \left ( z+i\sqrt{2}\right ) } \end{align*}
Doing partial fractions gives\[ f\left ( z\right ) =1+\frac{1}{2\sqrt{2}}\frac{1}{\sqrt{2}-iz}+\frac{1}{2\sqrt{2}}\frac{1}{\sqrt{2}+iz}\] Convert so that \(z-i\) appears. \(iz=i\left ( z-i\right ) -1\), hence\begin{align} f\left ( z\right ) & =1+\frac{1}{2\sqrt{2}}\frac{1}{\sqrt{2}-\left ( i\left ( z-i\right ) -1\right ) }+\frac{1}{2\sqrt{2}}\frac{1}{\sqrt{2}+\left ( i\left ( z-i\right ) -1\right ) }\nonumber \\ & =1+\frac{1}{2\sqrt{2}}\frac{1}{\sqrt{2}-i\left ( z-i\right ) +1}+\frac{1}{2\sqrt{2}}\frac{1}{\sqrt{2}+i\left ( z-i\right ) -1}\nonumber \\ & =1+\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}+1\right ) -i\left ( z-i\right ) }+\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}-1\right ) +i\left ( z-i\right ) }\nonumber \\ & =1+\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}+1\right ) }\frac{1}{1-\frac{i}{\left ( \sqrt{2}+1\right ) }\left ( z-i\right ) }+\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}-1\right ) }\frac{1}{1+\frac{i}{\left ( \sqrt{2}-1\right ) }\left ( z-i\right ) }\tag{1} \end{align}
Now geometric series can be used.\begin{align*} \frac{1}{1-\frac{i}{\left ( \sqrt{2}+1\right ) }\left ( z-i\right ) } & =\sum _{n}^{\infty }\left ( \frac{i}{\left ( \sqrt{2}+1\right ) }\right ) ^{n}\left ( z-i\right ) ^{n}\\ & =1+\frac{i}{\sqrt{2}+1}\left ( z-i\right ) -\frac{1}{\left ( \sqrt{2}+1\right ) ^{2}}\left ( z-i\right ) ^{2}-\frac{i}{\left ( \sqrt{2}+1\right ) ^{3}}\left ( z-i\right ) ^{3}+\frac{1}{\left ( \sqrt{2}+1\right ) ^{4}}\left ( z-i\right ) ^{4}\cdots \end{align*}
And\begin{align*} \frac{1}{1+\frac{i}{\left ( \sqrt{2}-1\right ) }\left ( z-i\right ) } & =\sum _{n}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{i}{\left ( \sqrt{2}-1\right ) }\right ) ^{n}\left ( z-i\right ) ^{n}\\ & =1-\frac{i}{\sqrt{2}-1}\left ( z-i\right ) +\frac{1}{\left ( \sqrt{2}-1\right ) ^{2}}\left ( z-i\right ) ^{2}-\frac{i}{\left ( \sqrt{2}-1\right ) ^{3}}\left ( z-i\right ) ^{3}+\frac{1}{\left ( \sqrt{2}-1\right ) ^{4}}\left ( z-i\right ) ^{4}\cdots \end{align*}
Substituing the above into Eq. (1) gives\begin{align*} f\left ( z\right ) & =1+\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}+1\right ) }\left ( 1+\frac{i}{\sqrt{2}+1}\left ( z-i\right ) -\frac{1}{\left ( \sqrt{2}+1\right ) ^{2}}\left ( z-i\right ) ^{2}-\frac{i}{\left ( \sqrt{2}+1\right ) ^{3}}\left ( z-i\right ) ^{3}+\frac{1}{\left ( \sqrt{2}+1\right ) ^{4}}\left ( z-i\right ) ^{4}\cdots \right ) \\ & +\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}-1\right ) }\left ( 1-\frac{i}{\sqrt{2}-1}\left ( z-i\right ) +\frac{1}{\left ( \sqrt{2}-1\right ) ^{2}}\left ( z-i\right ) ^{2}+\frac{i}{\left ( \sqrt{2}-1\right ) ^{3}}\left ( z-i\right ) ^{3}-\frac{1}{\left ( \sqrt{2}-1\right ) ^{4}}\left ( z-i\right ) ^{4}\cdots \right ) \end{align*}
Looking at coefficient of term \(\left ( z-i\right ) ^{n}\) power. For \(n=0\) power the term is \begin{align*} c_{0} & =1+\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}+1\right ) }+\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}-1\right ) }\\ & =2 \end{align*}
And for \(c_{1}\) it is\begin{align*} c_{1} & =\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}+1\right ) }\frac{i}{\sqrt{2}+1}-\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}-1\right ) }\frac{i}{\sqrt{2}-1}\\ & =-2i \end{align*}
And for \(c_{2}\)\begin{align*} c_{2} & =-\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}+1\right ) }\frac{1}{\left ( \sqrt{2}+1\right ) ^{2}}-\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}-1\right ) }\frac{1}{\left ( \sqrt{2}-1\right ) ^{2}}\\ & =-5 \end{align*}
And for \(c_{3}\)\begin{align*} c_{2} & =-\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}+1\right ) }\frac{i}{\left ( \sqrt{2}+1\right ) ^{3}}+\frac{1}{2\sqrt{2}}\frac{1}{\left ( \sqrt{2}-1\right ) }\frac{i}{\left ( \sqrt{2}-1\right ) ^{3}}\\ & =12i \end{align*}
and so on. Hence the series is\begin{align*} f\left ( z\right ) & =c_{0}+c_{1}\left ( z-i\right ) +c_{2}\left ( z-i\right ) ^{2}+c_{3}\left ( z-i\right ) ^{3}+\cdots \\ & =2-2i\left ( z-i\right ) -5\left ( z-i\right ) ^{2}+12i\left ( z-i\right ) ^{3}+\cdots \end{align*}