Obtain two distinct Laurent expansions for f\left ( z\right ) =\frac{3z+1}{z^{2}-1} around z=1 and tell where each converges.
Solution
f\left ( z\right ) has singularities at z=\pm 1 and the expansion is around one of these singularities. Looking at the diagram
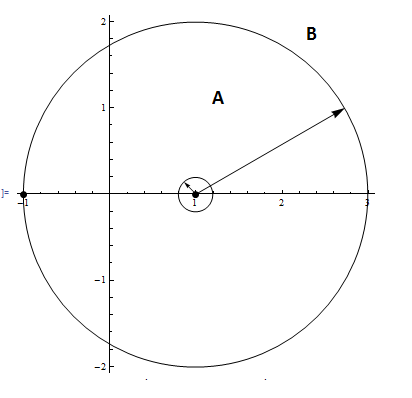
Region A is annulus between z=1 and z=-1 but does not include z=1 where the small circle is shown since that is a singularity. Region B is all the region outside the large circle shown. f\left ( z\right ) =\frac{3z+1}{\left ( z-1\right ) \left ( z+1\right ) }=\frac{2}{z-1}+\frac{1}{z+1} Region A
For \frac{2}{z-1}, since its pole is at z=1 and so we expand outwards, and hence it is already in form of Laurent series around z=1, and for \frac{1}{z+1} since its pole is at z=-1, hence we expand inwards, and so it is expanded in Taylor series f\left ( z\right ) =\overset{Laurent}{\overbrace{\frac{2}{z-1}}}+\overset{Taylor}{\overbrace{\frac{1}{z+1}}} Looking at the second term above, expand in Taylor series\begin{align*} \frac{1}{z+1} & =\frac{1}{\left ( z-1\right ) +1+1}=\frac{1}{\left ( z-1\right ) +2}=\frac{1}{2}\frac{1}{1+\frac{1}{2}\left ( z-1\right ) }\\ & =\frac{1}{2}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{1}{2}\right ) ^{n}\left ( z-1\right ) ^{n}\qquad \left \vert z-1\right \vert <2 \end{align*}
Therefore, for region A\begin{align*} f\left ( z\right ) & =\frac{2}{z-1}+\frac{1}{2}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{1}{2}\right ) ^{n}\left ( z-1\right ) ^{n}\\ & =\frac{2}{z-1}+\frac{1}{2}\left ( 1-\frac{1}{2}\left ( z-1\right ) +\frac{1}{4}\left ( z-1\right ) ^{2}-\frac{1}{16}\left ( z-1\right ) ^{3}+\cdots \right ) \\ & =\frac{2}{z-1}+\frac{1}{2}-\frac{1}{4}\left ( z-1\right ) +\frac{1}{8}\left ( z-1\right ) ^{2}-\frac{1}{16}\left ( z-1\right ) ^{3}+\cdots \end{align*}
This is valid for 0<\left \vert z-1\right \vert <2,z\neq 1
Region B
This is the region outside the large circle to infinity. Since expanding outwards, both terms will use Laurent series now. f\left ( z\right ) =\overset{Laurent}{\overbrace{\frac{2}{z-1}}}+\overset{Laurent}{\overbrace{\frac{1}{z+1}}} \frac{2}{z-1} is already in Laurent series, for the second term\begin{align*} \frac{1}{z+1} & =\frac{1}{\left ( z-1\right ) +1+1}=\frac{1}{\left ( z-1\right ) +2}=\frac{1}{\left ( z-1\right ) }\frac{1}{1+\frac{2}{z-1}}\\ & =\frac{1}{\left ( z-1\right ) }\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\frac{2^{n}}{\left ( z-1\right ) ^{n}}\qquad \left \vert z-1\right \vert >2 \end{align*}
Hence\begin{align*} f\left ( z\right ) & =\frac{2}{z-1}+\frac{1}{\left ( z-1\right ) }\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\frac{2^{n}}{\left ( z-1\right ) ^{n}}\\ & =\frac{2}{z-1}+\frac{1}{\left ( z-1\right ) }\left ( 1-\frac{2}{\left ( z-1\right ) }+\frac{4}{\left ( z-1\right ) ^{2}}-\frac{8}{\left ( z-1\right ) ^{3}}+\cdots \right ) \\ & =\frac{2}{z-1}+\frac{1}{z-1}-\frac{2}{\left ( z-1\right ) ^{2}}+\frac{4}{\left ( z-1\right ) ^{3}}-\frac{8}{\left ( z-1\right ) ^{4}}+\cdots \\ & =\frac{3}{z-1}-\frac{2}{\left ( z-1\right ) ^{2}}+\frac{4}{\left ( z-1\right ) ^{3}}-\frac{8}{\left ( z-1\right ) ^{4}}+\cdots \end{align*}
This is valid for \left \vert z-1\right \vert >2
f\left ( z\right ) =\frac{z+1}{z^{2}\left ( z+2\right ) }, Poles are z=0 order 2 and z=-2 order 1. The pole z=-2 is outside C hence it will not have an effect. To find the residue due to pole z=0\begin{align*} residue\left ( z=0\right ) & =\frac{1}{\left ( 2-1\right ) !}\lim _{z\rightarrow 0}\frac{d}{dz}\left ( z^{2}f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow 0}\frac{d}{dz}\left ( z^{2}\frac{z+1}{z^{2}\left ( z+2\right ) }\right ) \\ & =\lim _{z\rightarrow 0}\frac{d}{dz}\left ( \frac{z+1}{z+2}\right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{1}{z+2}-\frac{\left ( z+1\right ) }{\left ( z+2\right ) ^{2}}\right ) \\ & =\frac{1}{2}-\frac{1}{4}\\ & =\frac{1}{4} \end{align*}
Hence \begin{align*} \oint f\left ( z\right ) dz & =2\pi i\left ( \frac{1}{4}\right ) \\ & =\frac{1}{2}\pi i \end{align*}
f\left ( z\right ) =\frac{z^{2}}{\left ( z^{2}+3z+2\right ) ^{2}} the poles are the roots of \left ( z^{2}+3z+2\right ) ^{2}=0 which is \left ( \left ( z+2\right ) \left ( z+1\right ) \right ) ^{2}=0 or \left ( z+2\right ) ^{2}\left ( z+1\right ) ^{2}=0, hence poles at \left ( z+2\right ) ^{2}=0 or z=-2 and \left ( z+1\right ) ^{2}=0 or z=-1 Only pole at z=-1 is inside C. This is order 2 since the denominator is order 2. Hence\begin{align*} residue\left ( z=-1\right ) & =\frac{1}{\left ( 2-1\right ) !}\lim _{z\rightarrow -1}\frac{d}{dz}\left ( \left ( z+1\right ) ^{2}f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow -1}\frac{d}{dz}\left ( \left ( z+1\right ) ^{2}\frac{z^{2}}{\left ( z+2\right ) ^{2}\left ( z+1\right ) ^{2}}\right ) \\ & =\lim _{z\rightarrow -1}\frac{d}{dz}\left ( \frac{z^{2}}{\left ( z+1\right ) ^{2}}\right ) \\ & =\lim _{z\rightarrow -1}\left ( \frac{2z}{\left ( z+2\right ) ^{2}}-2z^{2}\left ( z+2\right ) ^{-3}\right ) \\ & =\lim _{z\rightarrow -1}\left ( \frac{2z}{\left ( z+2\right ) ^{2}}-\frac{2z^{2}}{\left ( z+2\right ) ^{3}}\right ) \\ & =\left ( \frac{-2}{\left ( -1+2\right ) ^{2}}-\frac{2\left ( -1\right ) ^{2}}{\left ( -1+2\right ) ^{3}}\right ) \\ & =\left ( -2-2\right ) \\ & =-4 \end{align*}
Hence\begin{align*} \oint f\left ( z\right ) dz & =2\pi i\left ( -4\right ) \\ & =-8\pi i \end{align*}
f\left ( z\right ) =\frac{1}{z\left ( z^{2}+6z+4\right ) }=\frac{1}{z\left ( z-\left ( \sqrt{5}-3\right ) \right ) \left ( z-\left ( -\sqrt{5}-3\right ) \right ) }=\frac{1}{z\left ( z-\left ( \sqrt{5}-3\right ) \right ) \left ( z-\left ( -\sqrt{5}-3\right ) \right ) }. Since \sqrt{5}-3=-5.\,\allowbreak 236\,1 and -\sqrt{5}-3=-0.763\,93 then only z=\left ( -\sqrt{5}-3\right ) is inside C.
Hence poles are z=0 and z=\left ( -\sqrt{5}-3\right ) and both is order 1.\begin{align*} residue\left ( z=0\right ) & =\lim _{z\rightarrow 0}\left ( zf\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow 0}\left ( z\frac{1}{z\left ( z^{2}+6z+4\right ) }\right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{1}{\left ( z^{2}+6z+4\right ) }\right ) \\ & =\frac{1}{4} \end{align*}
And\begin{align*} residue\left ( z=\left ( -\sqrt{5}-3\right ) \right ) & =\lim _{z\rightarrow \left ( -\sqrt{5}-3\right ) }\left ( \left ( z-\left ( -\sqrt{5}-3\right ) \right ) f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow \left ( -\sqrt{5}-3\right ) }\left ( \left ( z-\left ( -\sqrt{5}-3\right ) \right ) \frac{1}{z\left ( z-\left ( \sqrt{5}-3\right ) \right ) \left ( z-\left ( -\sqrt{5}-3\right ) \right ) }\right ) \\ & =\lim _{z\rightarrow \left ( -\sqrt{5}-3\right ) }\left ( \frac{1}{z\left ( z-\left ( \sqrt{5}-3\right ) \right ) }\right ) \\ & =\frac{1}{\left ( -\sqrt{5}-3\right ) \left ( \left ( -\sqrt{5}-3\right ) -\left ( \sqrt{5}-3\right ) \right ) }\\ & =\frac{1}{\left ( -\sqrt{5}-3\right ) \left ( -\sqrt{5}-3-\sqrt{5}+3\right ) }\\ & =\frac{1}{\left ( -\sqrt{5}-3\right ) \left ( -2\sqrt{5}\right ) }\\ & =\frac{1}{10+6\sqrt{5}} \end{align*}
Hence\begin{align*} \oint f\left ( z\right ) dz & =2\pi i\left ( \frac{1}{4}+\frac{1}{10+6\sqrt{5}}\right ) \\ & =\left ( \frac{1}{2}+\frac{1}{5+3\sqrt{5}}\right ) \pi i\\ & =0.5854\pi i \end{align*}
Show that f\left ( z\right ) =\frac{\cosh \left ( z\right ) -1}{\sinh \left ( z\right ) -z} has simple pole at z=0 and find its residue there.
Solution
Expanding \cosh \left ( z\right ) and \sinh \left ( z\right ) in series gives f\left ( z\right ) =\frac{\left ( 1+\frac{z^{2}}{2!}+\frac{z^{4}}{4!}+\frac{z^{6}}{6!}\right ) -1}{\left ( z+\frac{z^{3}}{3!}+\frac{z^{5}}{5!}+\frac{z^{7}}{7!}\right ) -z}=\frac{\frac{z^{2}}{2!}+\frac{z^{4}}{4!}+\frac{z^{6}}{6!}}{\frac{z^{3}}{3!}+\frac{z^{5}}{5!}+\frac{z^{7}}{7!}} Divide by z^{2}\begin{align*} f\left ( z\right ) & =\frac{\frac{1}{2!}+\frac{z^{2}}{4!}+\frac{z^{4}}{6!}}{\frac{z}{3!}+\frac{z^{3}}{5!}+\frac{z^{5}}{7!}}\\ & =\frac{\frac{1}{2!}+\frac{z^{2}}{4!}+\frac{z^{4}}{6!}}{z\left ( \frac{1}{3!}+\frac{z^{2}}{5!}+\frac{z^{4}}{7!}\right ) } \end{align*}
Therefore, f\left ( z\right ) has simple pole at z=0. The residue is\begin{align*} residue\left ( z=0\right ) & =\lim _{z\rightarrow 0}\left ( zf\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow 0}\left ( z\frac{\cosh \left ( z\right ) -1}{\sinh \left ( z\right ) -z}\right ) \\ & =\lim _{z\rightarrow 0}\left ( z\frac{\frac{1}{2!}+\frac{z^{2}}{4!}+\frac{z^{4}}{6!}}{z\left ( \frac{1}{3!}+\frac{z^{2}}{5!}+\frac{z^{4}}{7!}\right ) }\right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{\frac{1}{2!}+\frac{z^{2}}{4!}+\frac{z^{4}}{6!}}{\left ( \frac{1}{3!}+\frac{z^{2}}{5!}+\frac{z^{4}}{7!}\right ) }\right ) \\ & =\frac{\frac{1}{2!}}{\frac{1}{3!}}\\ & =\frac{6}{2}\\ & =3 \end{align*}
Evaluate the following using the method of residues (a) \int _{0}^{\pi }\frac{\cos \left ( 2\theta \right ) }{5+4\cos \theta }d\theta (b)\int _{0}^{2\pi }\frac{\sin ^{2}\theta }{a+b\cos \theta }d\theta where 0<b<a and (c) \int _{-\infty }^{\infty }\frac{x^{2}}{1+x^{6}}dx
Let I=\int _{0}^{\pi }\frac{\cos \left ( 2\theta \right ) }{5+4\cos \theta }d\theta Since the integrand is even then I=\frac{1}{2}\int _{-\pi }^{\pi }\frac{\cos \left ( 2\theta \right ) }{5+4\cos \theta }d\theta Let I_{1}=\int _{-\pi }^{\pi }\frac{\cos \left ( 2\theta \right ) }{5+4\cos \theta }d\theta , hence I=\frac{1}{2}I_{1} Now we evaluate I_{1}. Let z=re^{i\theta }, and for a unit circle, r=1, hence dz=ie^{i\theta }d\theta or d\theta =-i\frac{dz}{e^{i\theta }}=-i\frac{dz}{z}. Now we need to convert the integrand from function of \theta to function of z.
\cos \left ( 2\theta \right ) =\frac{e^{i2\theta }+e^{-i2\theta }}{2}=\frac{1}{2}\left ( z^{2}+z^{-2}\right ) and \cos \theta =\frac{e^{i\theta }+e^{-i\theta }}{2}=\frac{1}{2}\left ( z+z^{-1}\right ) , therefore the integral becomes I_{1}=\operatorname{Re}\oint \frac{\frac{1}{2}\left ( z^{2}+z^{-2}\right ) }{5+4\left ( \frac{1}{2}\left ( z+z^{-1}\right ) \right ) }\left ( -i\frac{dz}{z}\right ) The contour is over the unit circle. Let I_{2}=\oint \frac{\frac{1}{2}\left ( z^{2}+z^{-2}\right ) }{5+4\left ( \frac{1}{2}\left ( z+z^{-1}\right ) \right ) }\left ( -i\frac{dz}{z}\right ) \,, hence I_{1}=\operatorname{Re}\left ( I_{2}\right ) and now we evaluate I_{2}. \begin{align*} I_{2} & =\oint \frac{\frac{1}{2}\left ( z^{2}+z^{-2}\right ) }{5+4\left ( \frac{1}{2}\left ( z+z^{-1}\right ) \right ) }\left ( -i\frac{dz}{z}\right ) \\ & =-\frac{i}{2}\oint \frac{z^{2}+z^{-2}}{5+2\left ( z+z^{-1}\right ) }\frac{dz}{z}\\ & =-\frac{i}{2}\oint \frac{\frac{z^{4}+1}{z^{2}}}{5+2\left ( \frac{z^{2}+1}{z}\right ) }\frac{dz}{z}\\ & =-\frac{i}{2}\oint \frac{\frac{z^{4}+1}{z^{2}}}{\frac{5z+2\left ( z^{2}+1\right ) }{z}}\frac{dz}{z}\\ & =-\frac{i}{2}\oint \frac{z^{4}+1}{5z^{2}+2z\left ( z^{2}+1\right ) }\frac{dz}{z}\\ & =-\frac{i}{2}\oint \frac{z^{4}+1}{5z^{3}+2z^{2}\left ( z^{2}+1\right ) }dz\\ & =-\frac{i}{2}\oint \frac{z^{4}+1}{5z^{3}+2z^{4}+2z^{2}}dz\\ & =-\frac{i}{2}\oint \frac{z^{4}+1}{z^{2}\left ( 2z^{2}+5z+2\right ) }dz\\ & =-\frac{i}{4}\oint \frac{z^{4}+1}{z^{2}\left ( z^{2}+\frac{5}{2}z+1\right ) }dz\\ & =-\frac{i}{4}\oint \frac{z^{4}+1}{z^{2}\left ( z+2\right ) \left ( z+\frac{1}{2}\right ) }dz \end{align*}
The poles are z=0 of order 2 and z=-2 and z=-\frac{1}{2}, hence only z=-\frac{1}{2} is inside the unit circle. Lets find the residues of each now. \begin{align*} \text{residue}\left ( z=0\right ) & =\lim _{z\rightarrow 0}\frac{1}{\left ( 2-1\right ) !}\frac{d}{dz}\left ( z^{2}f\left ( z\right ) \right ) =\frac{d}{dz}\left ( \frac{z^{4}+1}{\left ( z+2\right ) \left ( z+\frac{1}{2}\right ) }\right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{2}{\left ( 2z^{2}+5z+2\right ) ^{2}}\left ( 4z^{5}+15z^{4}+8z^{3}-4z-5\right ) \right ) \\ & =\left ( \frac{2}{\left ( 2\right ) ^{2}}\left ( -5\right ) \right ) =-\frac{5}{2} \end{align*}
And\begin{align*} \text{residue}\left ( z=-\frac{1}{2}\right ) & =\lim _{z\rightarrow -\frac{1}{2}}\left ( \left ( z+\frac{1}{2}\right ) f\left ( z\right ) \right ) =\lim _{z\rightarrow -\frac{1}{2}}\left ( \frac{z^{4}+1}{z^{2}\left ( z+2\right ) }\right ) \\ & =\frac{\left ( -\frac{1}{2}\right ) ^{4}+1}{\left ( -\frac{1}{2}\right ) ^{2}\left ( -\frac{1}{2}+2\right ) }\\ & =\frac{17}{6} \end{align*}
Hence \begin{align*} \oint \frac{z^{4}+1}{z^{2}\left ( z+2\right ) \left ( z+\frac{1}{2}\right ) }dz & =2\pi i\left ( -\frac{5}{2}+\frac{17}{6}\right ) \\ & =\frac{2}{3}i\pi \end{align*}
Hence\begin{align*} -\frac{i}{4}\oint \frac{z^{4}+1}{z^{2}\left ( z+2\right ) \left ( z+\frac{1}{2}\right ) }dz & =\left ( -\frac{i}{4}\right ) \frac{2}{3}i\pi \\ & =\left ( \frac{1}{4}\right ) \frac{2}{3}\pi \\ & =\frac{1}{6}\pi \end{align*}
Hence I_{2}=\frac{1}{6}\pi But I_{1}=\operatorname{Re}\left ( I_{2}\right ) , hence I_{1}=\frac{1}{3}\pi . And I=\frac{1}{2}I_{1}, hence I=\frac{1}{12}\pi
I=\int _{0}^{2\pi }\frac{\sin ^{2}\theta }{a+b\cos \theta }d\theta where 0<b<a.
We need to convert this to contour integral over the unit circle. Let z=re^{i\theta }, and for a unit circle, r=1, hence dz=ie^{i\theta }d\theta or d\theta =-i\frac{dz}{e^{i\theta }}=-i\frac{dz}{z}. Now we need to convert the integrand from function of \theta to function of z.
\cos \left ( \theta \right ) =\frac{e^{i\theta }+e^{-i\theta }}{2}=\frac{1}{2}\left ( z+z^{-1}\right ) and \sin \theta =\frac{e^{i\theta }-e^{-i\theta }}{2i}=\frac{1}{2i}\left ( z-z^{-1}\right ) , Hence \begin{align*} \sin ^{2}\theta & =\left ( \frac{1}{2i}\left ( z-z^{-1}\right ) \right ) ^{2}\\ & =\frac{-1}{4}\left ( z-z^{-1}\right ) ^{2}=\frac{-1}{4}\left ( z^{2}+z^{-2}-2\right ) \end{align*}
Therefore the integral becomes\begin{align*} I & =\oint \frac{\frac{-1}{4}\left ( z^{2}+z^{-2}-2\right ) }{a+b\frac{1}{2}\left ( z+z^{-1}\right ) }\left ( -i\frac{dz}{z}\right ) \\ & =\frac{i}{4}\oint \frac{z^{2}+z^{-2}-2}{a+b\frac{1}{2}\left ( \frac{z^{2}+1}{z}\right ) }\frac{dz}{z}\\ & =\frac{i}{4}\oint \frac{\frac{z^{4}+1-2z^{2}}{z^{2}}}{az+b\frac{1}{2}\left ( z^{2}+1\right ) }dz\\ & =\frac{i}{2}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{2az+b\left ( z^{2}+1\right ) }dz\\ & =\frac{i}{2}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{bz^{2}+2az+b}dz\\ & =\frac{i}{2b}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{z^{2}+\frac{2a}{b}z+1}dz \end{align*}
Roots of z^{2}+\frac{2a}{b}z+1 are \frac{-b\pm \sqrt{b^{2}-4ac}}{2a}=\frac{-\frac{2a}{b}\pm \sqrt{\left ( \frac{2a}{b}\right ) ^{2}-4}}{2}=-\frac{a}{b}\pm \frac{1}{2}\sqrt{\frac{4a^{2}}{b^{2}}-4}=-\frac{a}{b}\pm \sqrt{\left ( \frac{a}{b}\right ) ^{2}-1} Hence r_{1}=-\frac{a}{b}-\sqrt{\left ( \frac{a}{b}\right ) ^{2}-1} and r_{2}=-\frac{a}{b}+\sqrt{\left ( \frac{a}{b}\right ) ^{2}-1} Since a>b then r_{1} is outside the unit circle. but r_{2} is inside. The integral is now I=\frac{i}{2b}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{\left ( z-r_{1}\right ) \left ( z-r_{2}\right ) }dz pole at z=0 or order 2. To find the residue for this pole\begin{align*} res\left ( z=0\right ) & =\lim _{z\rightarrow 0}\frac{1}{\left ( 2-1\right ) !}\left ( z^{2}f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{z^{4}-2z^{2}+1}{\left ( z-r_{1}\right ) \left ( z-r_{2}\right ) }\right ) \\ & =\frac{1}{\left ( -r_{1}\right ) \left ( -r_{2}\right ) }\\ & =\frac{1}{r_{1}r_{2}} \end{align*}
To find the residue for this r_{2}\begin{align*} res\left ( z=r_{2}\right ) & =\lim _{z\rightarrow r_{2}}\left ( \left ( z-r_{2}\right ) f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow r_{2}}\left ( \frac{z^{4}-2z^{2}+1}{z^{2}\left ( z-r_{1}\right ) }\right ) \\ & =\frac{r_{2}^{4}-2r_{2}^{2}+1}{r_{2}^{2}\left ( r_{2}-r_{1}\right ) } \end{align*}
Therefore, \begin{align*} I & =\frac{i}{2b}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{z^{2}+\frac{2a}{b}z+1}dz\\ & =\frac{i}{2b}\left ( 2\pi i\left ( \frac{1}{r_{1}r_{2}}+\frac{r_{2}^{4}-2r_{2}^{2}+1}{r_{2}^{2}\left ( r_{2}-r_{1}\right ) }\right ) \right ) \\ & =\frac{-\pi }{b}\left ( \frac{1}{r_{1}r_{2}}+\frac{r_{2}^{4}-2r_{2}^{2}+1}{r_{2}^{2}\left ( r_{2}-r_{1}\right ) }\right ) \end{align*}
This is the value of the integral, where r_{1},r_{2} are given as above. To simplify this final result, CAS was used for this step\begin{align*} I & =\frac{-\pi }{b}\left ( \frac{1}{\left ( -\frac{a}{b}-\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) \left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) }+\frac{\left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) ^{4}-2\left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) ^{2}+1}{\left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) \left ( \left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) -\left ( -\frac{a}{b}-\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) \right ) }\right ) \\ & =-\frac{\pi }{b}\left ( 1+\frac{2\sqrt{\left ( a-b\right ) \left ( a+b\right ) }}{b}\right ) \\ & =-\frac{\pi }{b}\left ( 1+\frac{2\sqrt{a^{2}-b^{2}}}{b}\right ) \end{align*}
Therefore I=\left ( \frac{-b-2\sqrt{a^{2}-b^{2}}}{b^{2}}\right ) \pi
I=\int _{-\infty }^{\infty }\frac{x^{2}}{1+x^{6}}dx
We first need to determine if the integral over the upper half plan vanish when R\rightarrow \infty , and for this we just need to show that \lim _{z\rightarrow \infty }zf\left ( z\right ) =0 where f\left ( z\right ) =\frac{z^{2}}{1+z^{6}} Hence\begin{align*} \lim _{z\rightarrow \infty }zf\left ( z\right ) & =\lim _{z\rightarrow \infty }\left ( z\frac{z^{2}}{1+z^{6}}\right ) \\ & =\lim _{z\rightarrow \infty }\left ( \frac{z^{3}}{1+z^{6}}\right ) =\lim _{z\rightarrow \infty }\left ( \frac{1}{\frac{1}{z^{3}}+z^{3}}\right ) =\frac{1}{0+\infty }=0 \end{align*}
Hence the integral becomes I=\int _{-\infty }^{\infty }\frac{z^{2}}{1+z^{6}}dz=2\pi i\sum \limits ^{UHP}res\left ( f\left ( z\right ) \right ) Now need to find the poles in UHP. From f\left ( z\right ) =\frac{z^{2}}{1+z^{6}} the poles are the roots of 1+z^{6}=0 or z^{6}=-1, therefore z=-1^{\left ( \frac{1}{6}\right ) }, but -1=e^{i\pi } Hence need to spread 6 poles around 2\pi , which means the phase changes by \frac{2\pi }{6} between each, hence \begin{align*} z & =\left \{ e^{i\frac{\pi }{6}},e^{i\frac{\pi }{6}+\frac{2\pi }{6}},e^{i\frac{\pi }{6}+\frac{4\pi }{6}},e^{i\frac{\pi }{6}+\frac{6\pi }{6}},e^{i\frac{\pi }{6}+\frac{8\pi }{6}},e^{i\frac{\pi }{6}+\frac{10\pi }{6}}\right \} \\ & =\left \{ e^{i\frac{\pi }{6}},e^{i\frac{3\pi }{6}},e^{i\frac{5\pi }{6}},e^{i\frac{7\pi }{6}},e^{i\frac{9\pi }{6}},e^{i\frac{11\pi }{6}}\right \} \end{align*}
Now need to find which of these roots is in UHP. Looking at the phase, we see that e^{i\frac{\pi }{6}},e^{i\frac{3\pi }{6}},e^{i\frac{5\pi }{6}} are in UHP since phase is less than \pi . So now we need to find residue at each pole. I=2\pi i\left ( res\left ( e^{i\frac{\pi }{6}}\right ) +res\left ( e^{i\frac{\pi }{2}}\right ) +res\left ( e^{i\frac{5\pi }{6}}\right ) \right ) Using \left [ \frac{N\left ( z\right ) }{D^{\prime }\left ( z\right ) }\right ] _{z->z_{o}} to find residue at z=z_{0} (since each is a simple pole). But D^{\prime }\left ( z\right ) =\frac{d}{dz}\left ( 1+z^{6}\right ) =6z^{5}, hence\begin{align*} res\left ( e^{i\frac{\pi }{6}}\right ) & =\left ( \frac{z^{2}}{6z^{5}}\right ) _{z=e^{i\frac{\pi }{6}}}\\ & =\frac{e^{i\frac{2\pi }{6}}}{6e^{i\frac{5\pi }{6}}}=\frac{e^{i\left ( \frac{2\pi }{6}-\frac{5\pi }{6}\right ) }}{6}=\frac{1}{6}e^{i\frac{-\pi }{2}}=\frac{-i}{6} \end{align*}
And\begin{align*} res\left ( e^{i\frac{3\pi }{6}}\right ) & =\left ( \frac{z^{2}}{6z^{5}}\right ) _{z=e^{i\frac{3\pi }{6}}}\\ & =\frac{e^{i\frac{6\pi }{6}}}{6e^{i\frac{15\pi }{6}}}=\frac{e^{i\left ( \frac{6\pi }{6}-\frac{15\pi }{6}\right ) }}{6}=\frac{1}{6}e^{i\frac{-9\pi }{6}}=\frac{1}{6}e^{-i\frac{3}{2}\pi }=\frac{i}{6} \end{align*}
And\begin{align*} res\left ( e^{i\frac{5\pi }{6}}\right ) & =\left ( \frac{z^{2}}{6z^{5}}\right ) _{z=e^{i\frac{5\pi }{6}}}\\ & =\frac{e^{i\frac{10\pi }{6}}}{6e^{i\frac{25\pi }{6}}}=\frac{e^{i\left ( \frac{10\pi }{6}-\frac{25\pi }{6}\right ) }}{6}=\frac{1}{6}e^{i\frac{-15\pi }{6}}=\frac{1}{6}e^{-i\frac{\pi }{2}}=\frac{-i}{6} \end{align*}
Therefore\begin{align*} I & =2\pi i\left ( res\left ( e^{i\frac{\pi }{6}}\right ) +res\left ( e^{i\frac{\pi }{2}}\right ) +res\left ( e^{i\frac{5\pi }{6}}\right ) \right ) \\ & =2\pi i\left ( \frac{-i}{6}+\frac{i}{6}-\frac{i}{6}\right ) \end{align*}
Hence I=\frac{\pi }{3}
Evaluate the following integration by integrating around a suitably indented contour in the complex plane I=\int _{0}^{\infty }\frac{\sin \left ( ax\right ) }{x\left ( x^{2}+b^{2}\right ) }dx where a>0, b>0
Solution\begin{align*} I & =\frac{1}{2}\int _{-\infty }^{\infty }\frac{\sin \left ( ax\right ) }{x\left ( x^{2}+b^{2}\right ) }dx\\ & =\frac{1}{2}\operatorname{Im}\left ( \int _{-\infty }^{\infty }\frac{e^{iaz}}{z\left ( z^{2}+b^{2}\right ) }dz\right ) \\ & =\frac{1}{2}\operatorname{Im}\left ( \int _{-\infty }^{\infty }\frac{e^{iaz}}{z\left ( z-ib\right ) \left ( z+ib\right ) }dz\right ) \end{align*}
To show that the UHP integral vanish we need to show that \lim _{\left \vert z\right \vert \rightarrow \infty }zf\left ( z\right ) =0 then we can just do the integration over the real line using residues of poles in UHP. \lim _{\left \vert z\rightarrow \infty \right \vert }\left ( z\frac{e^{iaz}}{z\left ( z^{2}+b^{2}\right ) }\right ) =\lim _{\left \vert z\rightarrow \infty \right \vert }\left ( \frac{e^{iaz}}{z^{2}+b^{2}}\right ) \rightarrow 0 Since \left \vert e^{iaz}\right \vert =1. The poles at the real line are z=0 and poles in complex plane are z=-ib and z=ib. Since b>0 then z=ib is only in UHP. I=\frac{1}{2}\operatorname{Im}\left ( \pi i\left [ res\left ( 0\right ) \right ] +2\pi i\left [ res\left ( ib\right ) \right ] \right ) To find residue at z=0, using res\left ( 0\right ) =\lim _{z\rightarrow 0}\left ( z\frac{e^{iaz}}{z\left ( z^{2}+b^{2}\right ) }\right ) =\lim _{z\rightarrow 0}\left ( \frac{e^{iaz}}{\left ( z^{2}+b^{2}\right ) }\right ) =\frac{1}{b^{2}} And res\left ( ib\right ) =\lim _{z\rightarrow ib}\left ( \left ( z-ib\right ) \frac{e^{iaz}}{z\left ( z-ib\right ) \left ( z+ib\right ) }\right ) =\lim _{z\rightarrow ib}\left ( \frac{e^{iaz}}{z\left ( z+ib\right ) }\right ) =\frac{e^{-ab}}{-2b^{2}} Therefore\begin{align*} I & =\frac{1}{2}\operatorname{Im}\left ( \pi i\left [ \frac{1}{b^{2}}\right ] +2\pi i\left [ \frac{e^{-ab}}{-2b^{2}}\right ] \right ) \\ & =\frac{1}{2}\left ( \pi \left [ \frac{1}{b^{2}}\right ] +2\pi \left [ \frac{e^{-ab}}{-2b^{2}}\right ] \right ) \\ & =\frac{1}{2}\left ( \frac{\pi }{b^{2}}-\frac{\pi e^{-ab}}{b^{2}}\right ) \end{align*}
Hence I=\frac{\pi -\pi e^{-ab}}{2b^{2}}
Evaluate the integrals (a) \int _{-\infty }^{\infty }\frac{e^{px}-e^{qx}}{1-e^{x}}dx where 0<p<1,0<q<1 (b) \int _{0}^{\infty }\frac{\ln \left ( x^{2}+1\right ) }{1+x^{2}}dx
Solution
I=\int _{-\infty }^{\infty }\frac{e^{px}-e^{qx}}{1-e^{x}}dx Break the integral into 2 and use the rectangle grid method to show that each leg of the integral vanish I=I_{1}-I_{2} Where\begin{align*} I_{1} & =\int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz\\ I_{2} & =\int _{-\infty }^{\infty }\frac{e^{qz}}{1-e^{z}}dz \end{align*}
Looking at I_{1} for now. \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz=\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz+\overset{leg1}{\overbrace{\int _{R}^{R+2\pi i}\frac{e^{pz}}{1-e^{z}}dz}}+\int _{R+2\pi i}^{-R+2\pi i}\frac{e^{pz}}{1-e^{z}}dz+\overset{leg2}{\overbrace{\int _{-R+2\pi i}^{-R}\frac{e^{pz}}{1-e^{z}}dz}} looking at leg1 integral, \int _{R}^{R+2\pi i}\frac{e^{pz}}{1-e^{z}}dz. Let z=2\pi it+R or t=\frac{z-R}{2\pi i}, hence dt=\frac{dz}{2\pi i}. When z=R,t=0 and when z=R+2\pi i,t=1, hence the integral for leg1 becomes \int _{0}^{1}\frac{e^{p\left ( 2\pi it+R\right ) }}{1-e^{2\pi it+R}}2\pi idt=2\pi i\int _{0}^{1}\frac{e^{p\left ( 2\pi it+R\right ) }}{1-e^{2\pi it+R}}dt Now we need to show that the above goes to zero as R goes to infinity. Writing the above as 2\pi i\int _{0}^{1}\frac{e^{p2\pi it}e^{pR}}{1-e^{2\pi it}e^{R}}dt=2\pi i\int _{0}^{1}\frac{e^{p2\pi it}}{e^{-pR}-e^{2\pi it}e^{R\left ( 1-p\right ) }}dt Now \lim _{R\rightarrow \infty }e^{-pR}=0 since p>0 and \lim _{R\rightarrow \infty }e^{R\left ( 1-p\right ) }=\infty since 1-p is positive, since p<1. Therefore the above becomes 2\pi i\int _{0}^{1}\frac{e^{p2\pi it}}{0-e^{2\pi it}\infty }dt And since \left \vert e^{ix}\right \vert =1 then the integrand becomes \frac{1}{-\infty }\rightarrow 0, hence the integral vanishes. We need to do the same for the second leg \int _{-R+2\pi i}^{-R}\frac{e^{pz}}{1-e^{z}}dz Let z=2\pi it+R or t=\frac{z+R}{2\pi i}, hence dt=\frac{dz}{2\pi i}. When z=-R,t=0 and when z=-R+2\pi i,t=1, hence the integral for leg2 becomes \int _{1}^{0}\frac{e^{p\left ( 2\pi it+R\right ) }}{1-e^{2\pi it+R}}2\pi idt=2\pi i\int _{1}^{0}\frac{e^{p\left ( 2\pi it+R\right ) }}{1-e^{2\pi it+R}}dt Now we need to show that the above goes to zero as R goes to infinity. Writing the above as 2\pi i\int _{0}^{1}\frac{e^{p2\pi it}e^{qR}}{1-e^{2\pi it}e^{R}}dt=2\pi i\int _{0}^{1}\frac{e^{p2\pi it}}{e^{-qR}-e^{2\pi it}e^{R\left ( 1-p\right ) }}dt Now \lim _{R\rightarrow \infty }e^{-pR}=0 since p>0 and \lim _{R\rightarrow \infty }e^{R\left ( 1-p\right ) }=\infty since 1-p is positive, since p<1. Therefore the above becomes 2\pi i\int _{0}^{1}\frac{e^{p2\pi it}}{0-e^{2\pi it}\infty }dt And since \left \vert e^{ix}\right \vert =1 then the integrand becomes \frac{1}{-\infty }\rightarrow 0, hence the integral vanishes. So we are left with these now \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz=\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz+\int _{R+2\pi i}^{-R+2\pi i}\frac{e^{pz}}{1-e^{z}}dz Now we use t=z-2\pi i for the top edge only. dt=dz, when z=R+2\pi i,t=R and when z=-R+2\pi i,t=-R, hence the above becomes\begin{align*} \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz+\int _{R}^{-R}\frac{e^{p\left ( t+2\pi i\right ) }}{1-e^{t}}dt\\ & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz-\int _{-R}^{R}\frac{e^{p\left ( t+2\pi i\right ) }}{1-e^{t}}dt\\ & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz-\int _{-R}^{R}\frac{e^{pt}e^{p2\pi i}}{1-e^{t}}dt\\ & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz-e^{p2\pi i}\int _{-R}^{R}\frac{e^{pt}}{1-e^{t}}dt\\ & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz-e^{p2\pi i}\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz\\ & =\left ( 1-e^{p2\pi i}\right ) \int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz \end{align*}
But in the limit \lim _{R\rightarrow \infty } \left ( 1-e^{p2\pi i}\right ) \int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz\rightarrow \left ( 1-e^{p2\pi i}\right ) \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz=2\pi i\sum res Hence \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz=\frac{1}{\left ( 1-e^{p2\pi i}\right ) }\left ( 2\pi i\sum ^{UHP}res+\pi i\sum ^{line}res\right ) Now we need to find poles in the rectangle. Poles of f\left ( z\right ) =\frac{e^{pz}}{1-e^{z}} are e^{z}=1, hence z=0,i2\pi ,i4\pi ,\cdots so only z=0 and z=i2\pi is of interest to use. The pole at z=0 is on the real line, so this get i\pi and the pole at i2\pi get i2\pi contribution. But res\left ( 2\pi i\right ) =\left [ \frac{N\left ( z\right ) }{D^{\prime }\left ( z\right ) }\right ] _{z=2\pi i}=\left [ \frac{e^{pz}}{-e^{z}}\right ] _{z=2\pi i}=\frac{e^{p2\pi i}}{-e^{2\pi i}}=-e^{p2\pi i} And res\left ( 0\right ) =\left [ \frac{N\left ( z\right ) }{D^{\prime }\left ( z\right ) }\right ] _{z=0}=\left [ \frac{e^{pz}}{-e^{z}}\right ] _{z=0}=-1 Hence\begin{align*} \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz & =\frac{1}{\left ( 1-e^{p2\pi i}\right ) }\left ( 2\pi i\left ( -e^{p2\pi i}\right ) +\pi i\left ( -1\right ) \right ) \\ & =\frac{-2\pi ie^{2\pi ip}-\pi i}{\left ( 1-e^{p2\pi i}\right ) }\\ & =\pi i\left ( \frac{-2e^{2\pi ip}-1}{1-e^{p2\pi i}}\right ) \end{align*}
For I_{2}, the result will be similar, hence I_{2}=\pi i\left ( \frac{-2e^{2\pi iq}-1}{1-e^{q2\pi i}}\right ) Hence\begin{align*} I & =I_{1}-I_{2}\\ & =\pi i\left ( \frac{-2e^{2\pi ip}-1}{1-e^{p2\pi i}}\right ) -\pi i\left ( \frac{-2e^{2\pi iq}-1}{1-e^{q2\pi i}}\right ) \\ & =\pi i\left ( \frac{-2e^{2\pi ip}-1}{1-e^{p2\pi i}}-\frac{-2e^{2\pi iq}-1}{1-e^{q2\pi i}}\right ) \end{align*}
I=\int _{0}^{\infty }\frac{\ln \left ( x^{2}+1\right ) }{1+x^{2}}dx parameterize it as I\left ( a\right ) =\int _{0}^{\infty }\frac{\ln \left ( ax^{2}+1\right ) }{1+x^{2}}dx Differentia w.r.t. a\begin{align*} I^{\prime }\left ( a\right ) & =\int _{0}^{\infty }\frac{d}{da}\frac{\ln \left ( ax^{2}+1\right ) }{1+x^{2}}dx\\ & =\int _{0}^{\infty }\frac{x^{2}}{\left ( 1+x^{2}\right ) \left ( 1+ax^{2}\right ) }dx\\ & =\frac{1}{2}\int _{-\infty }^{\infty }\frac{z^{2}}{\left ( 1+z^{2}\right ) \left ( 1+az^{2}\right ) }dz\\ & =\frac{1}{2a}\int _{-\infty }^{\infty }\frac{z^{2}}{\left ( 1+z^{2}\right ) \left ( \frac{1}{a}+z^{2}\right ) }dz\\ & =\frac{1}{2a}\int _{-\infty }^{\infty }\frac{z^{2}}{\left ( z-i\right ) \left ( z+i\right ) \left ( z-\frac{i}{\sqrt{a}}\right ) \left ( z+\frac{i}{\sqrt{a}}\right ) }dz \end{align*}
Poles are at z=\pm i and z=\pm \frac{i}{\sqrt{a}}. Pole z=\{i,\frac{i}{\sqrt{a}}\} are in UHP assuming a>0. Residue for z=i is\begin{align*} res\left ( i\right ) & =\lim _{z\rightarrow i}\frac{z^{2}}{\left ( z+i\right ) \left ( z-\frac{i}{\sqrt{a}}\right ) \left ( z+\frac{i}{\sqrt{a}}\right ) }\\ & =\frac{-1}{\left ( 2i\right ) \left ( i-\frac{i}{\sqrt{a}}\right ) \left ( i+\frac{i}{\sqrt{a}}\right ) }\\ & =-i\frac{a}{2a-2} \end{align*}
Residue for z=\frac{i}{\sqrt{a}}\begin{align*} res\left ( i\sqrt{a}\right ) & =\lim _{z\rightarrow \frac{i}{\sqrt{a}}}\frac{z^{2}}{\left ( z-i\right ) \left ( z+i\right ) \left ( z+\frac{i}{\sqrt{a}}\right ) }\\ & =\frac{\frac{-1}{a}}{\left ( \frac{i}{\sqrt{a}}-i\right ) \left ( \frac{i}{\sqrt{a}}+i\right ) \left ( \frac{i}{\sqrt{a}}+\frac{i}{\sqrt{a}}\right ) }\\ & =i\frac{\sqrt{a}}{2a-2} \end{align*}
Hence\begin{align*} \frac{1}{2a}\int _{-\infty }^{\infty }\frac{z^{2}}{\left ( z-i\right ) \left ( z+i\right ) \left ( z-\frac{i}{\sqrt{a}}\right ) \left ( z+\frac{i}{\sqrt{a}}\right ) }dz & =\frac{1}{2a}2\pi i\left ( -i\frac{a}{2a-2}+i\frac{\sqrt{a}}{2a-2}\right ) \\ & =\frac{1}{2}\frac{\pi }{a+\sqrt{a}} \end{align*}
Therefore I^{\prime }\left ( a\right ) =\frac{1}{2}\frac{\pi }{a+\sqrt{a}} Integrate\begin{align*} I\left ( a\right ) & =\frac{\pi }{2}\int \frac{1}{a+\sqrt{a}}da\\ & =\frac{\pi }{2}2\log \left ( \sqrt{a}+1\right ) +C\\ & =\pi \log \left ( \sqrt{a}+1\right ) +C \end{align*}
To find C, from I\left ( a\right ) =\int _{0}^{\infty }\frac{\ln \left ( ax^{2}+1\right ) }{1+x^{2}}dx we see that at a=0 then I\left ( 0\right ) =0\,\ hence\begin{align*} 0 & =\pi \log \left ( 0+1\right ) +C\\ C & =0 \end{align*}
Hence I\left ( a\right ) =\pi \log \left ( \sqrt{a}+1\right ) To obtain the integral we started with, let a=1, hence\begin{align*} I\left ( 1\right ) & =\int _{0}^{\infty }\frac{\ln \left ( x^{2}+1\right ) }{1+x^{2}}dx\\ & =\left [ \pi \log \left ( \sqrt{a}+1\right ) \right ] _{a=1}\\ & =\pi \log \left ( 1+1\right ) \end{align*}
Hence \int _{0}^{\infty }\frac{\ln \left ( x^{2}+1\right ) }{1+x^{2}}dx=\pi \log \left ( 2\right )
Determine the Laplace inversion for (a) F\left ( s\right ) =\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) } (b)F\left ( s\right ) =\frac{1}{\left ( a+b\right ) \cosh \left ( a\sqrt{s}\right ) }
Using Bromwich formula\begin{align*} f\left ( t\right ) & =\frac{1}{2\pi i}\lim _{b\rightarrow \infty }\int _{a-ib}^{a+ib}F\left ( s\right ) e^{st}ds\\ & =\frac{1}{2\pi i}\lim _{b\rightarrow \infty }\int _{a-ib}^{a+ib}\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }e^{st}ds \end{align*}
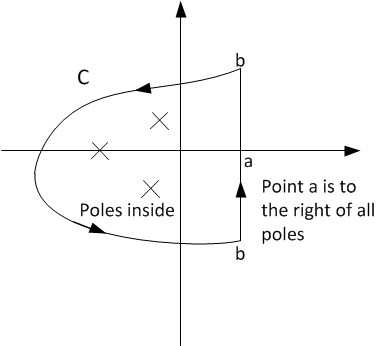
The integral is broken into 2 parts, the vertical leg and the integration of the curve shown above labeled C. f\left ( t\right ) =\frac{1}{2\pi i}\lim _{b\rightarrow \infty }\left ( \int _{a-ib}^{a+ib}\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }e^{st}ds+\oint \limits _{C}\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }e^{st}ds\right ) We can use the residue theorem on the above integral, but provided the function F\left ( s\right ) e^{st} is analytic inside the curve shown above (except of course at the poles, if any, inside the curve). Proof that F\left ( s\right ) e^{st} satisfies this condition is hence assumed. The proof was not given in class. So we need to calculate the residues of F\left ( s\right ) e^{st} for all the poles. f\left ( t\right ) =\frac{1}{2\pi i}\left ( 2\pi i\sum \limits _{i=1}^{poles}res\left ( F\left ( s_{i}e^{s_{i}t}\right ) \right ) \right ) So let us find the poles and the residue of each. Given \frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }e^{st}=\frac{s+1}{s^{2}\left ( s-\left ( -\frac{1}{2}i\sqrt{3}-\frac{1}{2}\right ) \right ) \left ( s-\left ( \frac{1}{2}i\sqrt{3}-\frac{1}{2}\right ) \right ) }e^{st} hence the poles are s=0 or order 2 and s_{1}=\left ( -\frac{1}{2}i\sqrt{3}-\frac{1}{2}\right ) and s_{2}=\left ( \frac{1}{2}i\sqrt{3}-\frac{1}{2}\right ) .
Residue for s=0 is \begin{align*} res\left ( 0\right ) & =\lim _{s\rightarrow 0}\frac{d}{ds}\left ( \frac{s^{2}\left ( s+1\right ) }{s^{2}\left ( s-s_{1}\right ) \left ( s-s_{2}\right ) }e^{st}\right ) \\ & =\lim _{s\rightarrow 0}\frac{d}{ds}\left ( \frac{\left ( s+1\right ) }{\left ( s-s_{1}\right ) \left ( s-s_{2}\right ) }e^{(st)}\right ) \\ & =t \end{align*}
And\begin{align*} res\left ( s_{1}\right ) & =\lim _{s\rightarrow s_{1}}\frac{\left ( s+1\right ) }{s^{2}\left ( s-s_{2}\right ) }e^{st}\\ & =-\frac{ie^{-\frac{1}{2}\left ( 1+i\sqrt{3}\right ) t}}{\sqrt{3}} \end{align*}
And\begin{align*} res\left ( s_{2}\right ) & =\lim _{s\rightarrow s_{2}}\frac{\left ( s+1\right ) }{s^{2}\left ( s-s_{1}\right ) }e^{st}\\ & =-\frac{(-i+\sqrt{3})e^{\frac{1}{2}\left ( 1+i\sqrt{3}\right ) t}}{3i+\sqrt{3}} \end{align*}
Therefore,\begin{align*} f\left ( t\right ) & =t-\frac{ie^{-\frac{1}{2}\left ( 1+i\sqrt{3}\right ) t}}{\sqrt{3}}-\frac{(-i+\sqrt{3})e^{\frac{1}{2}\left ( 1+i\sqrt{3}\right ) t}}{3i+\sqrt{3}}\\ & =t-\frac{2e^{-\frac{t}{2}}\sin \left ( \frac{\sqrt{3}t}{2}\right ) }{\sqrt{3}} \end{align*}
The setup is similar to part(a) and not will be repeated, we will go the step of finding the residues. For this, we need to first find the poles of F\left ( s\right ) e^{st}=\frac{e^{st}}{\left ( a+b\right ) \cosh \left ( a\sqrt{s}\right ) } The function \cosh \left ( x\right ) is zero at \pm \frac{i\pi }{2}+2i\pi n where n is the set of integers. For \cosh \left ( a\sqrt{s}\right ) this becomes -\frac{1}{4}\frac{\pi ^{2}}{a^{2}}\left ( 1+2n\right ) ^{2} for n integer. Hence, for n=0\begin{align*} res\left ( s\rightarrow \frac{-\pi ^{2}}{4a^{2}}\right ) & =\frac{1}{\left ( a+b\right ) }\lim _{s\rightarrow \frac{-\pi ^{2}}{4a^{2}}}\left ( s+\frac{\pi ^{2}}{4a^{2}}\right ) \frac{N\left ( s\right ) }{D^{\prime }\left ( s\right ) }\\ & =\frac{1}{\left ( a+b\right ) }\lim _{s\rightarrow \frac{-\pi ^{2}}{4a^{2}}}\frac{\left ( s+\frac{\pi ^{2}}{4a^{2}}\right ) 2\sqrt{s}e^{st}}{a\sinh \left ( a\sqrt{s}\right ) }\\ & =\frac{1}{\left ( a+b\right ) }\frac{\left ( 0\right ) 2\sqrt{\frac{-\pi ^{2}}{4a^{2}}}e^{\frac{-\pi ^{2}}{4a^{2}}t}}{a\sinh \left ( a\sqrt{\frac{-\pi ^{2}}{4a^{2}}}\right ) }\\ & =\frac{1}{\left ( a+b\right ) }\frac{\left ( 0\right ) 2\sqrt{\frac{-\pi ^{2}}{4a^{2}}}e^{\frac{-\pi ^{2}}{4a^{2}}t}}{a\sinh \left ( \frac{\pi i}{2}\right ) }\\ & =\frac{1}{\left ( a+b\right ) }\frac{\left ( 0\right ) 2\sqrt{\frac{-\pi ^{2}}{4a^{2}}}e^{\frac{-\pi ^{2}}{4a^{2}}t}}{ai}\\ & =0 \end{align*}
Hence the residue is zero. If we try for n=1,2,\cdots we’ll find all residues are zero. Hence\begin{align*} f\left ( t\right ) & =\frac{1}{2\pi i}\left ( 2\pi i\sum \limits _{i=1}^{poles}res\left ( s_{i}\right ) \right ) \\ & =0 \end{align*}
I have something wrong. Need more time to work on this.